知识点 - 确定有穷自动机

最新推荐文章于 2024-05-01 11:47:53 发布

Best KeyBoard

最新推荐文章于 2024-05-01 11:47:53 发布

阅读量1.6k

点赞数

CC 4.0 BY-SA版权

分类专栏：字符串

本文链接：https://blog.youkuaiyun.com/qq_41848675/article/details/99104373

字符串专栏收录该内容

6 篇文章

订阅专栏

本文介绍确定有穷自动机(DFA)的基本概念及其在字符串匹配和文本分析中的应用。通过实例解析了如何使用DFA判断二进制数是否为3的倍数，并详细阐述了解决字符矩阵旋转与翻转问题的算法思路。

知识点 - 确定有穷自动机 DFA Deterministic finite automaton

解决问题类型：

求字符矩阵进行1e6次旋转(2个方向)和翻转(4个方向)后的状态。

字符串匹配、文本分析。

定义

确定有穷自动机M由五个元素组成： $M=(Q，\Sigma，\delta，q_0，F)$ 其中

$Q ：$ 状态的集合；

$q_0:q_0\in Q$ 是唯一的初始状态；

$F:F\subseteq Q$ 是终止状态(accept state)集合。

$Σ ：$ 输入的字母表；

$\delta：$ 转换函数，是在 $Q \times Σ \to Q$ 上的映射.

e.g.判断二进制是否是3的倍数的自动机

0,11, 110, 1001, 1100, 1111, 10010, 10101, 11000, 11011, 11110, 100001, 100100, 100111, 101010, 101101, 110000, 110011, 110110, 111001, 111100, 111111,

在这里插入图片描述

状态是满足特定条件的二进制数,字母表是01。

每次读一个符号，DFA就确定地从一个状态转移到另一个状态。转移用箭头表示。

初始状态是 $S_0$ ,它被一个没有起点的箭头所指。

终止状态也是 $S_0$ ，它用两个圈表示。

复杂度：

$O (N + M)$ N是指令串的长度，M是单次转移的复杂度

例题

Rotating Display : 求一个字符矩阵进行1e6次旋转(< >2个方向)和翻转(- |/ \4个方向)后的状态。

我们只需要2个转移(比如|,<)就能实现所有操作，于是我们得到八种不同的状态，画出下面的图。

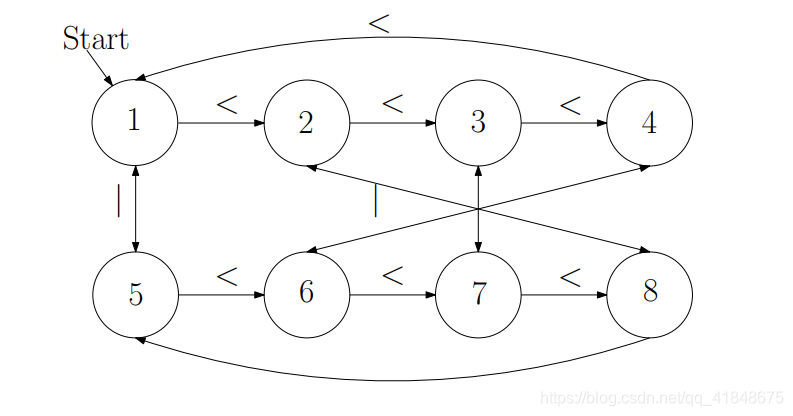
在这里插入图片描述

代码

/**
 * CTU Open 2016
 * Problem Solution: Display
 * 
 * @author Pavel Strnad
 */
 
#include <iostream>
#include <string>
#include <sstream>
#include <vector>
using namespace std;

// MxM
int M;
int state = 0;

vector<string> split(const char *str, char c = ' ')
{
    vector<string> result;
    do
    {
        const char *begin = str;
        while(*str != c && *str)
            str++;
        result.push_back(string(begin, str));
    } while (0 != *str++);
    return result;
}

void edgeRR() {
    state++;
    if(state == 4) state = 0;
    if(state == 15) state = 11;
}

void edgeRL() {
    state--;
    if(state == -1) state = 3;
    if(state == 10) state = 14;
}

void edgeFH() {
    switch(state) {
	case 0: state = 11; break;
	case 1: state = 14; break;
        case 2: state = 13; break;
        case 3: state = 12; break;
        case 11: state = 0; break;
        case 12: state = 3; break;
        case 13: state = 2; break;
        case 14: state = 1; break;
    }
}

char arr1[] = {'^','>','v','<'};
char arr2[] = {'/','\\', '/','\\'};
char arr3[] = {'|','-', '|','-'};

char getSymbolRL(char in) {
    for(int i = 0; i<4; i++) {
        int pos = (i-1)%4;
        pos = pos < 0 ? pos + 4 : pos;
	if(arr1[i] == in) {
	    return arr1[pos];
	}
	if(arr2[i] == in) {
	    return arr2[pos];
	}
	if(arr3[i] == in) {
	    return arr3[pos];
	}
    }
    return in;
}


char mh1[] = {'^','v'};
char mh2[] = {'/','\\'};

char getSymbolFH(char in) {
    for(int i = 0; i<2; i++) {
        int pos = (i-1)%2;
        pos = pos < 0 ? pos + 2 : pos;
	if(mh1[i] == in) {
	    return mh1[pos];
	}
	if(mh2[i] == in) {
	    return mh2[pos];
	}
    }
    return in;
}


void RL(char *d)
{
    for (int x = 0; x < M / 2; x++)
    {
        for (int y = x; y < M-x-1; y++)
        {
            // store current cell in temp variable
            char temp = getSymbolRL(*(d + x * (M + 1) + y));
 
            // move values from right to top
            *(d + x * (M + 1) + y) = getSymbolRL(*(d + y * (M + 1) + M-1-x));
 
            // move values from bottom to right
            *(d + y * (M + 1) + M-1-x) = getSymbolRL(*(d + (M-1-x) *(M+1) + M-1-y));
 
            // move values from left to bottom
            *(d + (M-1-x) * (M+1) + M-1-y) = getSymbolRL(*(d + (M-1-y) * (M+1) + x));
 
            // assign temp to left
            *(d + (M-1-y) * (M+1) + x) = temp;
        }
    }
    if(M%2==1) {
	*(d + (M/2) * (M+1) + M/2) = getSymbolRL(*(d + (M/2) * (M+1) + M/2));
    }
}

void FH(char *d) {
    for(int x = 0; x < M/2; x++) {
	for(int y = 0; y < M; y++) {
	    char temp = getSymbolFH(*(d + x * (M + 1) + y));
	    *(d + x * (M + 1) + y) = getSymbolFH(*(d + (M - 1 - x) * (M + 1) + y));
	    *(d + (M - 1 - x) * (M + 1) + y) = temp;	
	}
    }
    if(M%2==1) {
	for(int x = 0; x < M; x++) {
	    *(d + (M/2) * (M+1) + x) = getSymbolFH(*(d + (M/2) * (M+1) + x));
	}
    }

}

void transform(char *d) {
    switch(state) {
	case 0: return;
	case 1: RL(d);
	case 2: RL(d);
        case 3: RL(d); return;
        case 11: FH(d); return;
        case 12: FH(d); RL(d); RL(d); RL(d); return;
        case 13: FH(d); RL(d); RL(d); return;
        case 14: FH(d); RL(d); return;
	default: cout << "Unknown state" << endl;
    }
    return;
}

int main() {
    string line;
    while(getline(cin, line)) {
        state = 0;
	stringstream ss(line);
	ss >> M;
	char display[M][M+1];
	for(int i=0; i < M; i++) {
	    cin.getline(display[i],M+1);
	}
	getline(cin,line);
	for(string s : split(line.c_str())) {
	   if(s.compare("<")==0) {
		edgeRL();
	   }
	   if(s.compare(">")==0) {
		edgeRR();
	   }
	   if(s.compare("-")==0) {
		edgeFH();
	   }
	   if(s.compare("|")==0) {
		edgeFH(); edgeRR(); edgeRR();
	   }	   
	   if(s.compare("\\")==0) {
		edgeFH(); edgeRR();
	   }	   
	   if(s.compare("/")==0) {
		edgeFH(); edgeRL();
	   }	   
	}
	transform((char *) display);
	for(int i=0;i<M;i++) cout << display[i] << endl;
    }
    return 0;
}