UVA - 11809（打表）

最新推荐文章于 2022-01-11 15:16:22 发布

bug_killer@

最新推荐文章于 2022-01-11 15:16:22 发布

阅读量289

点赞数

CC 4.0 BY-SA版权

分类专栏：理论

本文链接：https://blog.youkuaiyun.com/qq_41829060/article/details/88095020

理论专栏收录该内容

66 篇文章

订阅专栏

本文探讨了计算机中浮点数的阶码-尾数存储方法，通过具体实例讲解了如何将十进制数AeB转换为二进制浮点数的阶码E和尾数M。利用对数特性，通过预计算表格来加速查找过程，实现高效转换。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题意：

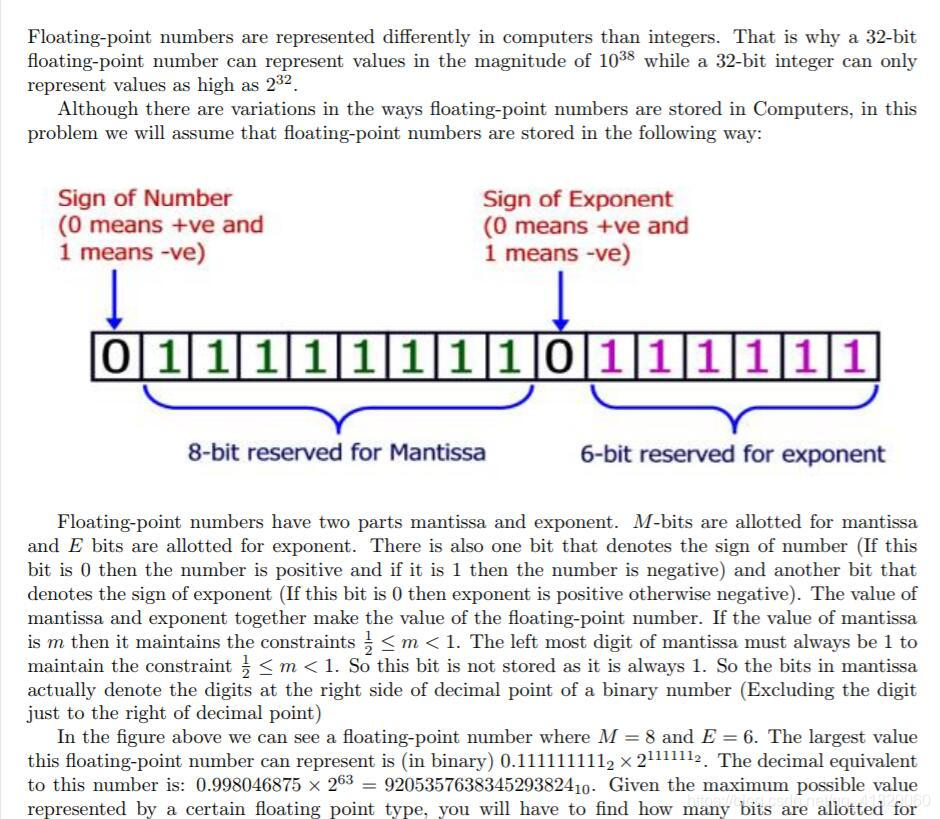
计算机采用阶码-尾数方法存储浮点数，如果阶码（E）有6位，尾数（M）有8位，最大可以表示的浮点数是

0.111 111 111（2）* 2^111 111（2），小数点后第一位必须为，保证m在0.5-1的范围内，所以一共有9位小数。

现在给出10进制的数字AeB，表示A*10^B，输出对应的M，E。

思路：

一开始不知道怎么做，参考了网上的文章，发现可以打表，因为M，E的范围都已经给出来了，

所以从0-9枚举M，1-30枚举E，然后转换为对应的A，B就好了，

但是数据太大回超限，所以需要特殊处理，对两遍去log10，

A*B^10 = C(2) * 2^d(2).

log10(A) + B = log10(C(2)) + d(2)*log10(2)

然后每次寻找表内最接近的值就好了。

参考文章

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
double ans[15][50]; //打表，枚举m在0-9,e在1-30范围内的最大数 
int main(void)
{
	double e,m,x;
	int i,c,d;
	char ss[550];
	for(c=0;c<=9;c++){
		for(d=1;d<=30;d++){
			m=1-pow(2,-1-c);//尾数 
			e=pow(2,d)-1; //指数 
			ans[c][d]=log10(m)+e*log10(2.0);
		}
	}
	while(1){
		scanf("%s",ss);
		for(i=0;ss[i];i++)
		if(ss[i]=='e'){
			ss[i]=' ';break;
		}
		sscanf(ss,"%lf %d",&m,&d);
		if(m==0&&d==0) break; //终止条件 
		x=log10(m)+d;
		int fg=0;
		for(c=0;c<=9;c++){
			for(d=1;d<=30;d++){
				if(fabs(ans[c][d]-x)<1e-5){
					printf("%d %d\n",c,d);fg=1;break;
				}
			}
			if(fg) break;
		}
	}
	return 0;
}