KNN算法以及cs231n代码实现

KNN算法

在介绍knn算法之前我们首先要对nn分类器有所了解，下面首先介绍nn分类器，在其中对一些基础知识进行介绍，之后介绍KNN算法，对于cs231n作业一中的knn完整可实现代码写于此。
数据集来源于http://www.cs.toronto.edu/~kriz/cifar.html，改数据集的具体信息可以在网上看到。在此便不进行叙述。

NN分类器

假设我们现在有一个关于狗的训练数据集，已经知道这些狗的品种，每个品种的狗有3种属性，为了方便起见，因此，这个数据集每个属性就是3-dim的，对应的我们可以在3维空间找到这个属性值对应的点。
如下图所示（楼主只接手绘了大家不要介意哈哈哈）：x，y，z分别代表着狗的一个属性，黑点就是一个狗的属性值在三维空间的位置。

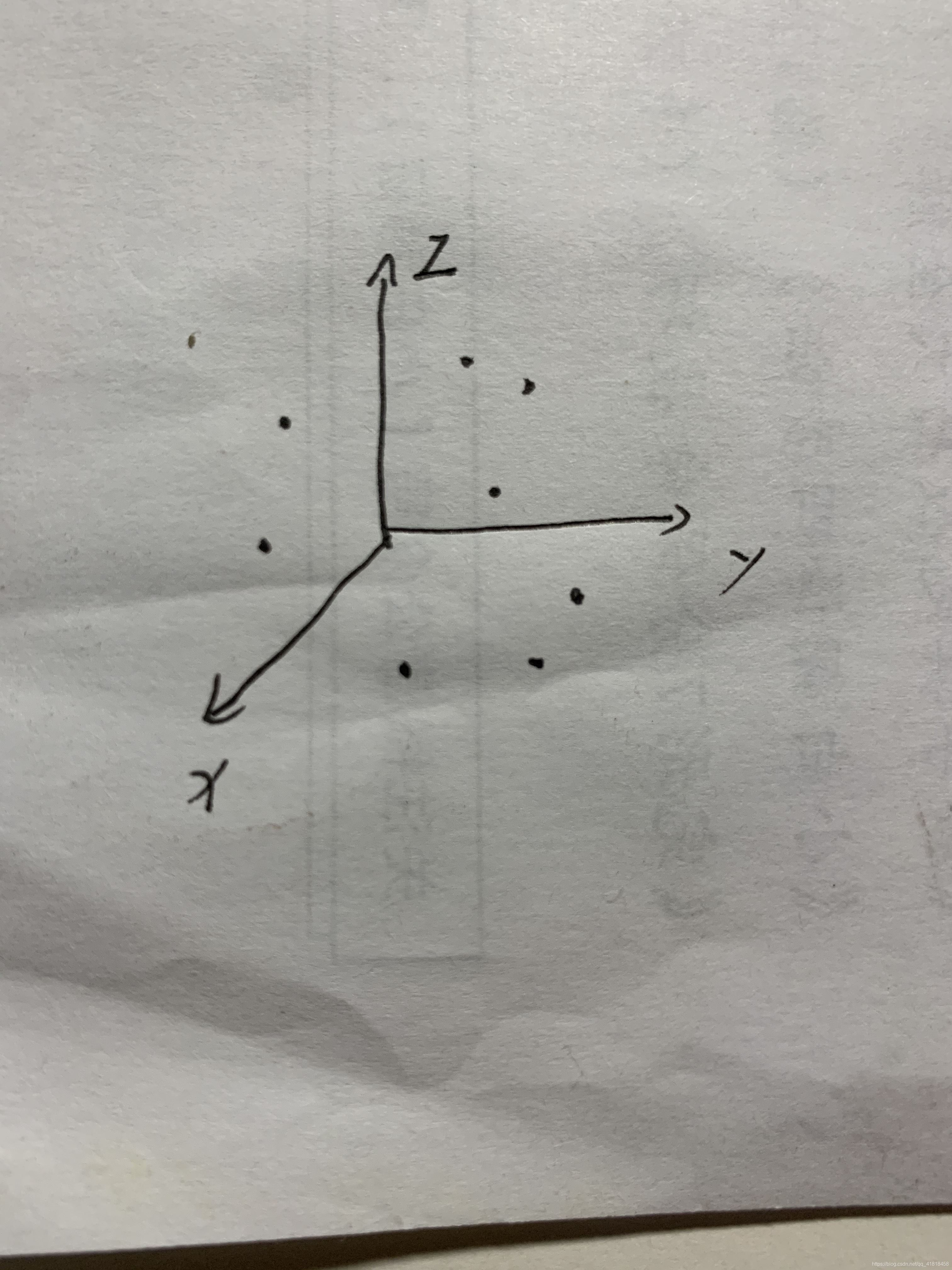
下图中的红点代表我们从测试集中随便找一个狗它的三个数据值在3维空间的位置，（测试集就是我们不知道它是什么品种的狗，我们想要通过分类器知道它是什么品种）。

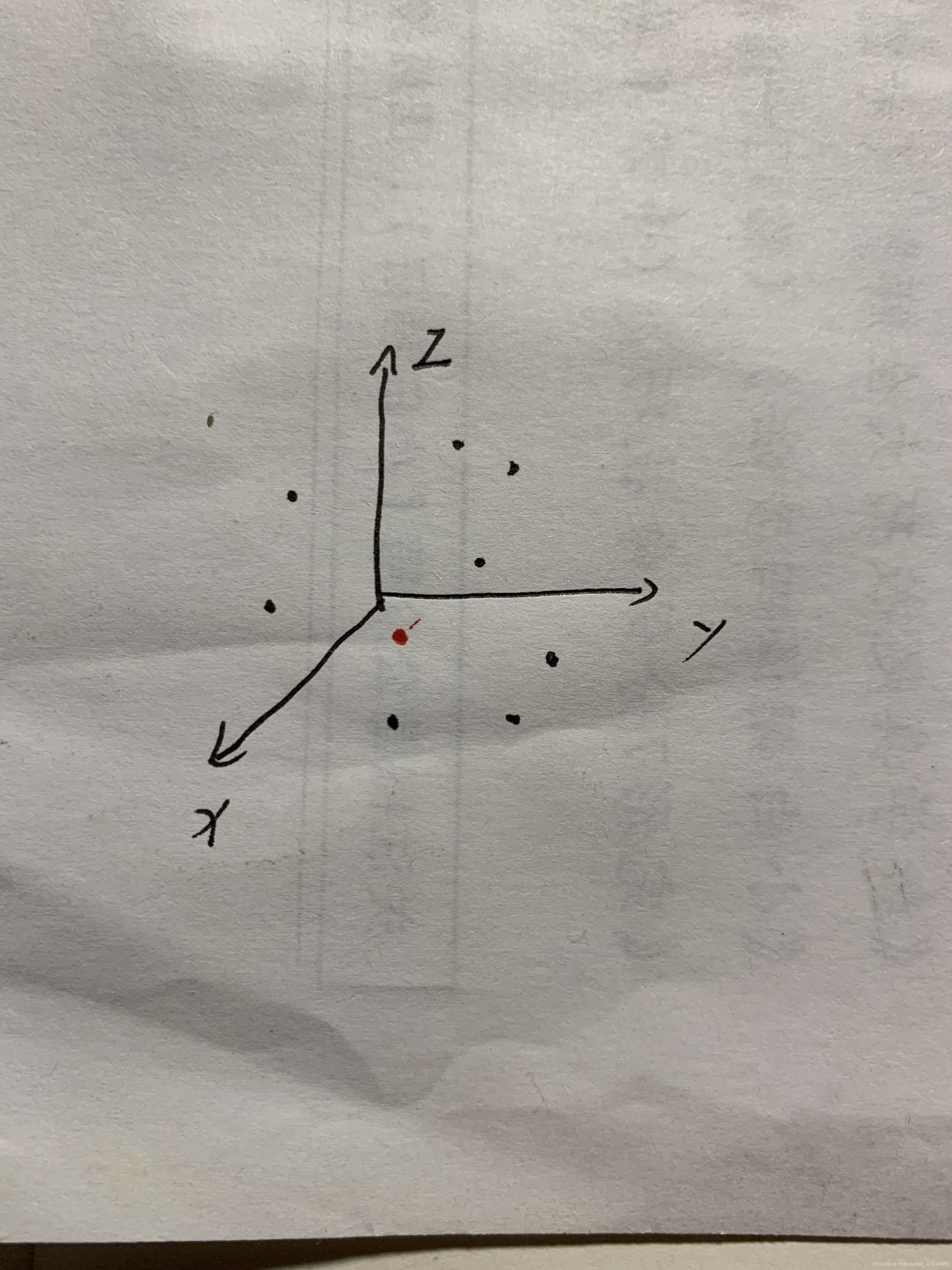
为了知道它属于什么品种的狗，我们将它分别与每个训练集中的狗的数据的距离计算出来，此处的距离有很多种含义，并非我们平常所理解的距离。L2距离才是我们理解的距离。
L1距离：$$d(I_1,I_2)=sum|I_1-I_2|$$
L2距离：
$$d(I_1,I_2)=sum\sqrt{(（I_1-I_2{）}^2)}$$
其中L1和L2均为向量而，sum即对减后的向量内的所有元素求和得到所谓的距离。

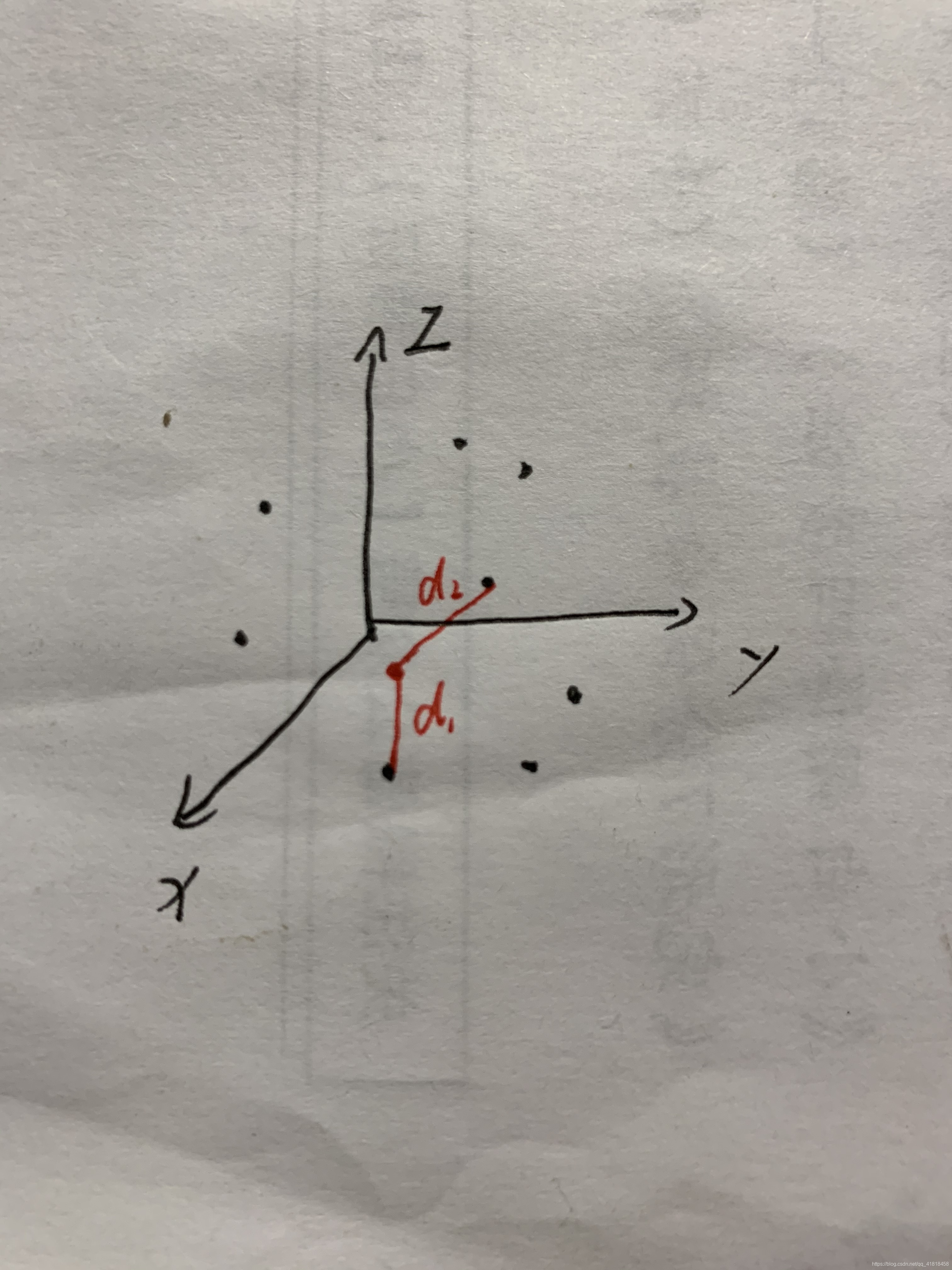
因此我们会得到d1,d2…等等距离数据。找到最近的一个也就是我们这个红点和哪个品种的狗最为接近了。

KNN算法介绍

上面我们已经了解了NN分类器，那么KNN又是什么意思呢，其实很简单，NN分类器我们可以看作K=1，KNN就是找距离最近的K个数据，然后从这K个数据中，看哪个品种出现的次数最多，那么我们测试选出的小红点就属于哪个品种了。计算距离的方法依旧不变。
K=1时未免太具有偶然性，这样可以降低判断出错的概率。
最后先奉上cs231n中NN的代码：

基于CIFAR-10NN分类器

// NN分类器
import numpy as np
import os
import pickle


def load_CIFAR_batch(filename):
    with open(filename, 'rb') as f:
        datadict = pickle.load(f, encoding='latin1')
    X = datadict['data']
    Y = datadict['labels']
    X = X.reshape(10000, 3, 32, 32).transpose(0, 2, 3, 1).astype("float")
    Y = np.array(Y)
    return X, Y


def load_CIFAR10(ROOT):
    xs = []
    ys = []
    for b in range(1, 6):
        f = os.path.join(ROOT, 'data_batch_%d' % (b))
        X, Y = load_CIFAR_batch(f)
        xs.append(X)
        ys.append(Y)
    Xtr = np.concatenate(xs)
    print(Xtr.shape)
    Ytr = np.concatenate(ys)
    del X, Y
    Xte, Yte = load_CIFAR_batch(os.path.join(ROOT, 'test_batch'))

    return Xtr, Ytr, Xte, Yte


class NearestNeighbor(object):
    def __init__(self):
        pass

    def train(self, X, Y):
        self.Xtr = X
        self.Ytr = Y

    def predict(self, X):
        num_test = X.shape[0]  # 预测数组大小
        Ypred=np.zeros(num_test,dtype=self.Ytr.dtype)
        for i in range(num_test):
            distance=np.sum(np.abs(self.Xtr-X[i,:]),axis=1)
            min_index=np.argmin(distance)
            Ypred[i]=self.Ytr[min_index]
        return Ypred

Xtr, Ytr, Xte, Yte = load_CIFAR10('D:/cs231n/DATA/cifar-10-batches-py') # a magic function we provide
# flatten out all images to be one-dimensional
print(Xte.shape)
Xtr_rows = Xtr.reshape(Xtr.shape[0], 32 * 32 * 3) # Xtr_rows becomes 50000 x 3072
Xte_rows = Xte.reshape(Xte.shape[0], 32 * 32 * 3)
nn=NearestNeighbor()
nn.train(Xtr_rows,Ytr)
Yte_predict=nn.predict()
print('accury:%f'%(np.mean(Yte_predict==Yte)))

基于CIFAR-10KNN分类器

// KNN
import numpy as np

class KNearestNeighbor(object):

    def __init__(self):
        pass

    def train(self, X, y):
        self.X_train = X
        self.y_train = y

    def predict(self, X, k=1, num_loops=0):
        if num_loops == 0:
            dists = self.compute_distances_no_loops(X)
        elif num_loops == 1:
            dists = self.compute_distances_one_loop(X)
        elif num_loops == 2:
            dists = self.compute_distances_two_loops(X)
        else:
            raise ValueError('Invalid value %d for num_loops' % num_loops)

        return self.predict_labels(dists, k=k)

    def compute_distances_two_loops(self, X):
        num_test = X.shape[0]
        num_train = self.X_train.shape[0]
        dists = np.zeros((num_test, num_train))
        for i in range(num_test):
            for j in range(num_train):
                diff = X[i] - self.X_train[j]  # (x1-y1, x2-y2, ... xd-yd)
                diff_2 = diff ** 2  # ((x1-y1)^2, (x2-y2)^2, ... (xd-yd)^2)
                d = np.sqrt(np.sum(diff_2))  # sqrt((x1-y1)^2 + (x2-y2)^2 + ... (xd-yd)^2)
                dists[i, j] = d
        return dists

    def compute_distances_one_loop(self, X):
        num_test = X.shape[0]
        num_train = self.X_train.shape[0]
        dists = np.zeros((num_test, num_train))
        for i in range(num_test):
            diff = self.X_train - X[i]  # 回忆一下什么是broadcast
            dist = np.sum(diff ** 2, axis=1)  #沿着行求和，即 (x1-y1)^2 + (x2-y2)^2 + ...
            dists[i, :] = np.sqrt(dist)  # 对平方和开根号
        return dists

    def compute_distances_no_loops(self, X):
        num_test = X.shape[0]
        num_train = self.X_train.shape[0]
        dists = np.zeros((num_test, num_train))
        # (x1 - y1)^2 + (x2 - y2)^2 = (x1^2 + x2^2) + (y1^2 + y2^2) - 2*(x1*y1 + x2*y2)
        train_sq = np.sum(self.X_train ** 2, axis=1, keepdims=True)  # (m, 1), 注意 keepdims 的含义
        train_sq = np.broadcast_to(train_sq, shape=(num_train, num_test)).T  # (n, m), 注意转置
        test_sq = np.sum(X ** 2, axis=1, keepdims=True)  # (n, 1)
        test_sq = np.broadcast_to(test_sq, shape=(num_test, num_train))  # (n, m)
        cross = np.dot(X, self.X_train.T)  # (n, m)
        dists = np.sqrt(train_sq + test_sq - 2 * cross)  # 开根号
        return dists

    def predict_labels(self, dists, k=1):

        num_test = dists.shape[0]
        y_pred = np.zeros(num_test)
        for i in range(num_test):
            closest_y = []
            test_dist = dists[i]  # 每个test样本和train set里面的距离
            sort_dist = np.argsort(test_dist)  # 得到排序下标，从小到大，即第一个下标表示最近的训练样本
            valid_idx = sort_dist[:k]  # 只取前k个
            closest_y = self.y_train[valid_idx]  # 获得前k个的label, 比如是 (1, 2, 2, 3)
            # 查看 np.unique 函数
            y_unique, y_count = np.unique(closest_y, return_counts=True)
            # 第一个是去掉closest_y中的重复元素，第二个是剩下的元素出现的次数
            common_idx = np.argmax(y_count)  # 出现次数最多的位置
            y_pred[i] = y_unique[common_idx]  # 取最大出现次数的label作为预测
        return y_pred

小结

本文算是笔者第一次写的经验总结了，有些功能用的还是不熟练，随着时间的流逝会越来越熟练的，希望大家多多捧场，多多鼓励谢谢大家！