【算法题】c/c++汇总大复习1-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_41775119/article/details/133852973

标题前面打*号的为多数考纲范围外的，可以选择性查看
🔗链接：严书代码大全
🔗链接：c/c++语言算法技巧汇总大复习1
🔗链接：c/c++语言算法技巧汇总大复习2

预处理

位段以二进制位为单位定义
struct status
{
Unsigned sign:1;
Unsigned zero:1;
}flags;

#define 宏名字符串（不是c语句，不需要在行末加分号）
#表示预处理命令不分配内存空间

条件编译：部分内容满足一定条件时才编译
#if 表达式为真
…
#endif

#if…
#elif…
#else…
#endif

循环妙用


for(auto &a:arr)
{
  std::cout << a;
}

1.拷贝str中的元素时：for(auto c:str);
2.修改str中的元素的时候：for(auto && x:str);
3.只读str中的元素的时候：for(const auto & x:str);

短路妙用

题目：求1+…+n 不能使用乘除、if…else\for\while\switch\case等关键字及条件判断语句(a?b:c)

class solution{
	public:
		int get_sum(int n){
			int res=n;
			n>=0 && (res+= get_sum(n-1));
			return res;
		}
}

妙用异或XOR

练习：只出现一次的数字

整数数组中只有一个元素出现了一次，找出它。
first=first ^ num[j];

枚举（暴力）

如果我们不满足于暴力解法，就应该想，暴力解法浪费了什么，我们在什么地方可以对他优化，优化一般要使时间或者空间复杂度减小（主要是时间复杂度），比如说题目给的是有序数组，但是我们没有用到有序性，这是有条件没用；或者题目不需要排序，只要求中位数，但是我们对他排序了，超额完成任务，本来可以不做这么多的，这就是浪费。最好的情况就是我们完美的利用了题目的条件，而且又不多做一丁点事，这样的算法一般都更优秀。
枚举emun color(red,green);//此时red=1,green=2，若还有元素则依次加1

练习：火柴棍等式

用n根(n<=24)火柴棍拼成A+B=C等式，能够有几种拼法？A,B,C均大于等于0，若该数非0则最高位不能是0.若A不等于B，则A+B=C B+A=C视为两种等式，所有火柴必须用上。等式和加号各需要两根火柴。数字0-9分别需要6,2,5,5,4,5,6,3,7,6根火柴。
思路：首先一个变量的取值范围是0～1111之间，如果得到A火柴数+B火柴数+C火柴数=n-4则为一种拼法，当然A+B=C，C不需要再枚举出来。

int fun(int x){
	int num=0;
	int f[10]={6,2,5,5,4,5,6,3,7,6};
	while(x/10!=0){
		num+=f(x%10);
		x/=10;
	}
	num+=fun(x);
	return num;
}
int main(){
	int a,b,c,m,sum=0;
	scanf("%d",&m);
	for(a=0;a<=1111;a++){
		for(b=0;b<=1111;b++){
			c=a+b;
			if(fun(a)+fun(b)+fun(c)==m-4)
			{
				printf("%d+%d=%d\n",a,b,c);
				sum++;
			}
		}
	}
	printf("%d kinds of equation",sum);
	return 0;
}

练习2:简单的全排列

几位就是几重循环判断条件是它们互不相等时输出

练习3:把一元钱兑换成1分，2分，5分的硬币，有多少种对法，编程输出所有方法

#include<stdio.h>
int main()
{
    int i,j;
    int sum=0;
    for(i=0;i<=50;i++)
	    for(j=0;j<=20;j++)
		    if(100-2*i-5*j>=0)
		    {
		        printf("1分%3d张  2分%3d张   5分%3d张",100-2*i-5*j,i,j);
		        sum++;
		        if(sum%2==0)
		            printf("\n"); //每三个为一行
		    }
    printf("\n%d\n",sum);
    return 0;
}

typedef是什么

typedef可理解成给现有的数据类型起一个新名字的意思。如typedef int a;就是将整型起了个新名字为a。

引用

指针变量引用

int &x放入形参，表示对指针x的引用
注意取指针的值的时候不可以用结构体用的“.”，而是“->”

数组的引用

注意：数组开小会显示“段错误”，改大之后就可以了

一维数组直接是int x[]；二维数组需要写明参数int x[m][n]或int x[][n]

分配回收内存

C函数库中的malloc和free分别用于执行动态内存分配和释放。
这两个函数的原型如下所示，他们都在头文件stdlib.h中声明。

void *malloc ( size_t size );
void free ( void *pointer );
void *realloc (void ptr, size_t new_size );

malloc的作用是在内存的动态存储区中分配一个长度为size的连续空间。其参数是一个无符号整形数，返回值是一个指向所分配的连续存储域的起始地址的指针。必须注意的是，当函数未能成功分配存储空间（如内存不足）就会返回一个NULL指针。所以在调用该函数时应该检测返回值是否为NULL，确保非空之后再使用非常重要。malloc所分配的内存是一块连续的空间。同时，malloc实际分配的内存空间可能会比你请求的多一点，但是这个行为只是由编译器定义的。malloc不知道用户所请求的内存需要存储的数据类型，所以malloc返回一个void *的指针，它可以转换为其它任何类型的指针。

realloc函数用于修改一个原先已经分配的内存块的大小，可以使一块内存的扩大或缩小。当起始空间的地址为空，即ptr = NULL,则同malloc。
如果原先的内存尾部空间不足，或原先的内存块无法改变大小，realloc将重新分配另一块nuw_size大小的内存，并把原先那块内存的内容复制到新的内存块上。因此，使用realloc后就应该改用realloc返回的新指针。

二维数组分配空间

int[][] arr = new int[3][2];//初始化：定义一维数组，长度为3

arr[1] = new int[]{1,2,3,4};//初始化+赋值

string/char*篇

头文件先带上#include< string> #include< cstring>

函数	说明
str=str1+str2;str+=str3;	拼接
str.length()	求长度
str[i]	访问 string 字符串的元素
getline(cin, str); s=getline(s);	获取 string 输入
s.insert(pos,x);	在第pos个元素之后插入x
s.insert(pos,x,px,dx);	在第pos个元素之后插入x串从第px位起的dx个字符
s1.replace(起始位置，个数，替代字符)	s1.replace(0, 2, “A”);//把0下标及其后的共两个字符替换成A
int a=stoi(str1);	将字符串转换为整数
int a; string s=to_string(a);	将整数转换为字符串
reverse(s.begin(),s.end());	#include< algorithm>
sort(s.begin(),s.end());	将 s 串内部按字典序排序
s.count(x)	返回子串x在s中出现的次数
s.substr(pos,len)	返回 s 串中下标pos起截取长度为len的子串
erase(int x, int num)	从x位置向后删除(不包括x)，删除num个字符。
s.find(x)	查找子串x在s中第一次出现的首个位置，返回首字母下标；-1表示找不到子串
s.rfind(x)	查找字串x最后一次出现的位置
s1.index(字串，开始位置的下标，结束位置的下标)	检查某个子串是否包含在这个字符串中，如果在这个字符串中，返回第一次出现的下标，如果不在这个字符串中则报错.
Strcpy(des_str,ori_str)
Strcat(str1,str2)	小写转大写
Strcmp(str1,str2)//=0 >0 <0
strlen(s)	str实际长度，不包含’\0’
Strupr(str)	大写转小写
Strlwr(str)	小写转大写

串太长反斜杠\续行

查找函数之find()、rfind()、find_first_of()、find_first_not_of()、 find_last_of()、find_last_not_of()

n = s1.find('6');
n=s1.find('1', 1); //查找指定字符， 从某个位置向后开始查找， 返回该位置，若查找不到，则返回-1
int n = s1.find("23"); //查找字符串,若查找到返回字符串的起始位置(注意是起始位置),若查找不到，则返回-1
//注意：只有find和rfind函数可以查找字符串！其他函数查找会出现值不准确的情况！
//rfind()函数从后往前查找指定的字符或字符串
//find_first_of()函数查找第一个等于x字符的位置。
//find_first_not_of()函数查找第一个不等于x字符的位置。
//find_last_of()函数查找最后一个等于x字符的位置(注意是查找最后一个，而不是从后往前查找)。
//find_last_not_of()函数查找最后一个不等于x字符的位置。 用法同上

int substring(string &substr,string str,int pos,int len){
	//返回从pos开始len长度的子串
	if(pos<0||pos>=str.length||len<0||len>str.length-pos)
		return 0;
	if(substr.ch){
		free(substr.ch);
		substr.ch)=NULL;
	}
	if(len==0){
		substr.ch=NULL;
		substr.length=0;
		return 1;
	}else{
		substr.ch=(char*)malloc(sizeof(char)*(len+1));//多个'\0'
		int i=pos;
		int j=0;
		while(i<pos+len){
			substr.ch[j]=substr.ch[i];
			++i;++j;
		}
		substr.ch[j]='\0';
		substr.length=len;
		return 1;
	}
}

int index(string s,string t,int pos){
//主串第pos个字符后是否存在与t相等的子串，返回第一个子串的位置，否则返回0
	if(pos>0){
		n=strlen(s);m=strlen(t);i=pos;
		while(i<=n-m+1){
			substring(sub,s,i,m);
			if(strcompare(sub,t)!=0)i++;
			else return i;
		}
	}
	return 0;
}
int index(string s,string t,int pos){
//主串第pos个字符后是否存在与t相等的子串，返回第一个子串的位置，否则返回0
	i=pos;j=1;
	while(i<=strlen(s)&&j<=strlen(t)){
		if(s[i]==t[j]){++i;++j;}
		else {i=i-j+2;j=1;}
	}
	if(j>strlen(t))return i-strlen(t);
	else return 0;
}

字典序
先按照第一个字母、以 a、b、c……z 的顺序排列；如果第一个字母一样，那么比较第二个、第三个乃至后面的字母。如果比到最后两个单词不一样长（比如，sigh 和 sight），那么把短者排在前。

int strcompare(string s1,string s2){//先比字母，字母相同比长度
	for(int i=0,j=0;i<s1.length()&&j<s2.length();i++,j++){
		if(s1.ch[i]!=s2.ch[i])
			return s1.ch[i]-s2.ch[i];
		return s1.length-s2.length;
	}
}

易错tips

定义char a[ ][ ]时用scanf(“%s”,a[i]);输入每一行时最后都会加入一个换行符进去所以要多留一个空否则会出现很奇怪的错
注意向char数组和int数组放入数字再取出来是不一样的char数组取出来转变成int还需要减去’0’

串的置换算法

编写一个实现串的置换操作Replace(&S,T,V)的算法。对一个字符串S，使用一个长度小于S的串T替换S的子串V，并将替换后的串输出。

Status StrReplace(HString &S, HString T, HString V)//将v替换主串s中出现的所有与T相等的不重叠子串
{
	HString head, tail, temp, S0;
	int i, n;
	for (n = 0, i = 1; i <= (S.length - T.length + 1); i++)
	{
		SubString(temp, S, i, T.length);//用temp返回串s的第i个字符起长度为len的子串
		if (!StrCompare(temp, T))//返回0也就是相等时
		{
			SubString(head, S, 1, i - 1);
			int m = S.length - i - T.length + 1;
			SubString(tail, S, i + T.length, m);
			Concat(S0, head, V);//s0返回head+v
			Concat(S, S0, tail);
			i += V.length - 1;
			n++;
		}
	}
	printf("%s\n", S.ch);
	return n;
}

kmp算法

目的：有一个文本串S，和一个模式串P，实现主串和子串快速匹配，最终查找到P在S中的位置。解决暴力匹配过程中的回溯浪费，即主串和子串发生不匹配时子串仅后移一位继续匹配完全不相同的一段浪费。
基本元素
（1）next数组：为了编程方便，间接表示PMT（部分匹配值），它的值就是将PMT数组向后偏移一位得到的。next第0位的值，我们将其设成了-1，这只是为了编程的方便，并没有其他的意义。
求next数组的过程完全可以看成字符串匹配的过程，即以模式字符串为主字符串，以模式字符串的前缀为目标字符串，一旦字符串匹配成功，那么当前的next值就是匹配成功的字符串的长度。也就是说：从模式字符串的第一位(注意，不包括第0位)开始对自身进行匹配运算在任一位置，能匹配的最长长度就是当前位置的next值。
（2）匹配步骤
默认两个指针都从头开始匹配，两个指针指的值一样时都向后匹配下一个字符
如果刚开始就都不相同将整个子串向后挪一位；发现不匹配时将j指针挪动到新的位置（往后挪几位取决于当前最后一个匹配字符的next值是几，移动的位数=已匹配数-next[当前最后一个匹配字符的下标]）
（3）实例：要在主字符串"ababababca"中查找模式字符串"abababca"

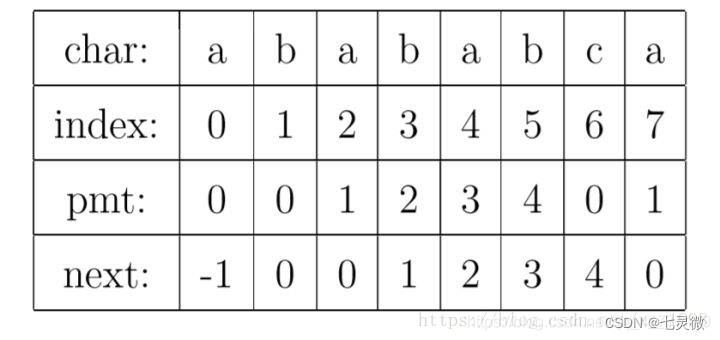
pmt的值易知，就是包括当前下标至串首的子串的前缀集合与后缀集合的交集中最长元素的长度。
next数组易知，是pmt数组往后移一个单位，前面补-1。定义为（不包括第0个字符，第0个字符默认next值为-1）不包括当前下标至串首的子串的前缀集合与后缀集合的交集中最长元素的长度。

next数组有两种一个是-1开始，一个是0开始，注意算法实现上的区分！之所以有这两种，是因为有些算法中串首下标是从0开始，故串首的next数组值对应-1；当串首下标从1开始时next数组对应0；

原理
（1）字符串的前缀和后缀
如果字符串A和B，存在A=BS，其中S是任意非空字符串，那就称B为A的前缀。例如，”Harry”的前缀包括{”H”, ”Ha”, ”Har”, ”Harr”}
我们把所有前缀组成的集合，称为字符串的前缀集合。后缀及后缀集合同理。
（2）PMT（部分匹配值）中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。
例如，对于”aba”，它的前缀集合为{”a”, ”ab”}，后缀集合为{”ba”, ”a”}。两个集合的交集为{”a”}，那么长度最长的元素就是字符串”a”了，长度为1，所以对于”aba”而言，它在PMT表中对应的值就是1。
对于字符串”ababa”，它的前缀集合为{”a”, ”ab”, ”aba”, ”abab”}，它的后缀集合为{”baba”, ”aba”, ”ba”, ”a”}，两个集合的交集为{”a”, ”aba”}，其中最长的元素为”aba”，长度为3。
如果在 j 处字符不匹配，主字符串在 i 位失配，也就意味着主字符串从 i−j 到 i 这一段是与模式字符串的 0 到 j 这一段是完全相同的。

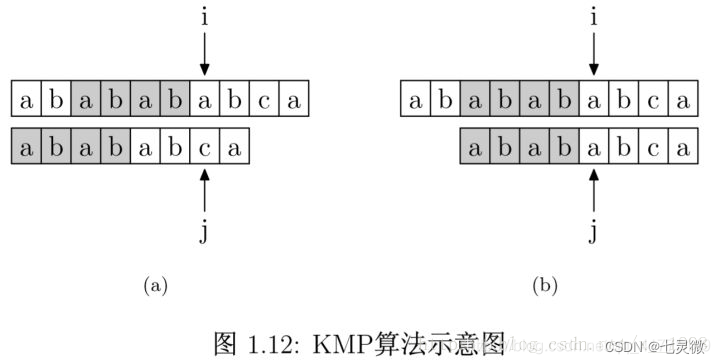
模式字符串从 0 到 j−1 ，在这个例子中就是”abababca”，其前缀集合与后缀集合的交集的最长元素为”abab”，长度为4。主字符串中i指针之前的 4 位一定与模式字符串的第0位至第 4 位是相同的，即长度为 4 的后缀与前缀相同。
我们就可以将这些已经匹配好的字符段的比较省略掉。做法是，保持i指针不动，然后将j指针指向模式字符串的PMT[j −1]位即可。
所以为了编程的方便，我们不直接使用PMT数组，（因为要j-1），而是将PMT数组向后偏移一位。我们把新得到的这个数组称为next数组。
匹配过程视频见 https://v.youku.com/v_show/id_XMzUyMjQyMTE3Mg==.html
（2：15）
代码

//串首下标为1且next数组以0开头的版本
void getnext(str substr,int next[]){
	int i=1,j=0;//j表示子串指针或者是next数组的值
	next[1]=0;//串首下标从1开始，当第一个不匹配时直接子串整体往右挪一位
	while(i<substr.len){
		if(j==0||substr.ch[i]==substr.ch[j]){
//当j=0时 j一定不表示子串指针，因为子串下标从1开始，
//那么代表next[j]=0即子串首跟下个主串字符对齐
			++i;++j;
			next[i]=j;
			//next[2]=1;无脑等于1，也就是说不匹配时直接将子串首与该位置对齐
		}else j=next[j];
	}
}
int kmp(str str,str substr,int next[]){
	int i=1,j=1;//串从数组下标1开始存储
	while(i<str.len&&j<substr.len){
		if(j==0||str.ch[i]==substr.ch[j]){
			++i;++j;
		}else j=next[j];
	}
	if(j>=substr.len) return j-substr.len;
	else return 0;//不匹配
}

求最大公共子串

动态规划(dynamic planning）思想
设置二维数组dp[][],dp[i][j]=k表示包括当前下标在内最长公共子串长度为k

string max_substring(string s1,string s2){
	string res="";
	int m=s1.length(),n=s2.length();
	int max=0,max_index=0;
	for(int i=0;i<m;i++){
		for(int j=0;j<n;j++){
			char c1=s1[i],c2=s2[j];
			if(c1==c2){
				if(j==0||j==0){
					dp[i][j]=1;
				}else dp[i][j]=dp[i-1][j-1]+1;
				if(dp[i][j]>max){
					max=dp[i][j];
					index=i;
				}
			}
		}
	}
	res=s1.substring(index-max+1,index);//第index-max+1下标起长度为index的串
	return res;
}

最简单的标记book

练习1 L1-011 A-B (20分)

本题要求你计算A−B。不过麻烦的是，A和B都是字符串 —— 即从字符串A中把字符串B所包含的字符全删掉，剩下的字符组成的就是字符串A−B。
输入格式：
输入在2行中先后给出字符串A和B。两字符串的长度都不超过10^4，并且保证每个字符串都是由可见的ASCII码和空白字符组成，最后以换行符结束。
输出格式：
在一行中打印出A−B的结果字符串。
输入样例：
I love GPLT! It’s a fun game!
aeiou
输出样例：
I lv GPLT! It’s fn gm!

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
int main()
{
	char a[10001];
	char b[10001];
	int c[128];
	int i;
	gets(a);
	gets(b);
	for(i=0;i<128;i++)
	{
	  c[i]=0;	
	}	
	for(i=0;i<strlen(b);i++)
	{
		c[(int)b[i]]=1;
	}
	for(i=0;i<strlen(a);i++)
	{
		if(c[(int)a[i]]==0)
		  printf("%c",a[i]);
	}
	printf("\n");
	return 0;
 }

最简单的hash表

练习：子串变位词

变位词：组成字母完全相同但顺序不一样，如abc acb。给定两个串a和b，问b是否是a的子串的变位词。例如输入a = hello, b = lel, lle, ello都是true,但是b = elo是false。

1.方法1：暴力
依次遍历b中字母检查是否在a里
2.方法2:先给两个串排序，然后比较
3.制作hash表
//制作a串的hash表
for (int i = 0; i < lena; ++i) 
	num[a[i] – ‘a’]++;////利用ascii码的差作为下标，形成对应的映射 如果出现0的情况则不是变位词
for (int j = 0; i < lenb; ++i) 
	if (num[b[i] – ‘a’] == 0)
		{	cout<<"false"<<endl;
			return 0;}
cout<<"true"<<endl;

排序

结构体的排序

调用sort函数，一定要加上这个头文件 #include< algorithm>
Sort函数有三个参数：
（1）第一个是要排序的数组的起始地址。
（2）第二个是结束的地址（最后一位要排序的地址）
（3）第三个参数是排序的方法，可以是从大到小也可是从小到大，还可以不写第三个参数，此时默认的排序方法是从小到大排序。
【注意】这里的第三个参数就是自己定义的比较方式的函数，比如下面的例子我定义的函数名字是cmp，（是bool类型），我这个函数返回的是 a>b,所以这里调用了sort之后数组里的元素按照从小到大的顺序排列

练习1 奖学金

[NOIP2007]奖学金
某小学打算为学习成绩优秀的前5名学生发奖学金。期末，每个学生都有3门课的成绩:语文、数学、英语。先按总分从高到低排序，如果两个同学总分相同，再按语文成绩从高到低排序，如果两个同学总分和语文成绩都相同，那么规定学号小的同学排在前面，这样，每个学生的排序是唯一确定的。
任务：先根据输入的3门课的成绩计算总分，然后按上述规则排序，最后按排名顺序输出前五名名学生的学号和总分。注意，在前5名同学中，每个人的奖学金都不相同，因此，你必须严格按上述规则排序。例如，在某个正确答案中，如果前两行的输出数据(每行输出两个数:学号、总分) 是:
7 279
5 279
这两行数据的含义是:总分最高的两个同学的学号依次是7号、5号。这两名同学的总分都是 279 (总分等于输入的语文、数学、英语三科成绩之和) ，但学号为7的学生语文成绩更高一些。如果你的前两名的输出数据是:
5 279
7 279
则按输出错误处理，不能得分。

#include<iostream>
#include<algorithm>
using namespace std;
struct student{
    int c;//语文分数
    int s;//数学分数
    int y;//英语分数
    int num;//学号
    int sum;//每个人的总分
}p[500];
bool cmp(const student&a,const student&b)
{
    if(a.sum!=b.sum)//如果总分不相同，就返回总分高的那一个
        return a.sum>b.sum;
    else if(a.sum==b.sum&&a.c!=b.c)//如果总分相同，就返回总分语文高的那一个
        return a.c>b.c;
    else if(a.sum==b.sum&&a.c==b.c&&a.num!=b.num)
//如果总分相同，语文分相同，就返回总分学号小的那一个
        return a.num<b.num;
}
int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n;i++)
        {
        	cin>>p[i].c>>p[i].s>>p[i].y;//输入信息                                           
        	p[i].num=i+1;//序号即学号
        	p[i].sum=p[i].c+p[i].s+p[i].y;//算出每个人的总分
		}
    sort(p,p+n,cmp);//排序
    for(int i=0;i<5;i++)//输出前五名的学号和总分
        cout<<p[i].num<<" "<<p[i].sum<<endl;
    return 0;
}

直接插入排序

void InsertSort(ElemType A[],int n)
{
	int i,j;
	for (i = 2;i <= n;i ++)
		if (A[i] < A[i-1]) {
			A[0] = A[i];
			for (j = i-1;A[0] < A[j]; --j)
				A[j+1] = A[j];
			A[j+1] = A[0];
		}
}

练习：前m个元素递增有序，后n个元素递增有序，设计算法使整个顺序表有序

顺序表a[]元素存储在数组下标1～m+n范围内。
算法思路：将数组[1,…m]视为一个已经过m趟插入排序的表，从第m+1趟开始将后n 个元素依次插入前面的有序表中

void insert(int a[],int m,int n){
	int i,j;
	for(i=m+1;i<=m+n;i++){
		a[0]=a[i];
		for(j=i-1;a[j]>a[0];j--)a[j+1]=a[j];
		a[j+1]=a[0];
	}
}

折半插入排序

void InsertSort(ElemType A[],int n)
{
	int i,j,low,high,mid;
	for (i = 2;i <= n;i ++){
		A[0] = A[i];
		low = 1;high = i - 1;
		while (low <= high) {
			mid = (low+high)/2;
			if (A[mid] > A[0]) high = mid-1;
			else low = mid+1;
		}
		for (j = i-1;j >= high+1;--j)
			A[j+1]=A[j];
		A[high+1] = A[0];
	}
}

冒泡排序

void BubbleSort(ElemType A[],int n)
{
	for (i = 0;i < n-1;i ++) {
		flag = false;
		for (j = n-1;j > i;j --)
			if (A[j-1] > A[j]) {
				swap(A[j-1],A[j]);	
			}
		if (flag == false)
			return;
	}
}

练习：双向冒泡排序

排序过程中交替改变扫描方向

void sort(int a[],int n){//数据存在下标0~n-1
	int left=0,right=n-1;
	int flag=0;
	while(flag==0){
		flag=1;
		int k=left;
		while(k<right){
			if(a[k]>a[k+1]){swap(a[k],a[k+1]);flag=0;}
			k++;
		}
		right--;
		k=right;
		while(k>=left){
			if(a[k-1]>a[k]){swap(a[k],a[k-1]);flag=0;}
			k--;
		}
		left++;
	}
}

快速排序

基于二分法的思想。

void QuickSort(ElemType A[],int low,int high)
{
	if (low < high) {
		int pivotpos = Partition(A,low,high);
		QucikSort(A,low,pivotpos-1);
		QucikSort(A,pivotpos+1,high);
	}
}

int Partition(ElemType A[],int low,int high)
{
	ElemType pivot = A[low];
	while (low < high) {
		while (low < high&&A[high]>=pivot) high --;
		A[low] = A[high];
		while (low < high&&A[low] <= pivot) ++low;
		A[high] = A[low];
	}
	A[low] = pivot;
	return low;
}

练习：快速排序非递归算法

练习：0-1交换

把一个0-1串（只包含0和1的串）进行排序，你可以交换任意两个位置，问最少交换的次数？
分析：快排partition：最左边的那些0和最右边的那些1都可以不管；从左开始扫到第一个出现1的位置，从右扫第一个出现0的位置然后进行交换即可。

int answer = 0;	//次数
for (int i = 0, j = len – 1; i < j; ++i, --j) {
	for (;(i < j) && (a[i] == ‘0’);++i);
	for (;(j > i) && (a[j] == ‘1’); --j);
	if (i <j) ++answer;
}

练习2：交换星号

一个字符串只包含和数字，请把它的星号都放开头。

//这个方法会打乱数字顺序
for (int i = 0, j = 0; j < n; ++j) 
		if (s[j] == ‘＊’） swap(s[i++], s[j]);
//不打乱数字顺序的方法 直接倒着覆盖 省空间
int j = n - 1;
	for (int i = n - 1; i >= 0; --i) 
			if (isdigit(s[i])) s[j--] = s[i];//isdigit是否是数字
	for (; j >= 0; --j) s[j] = ‘*’;

练习：输出前m大的数

排序后再输出，复杂度O(nlogn）
用分治处理：复杂度 o(n+m1ogm)
思路：把前m大的都弄到数组最右边，然后对这最右边m个元素排序，再输出
关键：0(n）时间内实现把前m大的都弄到数组最右边
T (n) = T (n/2) + an
= T (n/4) + an/2 + an
= T (n/8) + an/4 + an/2 + an
…
=T(1）+…+ an/8 + an/4 + an/2 + an
< 2an
即o(n）

练习：奇数在前偶数在后

利用快速排序实现顺序表中奇数在前偶数在后。

//有两种快速排序实现方法，交换法或者是挖坑法
void move(int a[],int len){
	int i=0,j=len-1;
	while(i<j){
		while(i<j&&a[i]%2!=0)i++;
		while(i<j&&a[i]%2==0)j--;
		if(i<j)swap(a[i],a[j]);
		i++;j--;
	}
}

练习：枢轴值随机选的快速排序划分算法

枢轴值是随机从当前子表中选择的。

int partition_random(int a[],int low,int high){
	int rand_index=low+rand()%(high-low+1);
	swap(a[rand_index],a[low]);
	int pivot=a[low];
	while(low<high){
		while(low<high&&a[high]>=pivot)high--;
		a[low]=a[high];
		while(low<high&&a[low]<=pivot)low++;
		a[high]=a[low];
	}
	a[low]=pivot;
	return low-1;
}

练习：找出数组中第k小的元素 a[1…n]升序

可以利用小顶堆；也可以排序后直接取用；还有一种新方法，利用快速排序划分操作，划分后a[m]=pivot；若m==k，则pivot即所求元素；m<k，则所求元素在a[m+1,n]中，在这区间递归下去查找第k-m小的元素。m>k，则所求元素在a[1,m-1]中，在这区间递归下去查找第k小的元素。

int kth(int a[],int low,int high,int k){
	int pivot=a[low];
	int low_temp=low,high_temp=high;
	while(low<high){
		while(low<high&&a[high]>=pivot)high--;
		a[low]=a[high];
		while(low<high&&a[low]<=pivot)low++;
		a[high]=a[low];
	}
	a[low]=pivot;
	if(low==k)return a[low];
	else if(low>k)return kth_elem(a,low_temp,low-1,k);
	else return kth_elem(a,low+1,high_temp,k);
}

练习：两个不相交子集满足|n1-n2|最小，|s1-s2|最大

由n个正整数构成的集合a[]，将其划分成两个不相交子集a1,a2，元素个数分别为n1,n2，元素之和分别为s1,s2，设计算法满足满足|n1-n2|最小，|s1-s2|最大
算法思想：若I=floor(n/2)则分组完成；若i<floor(n/2)，则继续对i之后的元素进行划分；若i>floor(n/2)，则对于i之前的元素进行划分。

int setpartition(int a[],int n){
	int pivot,low=0,high=n-1,flag=1,k=n/2,i;
	while(flag){
		pivot=a[low];
		while(low<high){
			while(low<high&&a[high]>=pivot)high--;
			a[low]=a[high];
			while(low<high&&a[low]<=pivot)low++;
			a[high]=a[low];
		}
		a[low]=pivot;
		if(low==k)return flag=0;
		else if(low>k)high--;
		else low++;
	}
}

练习：荷兰国旗问题

给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。
我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
必须在不使用库内置的 sort 函数的情况下解决这个问题。
示例 1：
输入：nums = [2,0,2,1,1,0]
输出：[0,0,1,1,2,2]
示例 2：
输入：nums = [2,0,1]
输出：[0,1,2]

思想：0的部分用low指针，1的部分用mid指针，2的部分用high指针，注意交换的时候有可能将1换到0的部分等，指针什么时候移动很重要。

#include <cstdlib>
#include <iostream>
#include <algorithm>
using namespace std;

char a[50];

void Flag_Arrange(char a[], int n)
{
    int i = 0, j = 0, k = n - 1;
    while (j <= k) {
        switch (a[j]) {
            case 'R': swap(a[i], a[j]); i++; j++; break;
            case 'W': j++; break;
            case 'B': swap(a[j], a[k]); k--;
        }
    }
}

int main()
{
    cin >> a;
    int n = strlen(a);
    Flag_Arrange(a, n);
    for (int i = 0; i < n; i++) cout << a[i];
    return 0;
}

选择排序

void Selectsort(ElemType A[],int n)
{
	for (i = 0;i < n-1;i ++) {
		min = i;
		for (j = i+1;j < n;j ++)
			if (A[j] < A[min]) min = j;
		if (min != i) Swap(A[[i],A[min]);
	}
}

归并排序

/*merge功能是将前后相邻两个有序表归并成一个有序表 
a[low...mid]与a[mid+1...high]
需要同样长的一个辅助数组*/
int *b=(int *)malloc((n+1)*sizeof(int));
void merge(int a[],int low,int mid,int high){
	for(int k=low;k<=high;k++)b[k]=a[k];//a数组复制到b数组
	for(i=low,j=mid+1,k=i;i<=mid&&j<=high;k++){
		if(b[i]<=b[j])a[k]=b[i++];
		else a[k]=b[j++];
	}
	while(i<=mid)a[k++]=b[i++];
	while(j<=high)a[k++]=b[j++];
}

void MergeSort(ElemType A[],int low,int high)
{
	if (low < high) {
		int mid = (low + high)/2;
		MergeSort(A,low,mid);
		MergeSort(A,mid+1,high);
		Merge(A,low,mid,high);
	}
}

归并两个升序链表

void Merge(LNode *L1, *L2){            //数组A、B长度分别为n、m
   LNode *p=L1->next, *q=L2->next;    //p、q指向L1、L2第一个元素
   LNode *r=L1;                      //新链表头节点为L1，r指向末尾
   LNode *pn, *qn;                    //用来暂存p->next和q->next
   while (p!=null && q!=null)         //直到有一个链表遍历完
      if (p->data<q->data){            //将小的那个数存入新链
          pn=p->next;                    //pn为p下一个元素
          r->next=p;                    //p插入到r后面
          p->next=null;                //这是新链最后一个元素
          r=p;                           //尾指针r指向最后一个元素
          p=pn;                          //p指向p下一个元素
      }
      else{ 
          qn=q->next;                  //qn为q下一个元素
          r->next=q;                   //q插入到r后面
          q->next=null;               //这是新链最后一个元素
          r=q;                          //尾指针r指向最后一个元素
          q=qn;                         //q指向q下一个元素
      }
   if (p!=null)
      r->next=p;                      //将剩余部分连到r后面
   if (q!=null)
      r->next=q;                      //将剩余部分连到r后面
   /*L1是合并后的升序链表，注意此时r已经不是指向尾元素的指针了*/
}

希尔排序

void shell_sort(int a[],int n){
	int d,i,j;
	for(d=n/2;d>=1;d=d/2)
		for(i=d+1;i<=n;i++)
			if(a[i]<a[i-d]){
				a[0]=a[i];
				for(j=i-d;j>0&&a[0]<a[j];j-=d)
					a[j+d]=a[j];
				a[j+d]=a[0];
			}
}

最简单的桶排序/计数排序版本1

利用数组序号的自顺序进行排序输入输出

int book[1001],i,j,t,n;//size=num-1
for(i=0;i<=1000;i++)
	book[i]=0;
scanf("%d",&n);
for(i=1;i<=n;i++)
{
	scanf("%d",&t);
	book[t]++;
}
for(i=1000;i>=0;i--)
	for(j=1;j<book[i];j++)//book[i]里有几就打印几次
		printf("%d",i);

计数排序版本2

将排序结构放到另一个表中，扫描一趟待排序表，统计有c个记录关键码比该记录的关键码小，则在新表c位置放入该记录。

void countsort(int a[],int b[],int n){
	int cnt;
	for(i=0;i<n;i++){
		for(j=0,cnt=0;j<n;j++)
			if(a[j].key<a[i].key)cnt++;
		b[cnt]=a[i];
	}
}

堆排序

大顶堆：所有父节点都比子节点大。
小顶堆：所有父节点都比子节点小。
如何建立堆？
1. 往堆中一次插入元素，插入第i个元素时间复杂度是o(logi),插入所有元素时间复杂度是o(nlogn)，因为要调整符合大小特性。
2. 还有更快(常用)的方法是先插入，从最后一个非叶子结点（编号n/2）开始依次调整。这种方法复杂度是o(n)
向上调整：如果加进来的数插入末尾后不符合堆的大小特性，则需要向上调整。时间复杂度logn
向下调整
堆排序：每次取顶部元素将其输出或放入新数组，直到堆为空为止。时间复杂度o(nlogn)
应用：求第k大的数/第k小的数
应用：长度为n的数组使每个值排序后位置前后差距不超过k(k<=n)
堆排序尽可能位置少移动，因为只做向上/向下调整，移动了[i-i/2]或者[2i-i]个位置

//wangdao版本
void BuildMaxHeap(Elemtype A[],int len) 
{
	for (int i = len/2;i > 0;i --)
		HeadAdjust(A,i,len);
}

void HeadAdjust(ElemType A[],int k,int len)//大顶堆的向下调整
{
	A[0] = A[k];
	for (i = 2*k;i <= len;i *= 2) {
		if (i < len&&A[i] < A[i+1])
			i ++;
		if (A[0] >= A[i]) break;
		else {
			A[k] = A[i];
			k = i;
		}
	} 
	A[k] = A[0];
}

void HeapSort(ElemType A[],int len)
{
	BuildMaxHeap(A,len);
	for (i = len;i > 1;i --) {
		Swap(A[i],A[1]);
		HeadAdjust(A,1,i-1);	
	}
}


//小顶堆
//建立堆1
n=0;
for(i=1;i<=m;i++)
{
	n++;
	cin>>&h[n];
	siftup(n);
}
//建立堆（常用）
void create(){
	int i;
	for(i=n/2;i>=1;i--)
		siftdown(i);
	return;
}
//堆排序其中一步：删除大顶堆的顶部元素
int deletemax(){
	int t=h[1];
	h[1]=h[n];
	n--;
	siftdown(1);//向下调整
	return t;//返回max
}
//向上调整
void siftup(int i)//传入一个需要调整的节点编号
{
	int flag=0;//标记是否调整
	if(i==1)return;//已经在堆顶无需调整
	while(i!=1&&flag==0){
		if(h[i]<h[i/2])
			swap(i,i/2);
		else flag=1;
		i/=2;//更新节点，便于继续向上调整
	}
	return;
}
//向下调整
void siftdown(int i)//传入一个需要调整的节点编号，输入1即从堆的顶点向下调整
{
	int t,flag=0;//标记是否向下调整
	while(i*2<=n&&flag==0){
		if(h[i]>h[i*2])//父比子大
			t=i*2;//t记录值最小的节点编号
		else t=i;
		if(i*2+1<=n)//如果有右孩子
		{
			if(h[t]>h[i*2+1])//父比子大
			t=i*2+1;//t记录值最小的节点编号
		}
		if(t!=i){
			swap(t,i);
			i=t;//更新编号为刚才与它交换的儿子节点，便于继续向下调整
		}else flag=1;//无需调整
	}
	return;
}

最简单的去重

//假设经过排序之后
for(i=2;i<=n;i++)
	if(a[i]!=a[i-1])
		printf("%d",a[i]);

主元素问题

一个序列中已知一个数出现次数超过一半，求这个数。
特性：在原序列中去除两个不一样的数，那么在原序列中出现次数超过一半，则在新序列中出现次数也必然超过一半。
在这里插入图片描述

线性表篇

线性表是具有相同特性的数据元素的一个有限序列，其中数据元素的个数n定义为表的长度，当n = 0时称为空表；在非空的线性表，有且仅有一个开始结点,其没有直接前驱，仅有一个直接后继；有且仅有一个终端结点,其没有直接后继，仅有一个直接前驱；其余的内部结点都仅有一个直接前驱和一个直接后继。
在这里插入图片描述

新建一个节点可用 
node *p=new node();

struct的链表里也可以用构造函数
node(int _val):val(_val),next(NULL){}

指针调用 p->next p->val
节点 p.next p.val

auto p=new node(1);//auto 自识别类型 1指的是利用构造函数赋值

最简单的逆置

void reverse(int R[],int l,int r){
	int i,j,temp;
	for(i=1,j=r;i<j;++i,--j){
		temp=R[i];
		R[i]=R[j];
		R[j]=temp;
	}
}

练习1:将一维数组中的序列循环左移p个位置

{x0,…xn-1}变换到{xp,xp+1,…,xn-1,x0,x1,…xp-1}
思路很明显，首先整体逆置得到{xn-1…x0}，再将前p个逆置，后p个逆置。

头节点的作用

对在第一个结点（储存第一个数据）之前插入时，代码可以与在中间插入时做到代码统一，若没有头结点，在第一个结点前插入时，要特别写一段代码。如果有头结点，头结点的next域实时指向第一个结点，这样的话头指针就可以不用再更新。
使得空表与非空表实现代码统一，若没有头结点并且为空表时，头指针为NULL，但如果有头结点时，不论是不是空表，头指针始终不为NULL。
总之，头结点出现，可以实现代码的统一。

线性链表

练习:快慢指针的应用

删除链表倒数第n个节点
i指针先走1格，之后每次都等于走完n个格的i指针，然后继续让j指针走。
j指针一次走n格，假如下一个节点为空则删除i指针后面的元素即可。
求链表最中间的节点
一个指针先走1格
另一个指针一次走2格

练习:生成26个字母的线性表，并实现对特定字母的插入和删除的程序

#include <stdio.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
#define YES 1
#define NO 0
#define OK 1
#define ERROR 0
#define SUCCESS 1
#define UNSUCCESS 0
#define OVERFLOW -2
#define UNDERFLOW -3
#define LIST_INIT_SIZE 100
#define LISTINCREMENT 10
typedef int Status;
typedef char ElemType;
typedef struct {
    ElemType *elem;
    int length;
    int listsize;
}SqList;

Status InitList(SqList *L){
    (*L).elem =(ElemType *)malloc(LIST_INIT_SIZE *sizeof(ElemType));
    if(!(*L).elem) exit(OVERFLOW);//分配失败
    (*L).length=0;
    (*L).listsize = LIST_INIT_SIZE;
    return OK;
}

Status ListInsert(SqList *L,int i,ElemType e)//插入第i位即下标i-1 值为e
{   ElemType *newbase;
    ElemType *p,*q;
    if(i<1||i>(*L).length+1)return ERROR;
    if((*L).length>=(*L).listsize){
        newbase = (ElemType *) realloc ((*L).elem,((*L).listsize+LISTINCREMENT)*sizeof(ElemType));
        if(!newbase) exit (OVERFLOW);
        (*L).elem =newbase;
        (*L).listsize +=LISTINCREMENT;

    }
    q=&((*L).elem[i-1]);
    for(p=&((*L).elem[(*L).length-1]);p>=q;--p)
        *(p+1) = *p;
    *q=e;
    ++(*L).length;
    return OK;

}

Status ListDelete(SqList *L,int i,ElemType *e)
{
    int j;
    ElemType *p,*q;
    if(i<1||i>(*L).length)return ERROR;
    p=&(*L).elem[i-1];
    *e=*p;
    q=(*L).elem+(*L).length-1;//指向最后的一个节点
    for(;p<=q;++p)
        *(p-1)=*p;
    (*L).length--;
    return OK;
}
Status GetElem(SqList L,int i ,ElemType *e )
{
    if(i<1||i>L.length)return ERROR;
    else *e=L.elem[i-1];
    return OK;
}

int main(){
SqList L;
int i;
ElemType e,z;
InitList (&L);
for(int i=1; i<=26;i++)
    ListInsert(&L,i,(char)i+64);

ListDelete(&L,4,&z);
GetElem(L,4,&z);
printf("%c\n",z);

ListInsert(&L,4,'D');
GetElem(L,4,&z);
printf("%c\n",z);
}

练习2:约瑟夫环

约瑟夫环问题是一个很经典的问题：一个圈共有N个人（N为不确定的数字），第一个人的编号为1，假设这边我将第一个人的编号设置为1号，那么第二个人的编号就为2号，第三个人的编号就为3号，第N个人的编号就为N号，现在提供一个数字M，第一个人开始从1报数，第二个人报的数就是2，依次类推，报到M这个数字的人出局，紧接着从出局的这个人的下一个人重新开始从1报数，和上面过程类似，报到M的人出局，直到N个人全部出局，请问，这个出局的顺序是什么？

方法1:数组方式
数组：一开始将所有的元素初始化为0，代表一开始所有人都处于未出局的状态，一旦某个人出局，将其对应的数组元素的值设为非0的一个数，代表他不再报数。
i：既代表数组的下标，也代表每个人的编号
k：用来计数，从0开始，一旦k的值达到M，代表当前这个人需要出局，并且k的值需要重新置为0，这样才能找到所有需要出局的人

方式2:实现循环链表

//方法1
#include<bits/stdc++.h>
using namespace std;
//用数组实现约瑟夫环问题
int a[110]={0};   //元素值为0表示未出局 
//i既代表数组的下标，也代表每个人的编号
//k是用来计数的，一旦k的值达到m，代表此人需要出局，并且k需要重新计数，这样才能够找出所有需要出局的人
//数组的0代表未出局的人，数组非0代表出局的人，未出局的人需要报数，出局的人不需要报数 
int main()
{
	int N,M;
	int cnt=0,i=0,k=0;  //cnt表示目前出局的人数 
	cin>>N>>M;  //表示总共有n人，数到数字m时出局 
	while(cnt!=N) //因为要求N个人的出局顺序，因此当cnt（用来统计已经出局的人）未达到n时，需要循环不断报数 
	{
		i++;   //i是每个人的编号 
		if(i>N) i=1;  //这里需要特别注意：i的值是不断累加的，一旦发现i的值>N，那么i需要重新从第1个人开始
		              //数组要从第一个元素重新开始一个一个往后判断 
		if(a[i]==0)   //只有元素值为0的人 才需要报数，元素值为非0的代表已经出局了，不用报数 
		{
			k++;
			if(k==M)     //代表已经某个人已经报了M这个数，需要出局 
			{
				a[i]=1;  //编号为i的这个人出局 
				cnt++;   //出局的人数+1 
				cout<<i<<" ";  //输出出局的人的编号 
				k=0;   //清空k，让下一个人重新从1开始报数   
			}
		}
	}
	return 0;
} 

//方法2
typedef struct node  //typedef用来重命名struct node这种数据类型，将其命名为Node 
{
	int data;
	struct node* next;
}Node;

	//初始化循环链表
	Node *head = NULL,*p=NULL,*r=NULL;   //head为头指针，指向链表的第一个结点，一开始赋值为NULL,代表不指向任何结点 
	head = (Node*)malloc(sizeof(Node));  //让head指向一个实际的空间
	if(NULL==head)  //内存空间可能会申请失败,大多数情况不会申请失败 
	{
			cout<<"Memory Failed!";
			return;
	} 
	head->data=1;       //从1开始编号 
	head->next=NULL;    //一开始整个链表只有一个Node(结点)，这个Node有两个域，分别是data和next
	                    //data从1开始，next指向NULL，总共需要N个结点，现在创建了一个，还需要N-1个 
    p=head;             //head要保持不能改变，才能够找到链表的起始位置，一开始p也指向第一个结点
	                    //p等一下会被使用，用它可以便于创建剩下的N-1个结点 
	
	//尾插法创建链表,已经有一个1号结点了，还需要创建剩下的n-1个结点 
	for(int i=2;i<=N;i++)
	{
		r=(Node*)malloc(sizeof(Node)); 
		r->data=i;
		r->next=NULL;
		//插入结点 
		p->next=r;
		p=r;
	}
	//创建循环链表
	p->next=head;   //最后一个结点的next指向头结点
	p=head;         //为后续方便，将p指向头结点
	
	//开始游戏
	while(p->next!= p)  //如果p的next=p，说明目前只有一个元素 
	{
		for(int i=1;i<M;i++)  //报到数字为M的时候出局 
		{
			  r=p;   //保留出局的前一个结点 
			  p=p->next; //p指向的是要出局的这个结点，需要保留前一个结点
		}
		// 输出
		cout<<p->data<<" ";
		r->next=p->next;    //删除p的目的，此时p指向哪里？  ：
		free(p);  
		p=r->next;  //更新p重新进行报数 
	} 
	cout<<p->data;

练习3:Joseph问题

练习2的变形。
约瑟夫(Joseph)问题的一种描述是：编号为 1，2，…,n 的 n 个人按顺时针方向围坐一圈，每人持有一个密码（正整数），一开始任选一个整数作为报数上限 m,从第一人开始按顺时针方向从自 1 开始顺序报数，报到 m 时停止报数。报 m 的人出列，将他的密码作为新的 m 值，从他的顺时针方向上的下一个人开始重新从 1 报数，如此下去，直至所有人全部出列为止，设计一个程序求出出列顺序。
采用单向循环链表模拟此过程，按照出列的顺序印出各人的编号

/**
	Joseph问题
	Author：BaoMinyang
	Date：2018/09/20 
*/
#include<stdio.h>
#include<stdlib.h>
#include<iostream>
using namespace std;

#define LIST_INIT_SIZE 100
#define LISTINCREMENT 10
#define OK 1
#define ERROR 0
#define OVERFLOW -2

typedef int ElemType;
typedef int DeleteType;
typedef int Status;

//定义链表结点 
typedef struct LNode{
	ElemType num;
	ElemType data;
	LNode *next;
}*LinkList;

//定义被删除的结点编号变量 
DeleteType del_num;

//链表初始化 
Status InitRList(LinkList &L){
	L = (LinkList) malloc (sizeof(LNode));
	if(!L) exit(OVERFLOW);
	L->next = NULL;
	return OK;
}

//创建链表 
Status CreateRList(LinkList &L,int a[],int n){
	LinkList r = L;
	for (int i = 0; i < n; ++i){
		LinkList q = (LinkList) malloc (sizeof(LNode));
		q->num = i+1;
		q->data = a[i];
		r->next = q;
		r = q;
		printf("num:%d,p:%d\n",q->num,q->data);
	}
	r->next = L->next; 
	return OK;
}

//删除链表结点 
LinkList DeleteRList(LinkList &m,int key){
	LinkList p,q;
	p = m;
	for (int j = 0; j < key-1; j++) p = p->next;
	q = p->next;
	p->next = q->next;
	printf("num:%d出列\n",q->num);
	del_num = q->data;
	free(q);
	return p;
}

//游戏开始 
Status Joseph(LinkList &L,int n,int key){
	LinkList q = L;
	bool isDone = 1;
	while (n-1){
		if (isDone){
			q = DeleteRList(q,key);
			isDone = 0;
		}
		else {
			q = DeleteRList(q,del_num);
		}
		n--;
	}
	return q->num;
}

int main(){	

	int a[35],n=0,init_m;
	LinkList L;
	
	printf("请输入m的初始值:");
	scanf("%d",&init_m);
	
	printf("请输入参加游戏的人数n:");
	scanf("%d",&n);
	
	printf("请输入每个人的密码:");
	for (int i = 0; i < n; ++i){
		scanf("%d",&a[i]);
	}
	
	InitRList(L);
	
	CreateRList(L,a,n);
	
	printf("游戏开始:\n"); 
	printf("最终剩下的是num:%d",Joseph(L,n,init_m));
	
	return 0;
}

练习：逆置循环双链表

思想：只交换节点中的data，前后指针不变。

void reverse(){
	linklist *begin=_head;
	linklist *end=_tail;
	if(begin==end)//节点数为0，直接免于交换
		return;
	while(begin!=end && begin->next!=end)//节点数剩1的时候也免于交换
	{
		swap(begin->data,end->data);
		begin=begin->next;
		end=end->prior;
	}
}

练习：找到两个单链表第一个公共节点

第一种思路：p q指针每次一次往后，当走到链表末尾即null时再换到另一个开头继续往后走，最终两者相遇的地方就是第一次交汇的地方
原理图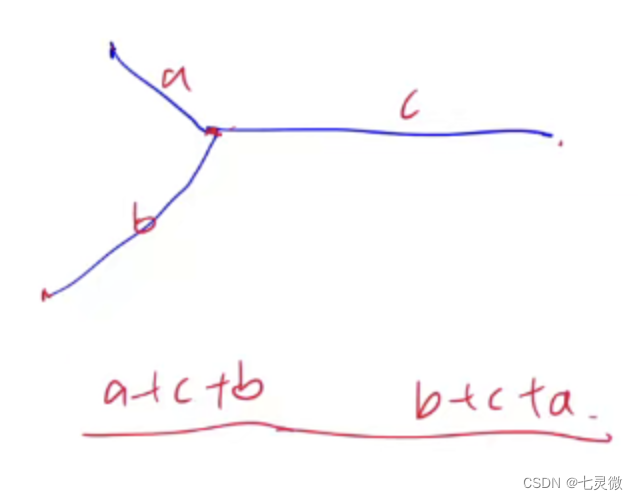在这里插入图片描述
当然另一种情况就是本来就没有交汇：而这一种情况依然可以沿用之前的思路，最终同样两者都会等于null

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode *p1 = headA;
        ListNode *p2 = headB;

        while (p1 != p2) {
            if(p1 != NULL)//p1没有走到结尾
                p1 = p1->next;//p1指向下一个节点
            else//p1走到结尾
                p1 = headB;//p1指向另一个链表头
            if(p2 != NULL)//p2没有走到结尾
                p2 = p2->next;//p2指向下一个节点
            else  //p2走到结尾 
                p2 = headA;//p2指向另一个链表头
        }
        return p1;
    }
};

第二种思路：两个链表结构类似Y形，暴力很简单，在此基础上优化的思路为，两个链表由于长度不一定相等，则不一定能同时走到第一个公共节点，故先算出两个链表的长度，让比另一个长k个节点的链表在一开始先多走k个，再两个链表一起走。时间复杂度由o(len1*len2)->o(len1+len2)

linklist search_1common(linklist l1,linklist l2){
	int len1=length(l1),len2=length(l2);
	linklist longlist,shortlist;
	if(len1>len2){
		longlist=l1->next;
		shortlist=l2->next;
		dist=len1-len2;
	}else{
		longlist=l2->next;
		shortlist=l1->next;
		dist=len2-len1;
	}
	while(longlist!=shortlist&&!longlist&&!shortlist){
		longlist=longlist->next;
		shortlist=shortlist->next;
	}
	if(!lontlist)return longlist;
	else return NULL;
}

练习：判断循环双链表是否对称

思路：p从左向右扫描，q从右向左扫描，直到他们指向同一个节点（节点个数为奇数）或者相邻（节点个数为偶数）为止。若他们所指节点值相同则继续执行，否则返回0，若全部比较完则返回1.

int symmetry(dlinklist l){
	dnode *p=l->next,*q=l->prior;
	while(p!=q&&q->next!=p){
		if(p>data==q->data){
			p=p->next;
			q=q->prior;
		}else return 0;
	}
	return 1;
}

栈

判断是否是正确的出栈序列

整数1～n从小到大依次进栈，期间可出栈，判断序列是否是正确的出栈序列。
原理：
m出栈后x出栈，
若m<x，则m+1~x-1元素还在栈中，接下来出栈要么大于x，要么肯定是x-1,x-2…m+1顺序出栈；若m与x相邻则x=m+1是连续出栈，暂时符合要求，当m>1时此时栈里可能是连续的小于x的数，也可能是小于x的数不连续的从栈顶到栈底降序排列；
若x<m，则x+1~m-1肯定早就出栈了，不确定是否正确，当x>1时栈里可能是连续的小于x的数，也可能是小于x的数不连续的从栈顶到栈底降序排列，这个时候就要实际模拟出栈剩余序列看下是否相符。

bool judge(int a[],int n){
	int i,j,m=0;//m记录之前出栈的最大值
	stack<int> s;
	for(i=0;i<n;i++){
		if(a[i]>m+1){
			for(j=m+1;j<a[j];j++)
				s.push(j);
			m=a[i]
		}
		if(a[i]==m+1)
			m=a[i];
		if(a[i]<m){
			if(a[i]==s.top())
				s.pop();
			else return false;
		}
	}
	return true;
}

数制转换

//简单版
void f(int n) //递归
{	if(n==0) return;  
	f( n/2 );  
	cout<<(n%2); }
void f（）//非递归，栈
{	InitStack(S);
	scanf("%d",N);
	while(N)
	{	Push(S,N%2)； 
		N=N/2；
	}
    while( !StackEmpty(S) )
    {   Pop(S,e);
       	printf("%d",e);
    }
}
//源程序版
#include<stdio.h>
#include<stdlib.h>
#include<iostream>
using namespace std;

#define STACK_INIT_SIZE 100
#define STACKINCREMENT 10
#define OK 1
#define TRUE 1
#define FALSE 0
#define ERROR 0
#define OVERFLOW -1
#define MAXSIZE 100
typedef int Status;
typedef int SElemType;

typedef struct {
    SElemType *base;
    SElemType *top;
    int stacksize;}SqStack;
    
Status InitStack(SqStack &s){
	s.base = (SElemType *)malloc(STACK_INIT_SIZE *sizeof(SElemType));
	if(!s.base)exit(OVERFLOW);
	s.top=s.base;
	s.stacksize=STACK_INIT_SIZE;
	return OK;
}

Status Push(SqStack &s,SElemType e)//插入新元素e
{
    if(s.top-s.base>=s.stacksize){//栈满 需要追加存储空间
        s.base=(SElemType *)realloc(s.base,(s.stacksize +STACKINCREMENT)* sizeof(SElemType));
        if(!s.base)exit(OVERFLOW);
        s.top =s.base +s.stacksize;
        s.stacksize +=STACKINCREMENT;
    }
    *s.top++ =e ;
    return OK;
}

Status Pop(SqStack &s ,SElemType &e){//用e返回删除的这个值
	if(s.top == s.base)return ERROR;
	e = * --s.top;
	return OK;
}

Status StackEmpty(SqStack &s){
if(s.top==s.base)return TRUE;
else return FALSE;
}

void conversion();

int main(){
    conversion();
}

void conversion (){
    int n,m;//数n,进制m
    cin>>n>>m;
    int e;
    SqStack s;
    InitStack(s);

    while(n){
        Push(s,n%m);
        n=n/m;}
        
    while(!StackEmpty(s))
    {
        Pop(s,e);
        printf("%d",e);
    }
}

括号匹配

表达式中含有多种括号，检查括号是否正确嵌套。
思想：设置栈，每读入一个括号，如果是左括号则压入栈，是右括号则与栈顶元素进行匹配，栈结束后如果不空则括号未能完全匹配。

练习

给你一个只包含三种字符的字符串，支持的字符类型分别是 ‘(’、‘)’ 和 ‘'。请你检验这个字符串是否为有效字符串，如果是有效字符串返回 true 。
有效字符串符合如下规则：
任何左括号 ‘(’ 必须有相应的右括号 ‘)’。
任何右括号 ‘)’ 必须有相应的左括号 ‘(’ 。
左括号 ‘(’ 必须在对应的右括号之前 ‘)’。
'’ 可以被视为单个右括号 ‘)’ ，或单个左括号 ‘(’ ，或一个空字符串。
一个空字符串也被视为有效字符串。
示例 1：
输入：s = “()”
输出：true
示例 2：
输入：s = “()"
输出：true
示例 3：
输入：s = "())”
输出：true
提示：
1 <= s.length <= 100
s[i] 为 ‘(’、‘)’ 或 ‘*’

class Solution {
public:
    bool checkValidString(string s) {
        stack<int> star;
        stack<int> left;
        
        for (int i = 0; i < s.size(); i++) {
            char c = s[i];
            if (c == '(') {
                left.push(i);
            }
            if (c == '*') {
                star.push(i);
            }
            if (c == ')') {
                if (!left.empty()) {
                    left.pop();
                } else if (!star.empty()) {
                    star.pop();
                } else {
                    return false;
                }
            }
        }

        while (!left.empty()) {
            int posL = left.top();
            if (star.empty()) return false;
            int posS = star.top();
            if (posS > posL) {
                star.pop();
                left.pop();
            } else {
                return false;
            }
        }

        return true;
    }
};

表达式求值

回文串——用栈解密

回文串是正读反读均相同的字符序列。
思想：回文串关于中间对称，将中点之前的字符入栈，然后依次出栈与中点之后的字符看是否一一匹配，若均能匹配则是回文串。注意串长的偶数与奇数。

gets(a);
len=strlen(a);
mid=len/2-1;
top=0;
for(i=0;i<=mid;i++)
	s[++top]=a[i];
if(len%2==0)
	next=mid+1;
else
	next=mid+2;
for(i=next;i<len-1;i++){
	if(a[i]!=s[top])
		break;
	top--;
}
if(top==0)
	prinf("yes");
else
	prinf("no");

队列

操作受限的线性表。

判断回文

while ((ch = getchar()) != '\n'){
		Push(S,ch);
		EnQueue(q,ch);
	}
	while (!StackEmpty(S)){
		Pop(S,e1);
		DeQueue(q,e2);
		if (e1 != e2) 
		{
			printf("No!!");
			return OK;
		}
	}

猴子分桃

动物园里的n只猴子编号为 1，2，…，n，依次排成一队等待饲养员按规则分桃。动物园的分桃规则是每只猴子可分得m个桃子，但必须排队领取。饲养员循环地每次取出1 个，2 个，…，k个桃放入筐中，由排在队首的猴子领取。取到筐中的桃子数为k 后，又重新从1开始。当筐中桃子数加上队首猴子已取得的桃子数不超过m 时，队首的猴子可以全部取出筐中桃子。取得桃子总数不足m个的猴子，继续到队尾排队等候。当筐中桃子数加上队首猴子已取得的桃子数超过m时，队首的猴子只能取满m个，然后离开队列，筐中剩余的桃子由下一只猴子取用。上述分桃过程一直进行到每只猴子都分到m 个桃子。对于给定的n，k和 m，模拟上述猴子分桃过程。
★数据输入
第 1 行中有 3 个正整数 n，k 和 m，分别表示有 n 只猴子，每次最多取k个桃到筐中，每只猴子最终都分到m个桃子。
★数据输出
将分桃过程中每只猴子离开队列的次序依次输出
输入示例
5 3 40
输出示例
1 3 5 2 4

#include<stdio.h>
#include<stdlib.h>
#include<iostream>
using namespace std;

#define LIST_INIT_SIZE 100
#define LISTINCREMENT 10
#define OK 1
#define ERROR 0
#define OVERFLOW -2

typedef int ElemType;
typedef int DeleteType;
typedef int Status;

//定义链表结点
typedef struct LNode{
	ElemType num;
	ElemType data;
	LNode *next;
}*LinkList;


//链表初始化
Status InitRList(LinkList &L){
	L = (LinkList) malloc (sizeof(LNode));
	if(!L) exit(OVERFLOW);
	L->next = NULL;
	return OK;
}

//创建链表
Status CreateRList(LinkList &L,int n){
	LinkList r = L;
	for (int i = 0; i < n; ++i){
		LinkList q = (LinkList) malloc (sizeof(LNode));
		q->num = i+1;//排编号
		q->data = 0;//桃子数为0
		r->next = q;//放进链表
		r = q;//尾指针更新
	}
	r->next = L->next;
	return OK;
}

int ListLength(LinkList L)
{
	if (L->next == NULL) return 0;
	int i = 0;
	LinkList p = L->next;
	if (p->next == L->next) return 1;
	else{
		p = p->next;
		while(p != L->next)
		{
			i++;
			p=p->next;
		}
	}
	return i+1;
}

//删除链表结点
LinkList DeleteRList(LinkList &L,int m){
	LinkList p,q;
	p = L;
	while (p->next->data != m)
		p = p->next;//p指向桃子数为m的前一个
	q = p->next;//q指向桃子数为m的那个
	p->next = q->next;//将桃子数为m的节点删除
	p = q->next;//p指向更新的节点
	printf("num:%d出列\n",q->num);
	free(q);
	return p;
}

//开始分桃
Status Peaches(int n,int k,int m){//n猴子，最多一次放k，一猴子拿够m
	LinkList L,p;
	InitRList(L);
	CreateRList(L,n);
	p = L->next;
	int temp = 0,cnt = 0,t = 0;//cnt猴子取得的篮里的桃
	//t篮里桃

	while (ListLength(p) > 1){
		if (t) cnt = t;
		else {//重新分发桃
			cnt = temp % k + 1;
			temp++;
		}
		t = 0;//拿走桃子

		if (p->data + cnt < m){
			p->data += cnt;
			p = p->next;
		}
		else {
			t = p->data + cnt - m;
			p->data = m;
			LinkList q = p;
			p = DeleteRList(q,m);

		}
	}
	return p->num;
}

int main(){
	int n,k,m;
	cin>>n>>k>>m;
	printf("num:%d出列\n",Peaches(n,k,m));
	return 0;
}

最简单的队列

利用数组，再加上设置两个指针head,tail构成其基本元素。
出队:head++;
入队:q[tail]=x;tail++;

//封装好的简易queue
struct queue
{
	int data[100];
	int head;
	int tail;
}
struct queue q;
void init_q(queue &q){
	q.head=1;
	q.tail=1;
}
int isfull_q(queue &q){
	if(q.tail>=99)
		return 1;
	else return 0;
}
int isempty_q(queue &q){
	if(q.head<=1)
		return 1;
	else return 0;
}
int insert_q(queue &q,int num)
{
	if(isfull_q(q)!=1)
	{	q.data[q.tail]=num;
		q.tail++;
	}
}
int qout_q(queue &q,int &n)
{
	if(isempty_q(q)!=1)
	{
		n=q.data[q.head];
		q.head++;
	}
}

/*c++ stl库中的queue实现
C++ STL中给出的stack和queue类的声明为：
由stack和queue的声明不难发现，它们本质上并不是容器，而是容器适配器，stack和queue的底层都是调用名为deque（双端队列）的容器的接口来实现的。
所谓适配器，通俗讲就是一种设计模式，即：一套被反复使用的、为多数人所知晓的、经过分类编目的代码设计经验的总结，设计模式可以将一个类接口转换为用户希望的其它类接口。

template <class T, class Container = deque<T>>  class stack;
template <class T, class Container = deque<T>>  class queue;

约瑟夫环（循环队列方法）

N个人围成一圈，第一个人从1开始报数，报M的将被杀掉，下一个人接着从1开始报。如此反复，最后剩下一个，求最后的胜利者。
f(N,M)表示，N个人报数，每报到M时杀掉那个人，最终胜利者的编号
f(N−1,M)表示，N−1个人报数，每报到M时杀掉那个人，最终胜利者的编号
每杀掉一个人，下一个人成为头，相当于把数组向前移动M位。若已知N-1个人时，胜利者的下标位置位f ( N − 1 , M ) 则N个人的时候，就是要加M，因为有可能数组越界，超过的部分会被接到头上，所以还要模N

//f(N,M)=(f(N−1,M)+M)%N
int f(int n,int m) {//递归 
	if(n==1) return 1; 
	return (f(n-1,m)+m)%n; 
}

*双端队列

deque是双端队列容器，它可以同时支持O(1)时间复杂度下的头部的插入删除和在尾部的插入和删除，但无法在O(1)时间复杂度的下实现在中间某个位置插入和删除数据。可以通过下标来访问任意位置处的元素。deque底层空间连续，不需要频繁地申请和释放小块的内存空间，申请和释放空间的消耗相对于list较低，不需要存储每个数据时都存储两个指针来指向前一个和后一个数据的位置。deque扩容时不需要复制数据，而且deque一次开辟一小块空间，空间利用率高。不适合遍历和随机访问，因为deuqe在进行遍历时，迭代器需要频繁地去检查是否移动到了某一小段空间的边界位置，效率低下。

对于vector，它可以支持O(1)时间复杂度下的尾插数据和尾删数据，但要实现头插和头删则需要O(N)的时间复杂度，vector头插和头删数据操作需要移动后面的所有数据，vector在扩容时需用复制已有数据到新的内存空间，并且每次扩容得到新空间的容量一般是原来容量的1.5倍或2倍，vector扩容时复制数据需要一定的消耗且空间浪费相对于deque较多。

对于list，它可以实现在O(1)时间复杂度下任意位置的插入和删除数据，但不能支持通过下标来进行随机访问。
所以，在某种程度上，我们可以认为deque兼具了vector和list的一些优点。

如果没有deuqe容器，那么，stack只能使用vector或list来实现，queue只能使用list来实现。
相对于vector实现stack：deque的扩容代价低，扩容不用拷贝数据，空间浪费较少。
相对于list实现stack：deque不用频繁申请和释放小块内存空间，CPU高速缓存命中率高，申请和释放内存空间的次数少。
相对于list实现queue：deque不用频繁申请和释放小块内存空间，CPU高速缓存命中率高，申请和释放内存空间的次数少。
————————————————
版权声明：本文为优快云博主「【Shine】光芒」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.youkuaiyun.com/weixin_43908419/article/details/129871199

队列+栈综合体

用两个队列实现栈

需要两个队列，需要明确队列操作
.front()/.end()/.dequeue()/.enqueue()/.empty()，
用它们实现栈的push/pop/top/empty操作

思路

入栈操作：将元素压入q1
出栈操作：将q1中除了最后一个元素之外一次出队，压入q2，留下的最后一个元素是出栈元素，再将q2中元素压入q1
判空：如果两个队列都空则栈空

用两个栈实现队列

在这里插入图片描述

练习摆骆驼（纸牌游戏）

扑克牌分成两份，一人一份，a出牌放在桌上，b出牌放在a出的牌的上面，不断交替出牌；直到其中有人出的牌和桌上某张牌牌面相同，则将两张相同的牌及其中所夹牌全部取走并放入自己牌的末尾，当一人手中牌全部出完游戏结束，对方获胜。牌面有1-9；

int book[10]={0};//标记有哪些牌 是否可以赢牌
//创造队列&栈
struct queue{
	int data[1000];
	int head;
	int tail;
};
struct stack{
	int data[10];
	int top;
}
struct queue q1,q2;
struct stack s;
q1.head=1;q1.tail=1;
q2.head=1;q2.tail=1;
s.top=0;
//发牌
for(int i;i<=6;i++){
	scanf("%d",&q1.data[q1.tail++]);
}
for(int i;i<=6;i++){
	scanf("%d",&q2.data[q2.tail++]);
}

void outcards(queue &q,stack &s,int book[]){
	t=q.data[q.head];
	if(book[t]==0){
		q.head++;
		s.data[++s.top]=t;
		book[t]=1;
	}else{
		q.head++;
		q.data[q.tail++]=t;
		while(s.data[s.top]!=t)
		{
			book[s.data[s.top])-=1;
			q.data[q.tail++]=s.data[s.top];
			s.top--;
		}
		book[t]-=1;
		q.data[q.tail++]=t;
		s.top--;
	}
}
void sb_win(int num,queue q,stack s){
	cout<<"player"<<num<<" wins and owns cards including:"<<endl;
	for(i=q.head;i<q.tail;i++){
		printf("%d ",q.data[i]);
	}
	if(s.top>0){
		cout<<"the table has these cards including:"<<endl;
		for(i=1;i<=s.top;i++){
			printf("%d ",s.data[i]);
		}
	}
}

//开始发牌 游戏可能永远无法结束 故最大能玩100局
int round=0;
while(q1.head<q1.tail &&q2.head<q2.tail&&round<100 ){
	round++;
	outcards(q1,s,book);
	if(q1.head==q1.tail) break;
	outcards(q2,s,book);
	//同上，t2继续出牌
}
if(round==100) return 0;//程序结束
if(q1.head==q1.tail)sb_win(1,queue q2,stack s)；
else sb_win(2,queue q1,stack s)；

数组和广义表

求两数组交集

打印出来不仅要打印交集，还要与两个数组中交集元素出现的次数一致。
如num1=[1,2,2,1];num2=[2,2]打印[2,2]
思路：首先第一步分别排好序，然后准备两个指针i,j分别属于两个数组，
if a[i]<b[j]:i++
if a[i]>b[j]:j++
if a[I]==b[j]: {vector.push_back(a[i]);i++;j++}

如果num1比num2大小少很多，怎么处理？
先用二分法得到一个更小的区间，再用上述方法。
如果内存一次仅能放入n个元素，不能一次加载所有元素进入内存，怎么处理？
这里就涉及到外部归并排序，排序成多个临时文件，将每个文件的前n1大小的数据放入输入缓冲区，利用分割好的内存作为输出缓冲区，执行k路归并算法将结果输出到输出缓冲区，当输出缓冲区满则写入（push_back）磁盘目标文件，清空缓冲区直至所有数据归并完成；利用两个队列，分别放入num1,num2部分元素，加载满后按照原方法比对，用完则出队，依次放入接下来的部分元素。

稀疏矩阵三元组的运算

打印转置矩阵

求转置并按行优先排序算法：即按原矩阵列的先后顺序排在行数一栏

void transpose(int a[][3],int b[][3]){
	int p,q,col;
	b[0][0]=a[0][0];//非0元素个数
	b[0][1]=a[0][2];
	b[0][2]=a[0][1];
	if(b[[0][0]>0){
		q=1;
		for(col=0;col<b[0][1];++col)
			for(p=1;p<=b[0][0];++p)
				if(a[p][2]==col){
					b[q][0]=a[p][0];
					b[q][1]=a[p][2];
					b[q][2]=a[p][1];
					++q;
				}
	}
}
void TransMatrix(TMatrix a , TMatrix b)
{   int p , q , col ;
	b.rn=a.cn ;  b.cn=a.rn ;  b.tn=a.tn ;
/*    置三元组表b.data的行、列数和非0元素个数 */
if  (b.tn==0)    printf(“ The Matrix A=0\n” );
else
{   q=0;/*   每循环一次找到转置后的一个三元组  */
	for  (col=1; col<=a.cn ; col++)
		for  (p=0 ;p<a.tn ; p++) /*   循环次数是非0元素个数   */
             if  (a.data[p].col==col)
            {  b.data[q].row=a.data[p].col ;
               b.data[q].col=a.data[p].row ; 
               b.data[q].value=a.data[p].value; 
               q++ ;
           }
}
}

在方法一基础上改进：附设两个辅助向量num[ ]和cpot[ ] 。
◆ num[col]：统计A中第col列中非0元素的个数；
◆ cpot[col] ：指示A中第一个非0元素在b.data中的恰当位置。Cpot[1]=1因为第一列的第一个元素必须要放在转置后的三元组的第一行，第0行未使用。则下一列第一个元素的位置就是上一列所有元素放完后的下一个位置。Cpot[col]=cpot[col-1]+num[col-1];
辅助向量cpot[ ]固定在稀疏矩阵的三元组表中用来指示每行第一个非0元的位置，便于随机存取任何一行非0元。将这个辅助向量放入结构体中作为rpos[]数组，这种带行链接信息的三元组表成为“行逻辑链接的顺序表”，见后面代码

void  FastTransMatrix(TMatrix a, TMatrix b)
{   int p , q , col , k ;
	int num[MAX_SIZE] , copt[MAX_SIZE] ;
	b.rn=a.cn ; b.cn=a.rn ; b.tn=a.tn ;
	/*   置三元组表b.data的行、列数和非0元素个数  */ 
if  (b.tn==0)    printf(“ The Matrix A=0\n” ) ;
else
{   for (col=1 ; col<=a.cn ; ++col)    num[col]=0 ;//向量num[]初始化为0   
    for (k=1 ; k<=a.tn ; ++k) ++num[a.data[k].col] ;//求原矩阵中每一列非0元素个数
	for (cpot[0]=1, col=2 ; col<=a.cn ; ++col)
    	cpot[col]=cpot[col-1]+num[col-1];/*求第col列中第一个非0元在b.data中的序号 */
	for (p=1 ; p<=a.tn ; ++p)
    {  	col=a.data[p].col;
    	q=cpot[col];
       	b.data[q].row=a.data[p].col ;
       	b.data[q].col=a.data[p].row ;
       	b.data[q].value=a.data[p].value ; 
       	++cpot[col] ;/*至关重要!!当本列中下一个元素直接放到这个下标中  */
     }
}
}

行逻辑链接的三元组顺序表

b.rpos[row]指示了矩阵B的第row行中第一个非0元素在b.data[ ]中的位置(序号)，b.rpos[row+1]-1指示了第row行中最后一个非0元素在b.data[ ]中的位置(序号) 。

typedef struct  
{   Triple data[MAX_SIZE] ;     /*  非0元素的三元组表  */  
	int rpos[MAX_ROW];     /* 各行第一个非0位置表 */ 
	int    rn ,cn , tn ;       /*  矩阵的行、列数和非0元个数  */
}RLSMatrix ;

在这里插入图片描述

稀疏矩阵相加和相乘

A(m1n1) 与B(n1n2)相乘
在稀疏矩阵里如何相乘？将m.data中的j与n.data中的i值相等的元素乘起来，如果有多个乘积则相加，值不为0的放入新三元组。

void add(int a[][3],int b[][3],int c[][3]){//3元组相加
	int i=1,j=1,k=1,m;
	while(i<=a[0][0]&&j<=b[0][0])
	if(a[i][1]==b[j][1])
	{
		if(a[i][2]<b[j][2]){
			c[k][0]=a[i][0];
			c[k][1]=a[i][1];
			c[k][2]=a[i][2];
			k++;
			i++;
		}else if(a[i][2]>b[j][2]){
			c[k][0]=b[j][0];
			c[k][1]=b[j][1];
			c[k][2]=b[j][2];
			k++;
			j++;
		}else{
			m=a[i][0]+b[j][0];
			if(m!=0){
				c[k][1]=a[i][1];
				c[k][2]=a[i][2];
				c[k][0]=m;
				k++;
			}
			i++;j++;
		}
	}else if(a[i][1]<b[j][1]){
			c[k][0]=a[i][0];
			c[k][1]=a[i][1];
			c[k][2]=a[i][2];
			k++;
			i++;
	}else{
			c[k][0]=b[j][0];
			c[k][1]=b[j][1];
			c[k][2]=b[j][2];
			k++;
			j++;
	}
	while(i<=a[0][0]){
			c[k][0]=a[i][0];
			c[k][1]=a[i][1];
			c[k][2]=a[i][2];
			k++;
			i++;
	}
	while(i<=b[0][0]){
			c[k][0]=b[j][0];
			c[k][1]=b[j][1];
			c[k][2]=b[j][2];
			k++;
			j++;
	}
	c[0][0]=k-1;//非0元素个数
	c[0][1]=a[0][1];
	c[0][2]=a[0][2];
}

//最基本的矩阵相乘
for(i=1;i<=m1;++i)
	for(j=1;j<=n2;++j){
		q[i][j]=0;
		for(k=1;k<=n1;++k)q[i][j]+=a[i][k]*b[k][j];
	}

//3元组相乘
int getvalue(int d[][3],int i,int j){//从原稀疏矩阵中找出来i行j列的值
	int k=1;
	while(k<=d[0][0]&&(d[k][1]!=i||d[k][2]!=j))k++;
	if(k<=d[0][0])return d[k][0];
	else return 0;
}
void mul(int a[][3],int b[][3],int c[][3],int m,int n,int k){
	int i,j,l,1,s;
	for(i=0;i<m;i++)
		for(j=0;j<k;j++){
			s=0;
			for(l=0;l<n;l++)
				s+=getvalue(a,i,l)*getvalue(b,l,j);
			if(s!=0){
				c[p][1]=i;
				c[p][2]=j;
				c[p][0]=s;
				++p;
			}
		}
	c[0][1]=m;
	c[0][2]=k;
	c[0][0]=p-1;
}

vector

vector容器的功能和数组非常相似，使用时可以把它看成一个数组
vector和普通数组的区别：
1.数组是静态的，长度不可改变，而vector可以动态扩展，增加长度
2.数组内数据通常存储在栈上，而vector中数据存储在堆上

动态扩展：(这个概念很重要)
动态扩展并不是在原空间之后续接新空间，而是找到比原来更大的内存空间，将原数据拷贝到新空间，释放原空间

注意：使用vector之前必须包含头文件 #include < vector>

1.构造
void TestVector()
{
    vector<int> v1;  //无参构造
    vector<int> v2(3, 0); //用3个0去初始化
    vector<int> v3(v1); //拷贝构造
    vector<int> v4(v1.begin(), v1.end()); //迭代器区间构造
}
2.判空、查询/修改大小，容量，清除
void text03()
{
	vector<int> v1;
	cout << v1.empty() << endl;
    cout << v1.size() << endl; //17
    cout << v1.capacity() << endl;//不同编译编译器的扩容机制不一样，因此空间的大小不一定
    v1.clear(); //调用clear
	//重新指定容器大小使其变长
	v1.resize(10);       //调用4，增加的长度默认值为0（不指定情况下默认为0）
	v1.resize(15, 9);    //调用5，增加的长度赋值为9
	//重新指定容器大小使其变短
	v1.resize(10);       //调用4，删除了上一步中最后赋值为9的5个长度
	v1.resize(5);     //调用5，删除了上一步中默认值为0的5个长度

}

3.赋值、插入、删除
void text02()
{
	vector<int> v1,v2;
	for (int i = 0; i < 5; ++i)
	{
		v1.push_back(i);
	}
	v2 = v1;                        //调用1，赋值运算符重载
	vector<int> v3,v4;
	v3.assign(v1.begin(), v1.end());//调用2，区间赋值
	v4.assign(5, 9);                //调用3，放入5个9
}
void text04()
{
	vector<int> v1;
	v1.push_back(6);//调用1，尾部插入元素6
	v1.pop_back();//调用2，删除最后一个元素
	v1.insert(v1.begin(),20);//调用3，在首位插入20
	v1.insert(v1.end(), 3, 20);//调用4，在尾部插入3个20
	v1.erase(v1.begin()); //调用5，在首位删除一个元素
	v1.erase(v1.begin(),v1.end()); //调用6，删除首位到末尾所有元素，也就是删除全部元素
	v1.clear();//调用7，清空所有元素

	v1.swap(v2);   //调用互换函数，容器v1,v2互换
}
4.查询数据
void text05()
{
	for (int i = 0; i < v.size(); ++i)
	{
		cout << v.at(i) << " ";//调用1
	}

	//利用[]访问v
	for (int i = 0; i < v.size(); ++i)
	{
		cout << v[i] << " ";//调用2
	}
	
	cout << "容器中第一个元素是：" << v.front() << endl;//调用3
	cout << "容器中最后一个元素是：" << v.back() << endl;//调用4
}

5.迭代器操作
void TestVector()
{
    vector<int> v1(10, 1);
    vector<int>::iterator vt = v1.begin();//rbegin,rend反向起止迭代器
    while (vt != v1.end())
    {
        cout << *vt << " ";
        ++vt;
    }
}

练习：杨辉三角1

给出非负整数n，生成杨辉三角前n行
采用可变容器vector比较方便

vector<vector<int>> r(n);
for(int i=0;i<n;i++){
	r[i].resize(i+1);
	r[i][0]=r[i][i]=1;
	for(int j=1;j<i;j++)
		r[i][j]=r[i-1][j-1]+r[i-1][j];
}
return r;
//若只需要输出某行，return r[i]
//优化到空间复杂度为o(k)的输出某行杨辉三角：直接在原数组上替换
vector<int> ri(n+1);
ri.assign(n+1, 0);  //放入n+1个0  
ri[0]=1;
for(int i=0;i<=n;i++){
	for(int j=i;j>0;j--)
		ri[j]=ri[j]+ri[j-1];//从右往左依次相邻两个相加
}
return ri;

杨辉三角重要性质

每行头尾数为1
上行两数之和生成下行新元素
第n行有n项数字
第n行第m个数表示组合数c(n-1,n-1)；由组合数性质也可得到第n行第m个数和第n-m+1个数相同
(a+b)^n展开式的系数对应杨辉三角第n+1行每一项

练习：求最小三元组的距离

【2020 408真题】
已知三个升序整数数组a[l], b[m]和c[n]。请在三个数组中各找一个元素，是的组成的三元组距离最小。三元组的距离定义是：假设a[i]、b[j]和c[k]是一个三元组，那么距离为:
Distance = max(|a[ I ] – b[ j ]|, |a[ I ] – c[ k ]|, |b[ j ] – c[ k ]|)
请设计一个求最小三元组距离的最优算法，并分析时间复杂度。
最简单的是三重循环暴力。
优化思路：根据三元组定义，显然三个数字最接近时，得到的距离最小。
不妨假设a【i】<=b【j】<=c【k】。
分三种情况：
1）第一种移动a【i】，若有a【i】<=b【j】<=c【k】或者b【j】<=a【i】<=c【k】，此时最小距离更新；若移动后的a【i】>=c【k】，此时最短距离不变或者刷新。
2）第二种移动b【j】，若有a【i】<=b【j】<=c【k】之间，则最短距离不变；若移动后的b【j】>=c【k】，则最短距离不变。————这种做法不可能刷新最小距离，不可取。
3）第三种移动c【k】，和第一种移动同理，故暂定按第一种移动。

当某一个数组遍历完成时，便会得到最小三元组距离。时间复杂度O（l+m+n）。

#include<bits/stdc++.h>
using  namespace std;
const int maxn=10010;
const int inf=0x7fffffff;
int a[maxn],b[maxn],c[maxn];
int main(){
	int m,n,l;
	cin>>m>>n>>l;
	for(int i=0;i<m;i++) cin>>a[i];
	for(int i=0;i<n;i++) cin>>b[i];
	for(int i=0;i<l;i++) cin>>c[i];
	int i=0,j=0,k=0;
	vector<int>v1,v2,v3;//保存最小dis的三元组序列 
	int dis=inf;
	while(1){
		if(i==m || j==n || k==l) break;
		int temp=abs(a[i]-b[j])+abs(a[i]-c[k])+abs(b[j]-c[k]);
		if(temp<dis){
		    dis=temp;	
			v1.clear();v1.push_back(a[i]);
			v2.clear();v2.push_back(b[j]);
			v3.clear();v3.push_back(c[k]);
		}else if(temp==dis){ //保存这种最小dis的可能下标
			v1.push_back(a[i]);
			v2.push_back(b[j]);
			v3.push_back(c[k]);
		} 
		if(a[i]<=b[j] && a[i]<=c[k]) i++;//继续往右移动最小的下标探索下一种min可能
		else if(b[j]<a[i] && b[j]<c[k]) j++;
		else k++;
	}
	cout<<dis<<endl; 
	for(int i=0;i<v1.size();i++){
		cout<<v1[i]<<" "<<v2[i]<<" "<<v3[i]<<endl;
	}
	return 0;
}

树和二叉树

树是不包含回路的连通无向图。
一棵树中任意两个节点有且仅有唯一一条路径连通。
一棵树如果有n个节点则一定恰好有n-1条边。
在一棵树中不加节点而加一条边必然构成回路。
根节点：没有根节点的节点
叶节点：没有子节点的节点
内部节点：既不是根节点，也不是叶节点
二叉树：要么为空树，要么每个节点最多有两棵子树，子树分别是一棵二叉树。
满二叉树：二叉树每个内部节点都有两个孩子，有2^（h-1）个节点。存储它是非常方便的，直接一维数组都能存，父节点编号k，左孩子2k,右孩子2k+1.
完全二叉树：除了最后一层之外其他层都是最大节点个数且如果一个节点有右子节点则必有左子节点。有n个节点则高度为以2为底的logn

//构建二叉树 方法1
#define MAX_NODE  50
typedef struct BTNode
{  	char  data ;
	struct BTNode *Lchild , *Rchild ;
}BTNode ;
BTNode  *Create_BTree(void)   
  /*   建立链式二叉树，返回指向根结点的指针变量  */
{  	BTNode  *T , *p , *s[MAX_NODE] ;  
	char ch ; int i , j ;
	while (1)
	{  	scanf(“%d”, &i) ;
		if  (i==0)  break ;   /*  以编号0作为输入结束  */
		else  
	     	{  	ch=getchar() ;
	       		p=(BTNode *)malloc(sizeof(BTNode)) ;
	       		p–>data=ch ;
	       		p–>Lchild=p–>Rchild=NULL ;  s[i]=p ;
	       		if (i==1)  T=p ; 
	       		else 
	           	{  j=i/2 ;    /*    j是i的双亲结点编号  */
	               if (i%2==0)  s[j]->Lchild=p ;
	               else  s[j]->Rchild=p ;
	            }
	   		}
	}
	return(T) ;
}
//构建二叉树 方法2
#define NULLKY  ‘?’
#define MAX_NODE   50
typedef struct BTNode
{  	char  data ;
	struct BTNode *Lchild , *Rchild ;
}BTNode ;
BTNode  *Preorder_Create_BTree(BTNode  *T)
 /*   建立链式二叉树，返回指向根结点的指针变量  */
{  	char ch ; 
	ch=getchar() ; getchar(); 
	if  (ch==NULLKY) 
	{    T=NULL;  return(T) ;  }
	else
	{  T=(BTNode *)malloc(sizeof(BTNode)) ;
		T–>data=ch ;
		Preorder_Create_BTree(T->Lchild) ;
		Preorder_Create_BTree(T->Rchild) ;
		return(T) ; 
	}
}
//当希望创建上述算法所得二叉树时，输入的字符序列可以是：
//ABD??E?G??CF???

并查集

运用一维数组实现，本质是维护一个森林，刚开始每个点都是孤立的，每个点都是一棵只有一个节点的数，后面慢慢合并（遵循靠左原则，擒贼先擒王原则）。
找到最高祖先即祖宗才能判断两个节点是否是一个根节点。

以下是路径压缩示意图：
在这里插入图片描述

//yanbook版
typedef pTree MFSet;
int find_mfset(MFSet s,int i){//时间复杂度o(d)d树的高度
	if(i<1||i>s.n)return -1;
	for(j=i;s.nodes[j].parent>0;j=s.nodes[j].parent);
	return j;
}
status merge(MFSet &s,int i,int j){//时间复杂度o(1)
	if(i<1||i>s.n||j<1||j>s.n)return error;
	s.nodes[i].parent=j;
	return ok;
}
//改进1:小合入大
void fix_1(MFSet &s,int i,int j){
	if(i<1||i>s.n||j<1||j>s.n)return error;
	if(s.node[i].parent>s.nodes[j].parent){
	//根节点数组值均为负，其绝对值为成员个数
		s.node[j].parent+=s.node[i].parent;
		s.node[i].parent=j;
	}else{
		s.node[i].parent+=s.node[j].parent;
		s.node[j].parent=i;
	}
	return ok;
}
//改进2：压缩路径,将根节点到i上所有节点都变为根的孩子节点
int fix_2(MFSet &s,int i){
	if(i<1||i>s.n)return error;
	for(j=i;s.nodes[j].parent>0;j=s.nodes[j].parent);
	for(k=i;k!=j;k=t){
		t=s.nodes[k].parent;
		s.nodes[k].parent=j;
	}
	return j;
}
//aha版
#include <stdio.h>   
int f[1001]={0},n,m,sum=0;   
//初始化，数组里面存的是自己数组下标的编号就好了。   
void init()   
{   
    int i;   
    for(i=1;i<=n;i++)   
        f[i]=i;  
    return;
}   
 
//这是找爹的递归函数，不停地去找爹，直到找到祖宗为止，其实就是去找最高领导，“擒贼先擒王”原则。
int getf(int v) 
{   
    if(f[v]==v)   
        return v;   
    else  
    {   /*这里是路径压缩，每次在函数返回的时候，
    顺带把路上遇到的人的“BOSS”改为最后找到的祖宗编号，这样可以提高今后找到最高领导（树的祖先）的速度*/
        f[v]=getf(f[v]);//这里进行了路径压缩
        return f[v];   
    }   
 
}   
 
//这里是合并两子集合的函数
void merge(int v,int u) 
{   
    int t1,t2;//t1、t2分别为v和u的大BOSS
    t1=getf(v);
    t2=getf(u);
    if( t1!=t2 ) //判断两个结点是否在同一个集合中，即是否为同一个祖先。
    {  
        f[t2]=t1;
      //“靠左”原则，左边变成右边的BOSS。即把右边的集合，作为左边集合的子集合
    }
    return;
}   
int main() 
{     
    int i,x,y; 
    scanf("%d %d",&n,&m); 
    init();  //初始化是必须的 
    for(i=1;i<=m;i++)   
    { 
        scanf("%d %d",&x,&y);   
        merge(x,y);   
    }
    for(i=1;i<=n;i++)
    {
        if(f[i]==i) sum++;
    }
    printf("%d\n",sum);//输出有多少个集合
    return 0;   
}

先序遍历/中序遍历/后序遍历/层次遍历

有递归和非递归版本，当然非递归版本是将系统栈换成自己定义的栈。

在遍历序列中，后序遍历的非递归算法的操作过程中，借用了栈的操作。重要特性：在遍历到某结点时，算法栈内的元素就是其祖先结点，且按栈顶到栈底顺序是父结点一直到根结点。

后序遍历也可借助先序遍历+两个栈来得到，后序遍历=先序遍历序列逆置+原树左右子树位置对换。

//递归
void  PreorderTraverse(BTNode  *T)//先序
{  if  (T!=NULL) 
	{	visit(T->data) ;       /*  访问根结点  */
		PreorderTraverse(T->Lchild) ;
		PreorderTraverse(T->Rchild) ;     
	}
}
void  InorderTraverse(BTNode  *T)//中序
{   if  (T!=NULL) 
	{  	InorderTraverse(T->Lchild) ;
		visit(T->data) ;       /*   访问根结点   */
		InorderTraverse(T->Rchild) ;
	}
} 
void  PostorderTraverse(BTNode  *T)//后序
{   if  (T!=NULL) 
	{   PostorderTraverse(T->Lchild) ;
		PostorderTraverse(T->Rchild) ; 
		visit(T->data) ;       /*  访问根结点  */ 
	}
} 

//非递归
void PreOrder(BiTree T)
{
	Stack<BiTree> S;
	BiTNode *p;
	P=T;
	While(p||!s.empty()){
	if(p){
		Visit(p);
		S.push(p);
		P=p->lchild;
	}else{//p为空时则可以开始访问右节点了
		P=s.top();
		s.pop();
		P=p->rchild;
		}
	}
}
//二叉树中序遍历的非递归算法
#define stacksize 20
#include<stack>
void inorder(BiTree T)
{
    stack<BiTNode> S;
    BitNode * p=T;                       //p作为遍历指针
    while(p!=NULL || !S.empty())
    {
        while(p!=NULL)                  //遍历左子女结点
        {
            S.push(p);
            p=p->lchild;
        }
        if(!S.empty())                         //栈不空时退栈
        {       p=S.top();
				S.pop();
                visit(p);
                p=p->rchild;	    //遍历指针进到右子女节点
        }
    }
}
//二叉树非递归后序遍历
//需要增加一个结点r来保存最近访问节点,从而区分是否访问过左或右子树
void postorder(Bitree T)
{
    Stack<BiTNode> S;
    BitNode * p =T, *pre=NULL; //p为遍历指针,pre是前趋指针
    while(p!=NULL || !S.empty())
    {
        while(p!=NULL)                        //左子树进栈
        {
			S.push(p);
			p=p->lchild;
        }
        if(!S.empty())
        {
            p=S.top();          //用p记忆栈顶
            if(p->rchild!=NULL && p->rchild!=pre)
				p=p->rchild;        //p有右子女且未访问过
            else
            {
				visit(p);
				pre=p;p=NULL;       //记忆刚访问过的结点
                S.pop();
            }
        }
}}
/*另一种方法：
当搜索指针指向某一根结点时，不能立即访问，而要先遍历其左子树，此时根结点进栈。
当其左子树遍历完后再搜索到该根结点时，还是不能访问，还需遍历其右子树。
所以，此根结点还需再次进栈，当其右子树遍历完后再退栈到到该根结点时，才能被访问。
因此，设立一个状态标志变量tag ：tag=0暂时不可访问，tag=1可以访问。
设两个堆栈S1、S2 ，S1保存结点，S2保存结点的状态标志变量tag 。
S1和S2共用一个栈顶指针。
设T是指向根结点的指针变量。
非递归算法是：
若二叉树为空，则返回；否则，令p=T；
⑴ 第一次经过根结点p，不访问：p进栈S1 ，tag 赋值0并进栈S2，p=p->Lchild 。
⑵ 若p不为空，转(1)，否则，取状态标志值tag ：
⑶ 若tag=0：对栈S1，不访问，不出栈；修改S2栈顶元素值(tag赋值1) ，
	取S1栈顶元素的右子树，即p=S1[top]->Rchild ，转(1)；
⑷ 若tag=1：S1退栈，访问该结点；
直到栈空为止。*/
void  PostorderTraverse( BTNode  *T)
{   BTNode  *S1[MAX_NODE] ,*p=T ;
	int S2[MAX_NODE] , top=0 , bool=1 ;
	if  (T==NULL)  printf(“Binary Tree is Empty!\n”) ;
	else  
	{ do{ 
	     	while (p!=NULL)
	              {  S1[++top]=p ; 
					 S2[top]=0 ; 
	                 p=p->Lchild ;   			
	              }
	          if  (top==0)  bool=0 ;
	          else if  (S2[top]==0)
	          {  p=S1[top]->Rchild ;  
	          	 S2[top]=1 ;   }
	          else 
	          { p=S1[top] ; top-- ;
	          	visit( p->data ) ; 
	          	p=NULL ;}
		}while (bool!=0) ;
	}
}
//二叉树后序遍历（两个栈实现版）
void post_order(btnode *bt){
	if(bt!=NULL)
	{
		btnode *stack1[maxsize];int top1=-1;
		btnode *stack2[maxsize];int top2=-1;
		btnode *p=NULL;
		stack1[++top1]=bt;
		while(top1!=-1){
			p=stack1[top1--];
			stack2[++top2]=p;
			//先左后右，这样经stack2转换后变成先右后左即可
			if(p->lchild!=NULL)stack1[++top1]=p->lchild;
			if(p->rchild!=NULL)stack1[++top1]=p->rchild;
		}
		while(top2!=-1){
			p=stack2[top2--];
			visit(p);
		}
	}
}
//二叉树非递归层序遍历
Void levelorder(BiTree T){
	Quene<BiTNode> Q;
	Q.push(T);
	BiTNode *p=T;
	if  (p!=NULL) 
	{
		While(!Q.empty()){
			p=Q.front();
			Q.pop();
			Visit(p);
			If(p->lchild)Q.push(p->lchild);
			If(p->rchild)Q.push(p->rchild);
		}
	}
}

练习：按先序序列建立二叉树

先序序列中其中不存在的节点用’ '表示。

status create_bitree(bitree &t){
	scanf(&ch);
	if(ch==' ')t=NULL;
	else{
		if(!(t=(biTnode *)malloc(sizeof(biTnode))))return overflow;
		t->data=ch;
		create_bitree(t->lchild);
		create_bitree(t->rchild);
	}
	return ok;
}

练习：以先序输出一棵二叉树所有节点数据值及层次

Void printfirst(BiTree *T,int level){
	If(T){
		Printf(“data=%d,level=%d”,T->data,level);
		If(T->left)Printfirst(T->left,level+1);
		If(T->right)Printfirst(T->right,level+1);
	}
	return;
}
Int main(){
	Init(T);
	Printfirst(T,1);
}

练习：根据先序序列、中序序列构造二叉树

先序遍历序列存储在一维数组pre[l1,…r1]中，中序遍历序列存储在一维数组in[l2,…r2]中，构造该二叉树。

btnode *createbt(char pre[],char in[],int l1,int r1,int l2,int r2){
	btnode *s;
	int i;
	if(l1>r1)return NULL;
	s=(btnode *)malloc(sizeof(btnode));
	s->lchild=s->rchild=NULL;
	for(i=l2;i<=r2;i++){
		if(in[i]==pre[l1])break;
	}
	s->data=in[i];
	s->lchild=createbt(pre,in,l1+1,l1+i-l2,l2,i-1);
	s->rchild=createbt(pre,in,l1+i-l2+1,r1,i+1,r2);
	return s;
}

练习：二叉树剪枝

给一棵二叉树，节点值要么是0，要么是1。剪掉那些只含0的子树。

node* prune_tree(node *root){
	if(root==NULL)return root;
	root->left=prune_tree(root->left);
	root->right=prune_tree(root->right);
	if(root->left!=NULL||root->right!=NULL||root->val==1)return root;
	return NULL;
}

练习：判断两棵二叉树是否相似

试设计判断两棵二叉树是否相似的算法，所谓二叉树t1和t2是相似的指的是t1和t2都是空的二叉树；或者t1和t2的根结点是相似的，t1的左子树和t2的左子树是相似的且t1的右子树与t2的右子树是相似的。

int like(BTNode *b1, BTNode *b2)
    { 
    	int like1, like2;
    	if (b1==NULL && b2==NULL) 
        	    return 1;
    	else if (b1==NULL || b2==NULL) 
        	    return 0;
    	else
    	{       like1=like(b1->lchild, b2->lchild);
        	    like2=like(b1->rchild, b2->rchild);
        	    return (like1 & like2);
  	}
}

练习：判断是否是对称二叉树

判断是否是镜像对称的。首先它们要相似，其次它们每个节点的值相同。

bool is_symmetric(node *root1,node *root2){
	if(!root1&&!root2)
		return true;
	else if(root1!=NULL&&root2!=NULL){
		if(root1->val==root2->val)
			return is_symetric(root1->left,root2->right)&&is_symetric(root1->right,root2->left);
		else return false;
	}else return false;
}
bool judge_main(node *root){
	if(!root)return true;
	return is_symmetric(root->left,root->right);
}

由此可延伸出变形练习：判断两棵树是否完全相同

bool is_symmetric(node *root1,node *root2){
	if(!root1&&!root2)
		return true;
	else if(root1!=NULL&&root2!=NULL){
		if(root1->val==root2->val)
			return is_symetric(root1->left,root2->left)&&is_symetric(root1->right,root2->right);
		else return false;
	}else return false;
}

继续延伸出变形练习：合并二叉树
当两个二叉树节点重叠时，它们的值相加作为节点合并后的新值，否则不为空的节点将直接作为新二叉树的节点。

void merge(node *&root1,node *root2){
	if(!root1&&!root2)
		return;
	else if(root1!=NULL&&root2!=NULL)root1->val+=root2->val;
	else if(root2!=NULL)root1=root2;
	merge(root1->left,root2->left);
	merge(root1->right,root2->right);
}

练习：将表达式树转换为等价的中缀表达式，用括号表示计算次序

考点：中序遍历。
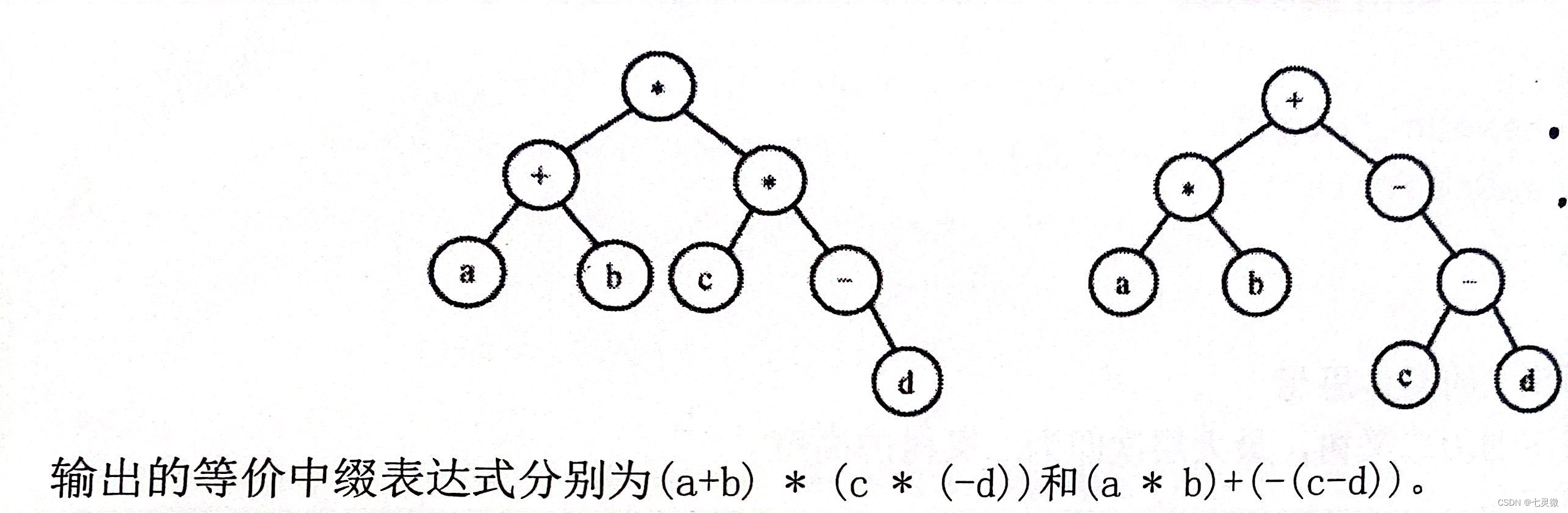
在这里插入图片描述
思想难点在于什么时候加括号？当深度大于1时就要在最前面加左括号，最后面加右括号。

string res="";
void  InorderTraverse(BTNode  *T,int deep)//中序
{   if  (T!=NULL) 
	{  	if(p->left==NULL&&p->right==NULL)
			res+=p->data;
		else{
			if(deep>1)res+='(';
			InorderTraverse(T->Lchild,deep+1);
			res+=p->data;
			InorderTraverse(T->Rchild,deep+1);
			if(deep>1)res+=')';
			}
	}
} 
InorderTraverse(root,1);

练习：交换左右子树/翻转二叉树

node* invert(node *root){
	if(root!=NULL){
		node *tmp=root->left;
		root->left=root->right;
		root->right=tmp;
		invert(root->left);
		invert(root->right);
	}
	return root;
}

练习：统计二叉树中度为0，1，2的节点个数

int degree0=0,degree1=0,degree2=0;
void count(node *root){
	if(root==NULL)
		return;
	if(root->left!=NULL&&root->right!=NULL){
		degree2++;
		count(root->left);
		count(root->right);
	}else if(root->left!=NULL){
		degree1++;
		count(root->left);
	}else if(root->right!=NULL){
		degree1++;
		count(root->right);
	}else{
		degree0++;
		return;
	}
}

练习：从二叉树中删去所有叶节点

void DeleteLev(BiTree T,BiTree f,bool flag){ 
//要记录父节点以及该节点是左孩子/右孩子 flag为true左孩子 false右孩子 
    if(T){//T is not NULL
        if(T->l)DeleteLev(T->l,T,true);
        else if(T->r)DeleteLev(T->r,T,false);
        else{//无子女为叶子节点
            free(T);
            if(f){// T is not root
                if(flag)f->l = NULL;
                else f->r = NULL;
        	}
		}
}
void main(){
    Init(T);
    DeleteLev(T,NULL,true);
}

练习：求叶子结点数

假设二叉树采用二叉链表存储结构，设计一个算法求其指定的某一层k（k>1）的叶子结点个数，要求：
(1）给出算法的基本设计思想。
(2）写出二叉树采用的存储结构代码
(3）根据设计思想，采用C或C+语言描述算法，关键之处给出注释。
使用层次遍历模型，只需要记录当前层数（以知是否达到目标层数）即可。
在到达目标层数前，正常层次遍历即可。
到达目标层数后，停止遍历，那么当前队列内的所有元素就是这一层的所有结点。对其进行逐个判断是否是叶结点即可。

//二叉树求叶子结点个数
int  search_leaves( BTNode  *T)
{	BTNode  *Stack[MAX_NODE] ,*p=T;
	int  top=0, num=0;
	if  (T!=NULL)
	{  stack[++top]=p ; 
		while (top>0)
	   	 {   p=stack[top--] ;
	       	if (p->Lchild==NULL&&p->Rchild==NULL)  
	       		num++ ;   
	        if  (p->Rchild!=NULL )
	             stack[++top]=p->Rchild; 
	        if  (p->Lchild!=NULL )
	                stack[++top]=p->Lchild; 
	     }
	}
	return(num) ;
}

练习：求层序遍历变形：自上而下，自右向左

栈的应用

练习：求二叉树最小深度

最小深度：根节点到最近叶子结点最短路径上的节点数量。

int find_minlen(node *p){
	if(!p)return 0;
	if(p->left==NULL&&p->right==NULL)return 1;
	else if(p->left==NULL)return 1+find_minlen(p->right);
	else if(p->right==NULL)return 1+find_minlen(p->left);
	else return 1+min(find_minlen(p->left),find_minlen(p->right));
}

练习：返回二叉树高度

//求二叉树深度
//层次遍历，该方法为记录每一层的的个数，当一层全部出队列 层数+1
int  search_depth( BTNode  *T)
{  	BTNode  *Stack[MAX_NODE] ,*p=T;
	int  front=0 , rear=0, depth=0, level ;
	/*  level总是指向访问层的最后一个结点在队列的位置  */
	if  (T!=NULL)
	{  Queue[++rear]=p;    /*   根结点入队  */
		level=rear ;    /*  根是第1层的最后一个节点  */
		while (front<rear)
	     	{  	p=Queue[++front]; 
	         	if (p->Lchild!=NULL)
	               Queue[++rear]=p->Lchild;    /*   左结点入队  */
	         	if (p->Rchild!=NULL)
	               Queue[++rear]=p->Rchild;    /*   左结点入队  */
	          	if (front==level)  
	             /*  正访问的是当前层的最后一个结点  */
	             {  depth++ ;  level=rear ;  }
	      }
	}
}
//递归版
int Height(BiTree T)
{
	if(T==NULL)
		return 0;
	Hl=Height(T->left);
	Hr=Height(T->right);
	if(Hl>Hr)
		return Hl+1;
	else
		return Hr+1;
}

练习：是否为完全二叉树的判断

算法思路：层序遍历，遇到空节点时查看其后是否还有非空节点，若有则二叉树不是完全二叉树。

bool is_complete(bitree t){
	initqueue(q);
	if(!t)return 1;
	enqueue(q,t);
	while(!isempty(q)){
		dequeue(q,p);
		if(p){
		//不用考虑是不是空，因为要检查所有节点找出第一个空节点
			enqueue(q,p->lchild);
			enqueue(q,p->rchild);
		}else{
			while(!isempty(q)){
				dequeue(q,p);
				if(p)return 0;
			}
		}
	}
}

练习：求值为x的节点的层数

递归或者层次遍历

//递归
int l=1;
void leno(btnode *p,char x){
	if(p!=NULL){
		if(p->data==x)cout<<l<<endl;
		++l;
		leno(p->lchild,x);
		leno(p->rchild,x);
		--l;//返回上一层时要减
	}
}
//对求二叉树深度的变形
int  search_depth( BTNode  *T)
{  	BTNode  *Stack[MAX_NODE] ,*p=T;
	int  front=0 , rear=0, depth=1, level ;
	/*  level总是指向访问层的最后一个结点在队列的位置  */
	if  (T!=NULL)
	{  Queue[++rear]=p;    /*   根结点入队  */
		level=rear ;    /*  根是第1层的最后一个节点  */
		while (front<rear)
	     	{  	p=Queue[++front]; 
	     		if(p.data==x)
	     			return depth;
	         	if (p->Lchild!=NULL)
	               Queue[++rear]=p->Lchild;    /*   左结点入队  */
	         	if (p->Rchild!=NULL)
	               Queue[++rear]=p->Rchild;    /*   左结点入队  */
	          	if (front==level)  
	             /*  正访问的是当前层的最后一个结点  */
	             {  depth++ ;  level=rear ;  }
	      }
	}
}

练习：求一棵树的最大宽度

//方法1 递归
int MaxWidth(BiTree T )
{
	if(T==NULL)
		return 0;
	else
	{
		int W[MaxSize]=0;
		int MaxW=0;
		Width(T,W,0);
		for(int i=0;W[i]!=0;i++)
			if(W[i]>MaxW)
				MaxW=W[i];
		return MaxW;
	}
}
void Width(BiTree T,int W[],int level)
{
	if(T)
	{
		W[level]++;
		Width(T->left,W,level+1);
		Width(T->right,W,level+1);
	}
}
//方法2 层次遍历
typedef struct{
	btnode *p;
	int layer;//层数
}st;
int find_max(btnode *b){
	st que[maxsize];//非循环队列
	int front=0,rear=0;
	int lno=0,i,j,n,max=0;
	btnode *q;
	if(b!=null){
		que[++rear].p=b;
		que[rear].layer=1;
		while(front!=rear){
			++front;
			q=que[front].p;
			lno=que[front].layer;
			if(q->lchild!=NULL){
				que[++rear].p=q->lchild;
				que[rear].layer=lno+1;
			}
			if(q->rchild!=NULL){
				que[++rear].p=q->rchild;
				que[rear].layer=lno+1;
			}
		}
	}
	for(i=1;i<=lno;++i){
		n=0;
		for(j=0;j<rear;j++){
			if(que[j].layer==i)++n;
			if(max<n)max=n;
		}
	}
	return max;
}

练习：求二叉树的所有路径

即返回所有从根节点到叶子结点的路径。

vector<string> path(node *root){
	vector<string> res;
	if(root==NULL)return res;
	dfs(root,to_string(root->val),res);//刚开始path只有root->val组成
	return res;
}
void dfs(node *root,string path,vector<string> &res){
	if(root->left==NULL &&root->right==NULL)
		res.push_back(path);
	if(root->left!=NULL)
		dfs(root->left,path+"->"+to_string(root->left->val),res);
	if(root->right!=NULL)
		dfs(root->right,path+"->"+to_string(root->right->val),res);
}
//第二个版本
int i,top=0;
char pathstack[maxsize];
void allpath(btnode *p){
	if(p!=NULL){
		pathstack[top]=p->data;
		top++;
		if(p->lchild==NULL&&p->rchild==NULL){
			for(i=0;i<top;++i)
				cout<<pathstack[i];
		}
		allpath(p->lchild);
		allpath(p->rchild);
		--top;
	}
}

练习：求给定节点至根节点的路径

考点栈的应用+后序遍历
有两种题目，意义相同

查找值为x的节点并输出该节点的所有祖先
从树的根结点开始往下访问一直到叶结点所经过的所有结点形成一条路径。打印出求出根结点到给定某结点之间的路径。

typedef struct{
	BiTree t;
	int tag;//tag=0左孩子被访问 tag=1右孩子被访问
}stack;
void search(BiTree bt int x){
	stack s[];
	top=0;
	while(bt!=NULL||top>0){
		while(bt!=NULL&&bt->data!=x){
			s[++top].t=bt;
			s[top].tag=0;
			bt=bt->lchild;
		}
		if(bt->data==x){
			for(i=1;i<=top;i++)
				cout<<s[i].t->data<<" ";
			return;
		}
		while(top!=0&&s[top].tag==1)top--;
		//左右孩子遍历过并且该节点均不为x直接退栈
		if(top!=0){
			s[top].tag=1;
			bt=s[top].t->rchild;
		}
	}
}

练习：求结点之间的距离/求两个节点的最近公共祖先

两种情况，一种经过根节点，另一种不经过根节点，只经过他们的共同祖先。
思路：找到a,b共同祖先，距离=a到共同祖先的距离+b到共同祖先的距离。
在这里插入图片描述

typedef struct{
	BiTree t;
	int tag;//tag=0左孩子被访问 tag=1右孩子被访问
}stack;//存放经过该节点的所有祖先

int search_parents(BiTree bt, char x,stack &s){
	top=0;
	while(bt!=NULL||top>0){
		while(bt!=NULL&&bt->data!=x){
			s[++top].t=bt;
			s[top].tag=0;
			bt=bt->lchild;
		}
		if(bt->data==x){
			//for(i=1;i<=top;i++)
				//cout<<s[i].t->data<<" ";
			return top;//路径中最大的可用下标是top
		}
		while(top!=0&&s[top].tag==1)top--;
		//左右孩子遍历过并且该节点均不为x直接退栈
		if(top!=0){
			s[top].tag=1;
			bt=s[top].t->rchild;
		}
	}
}

int max_path(char a,char b,BiTree bt){
	stack sa[101],sb[101];
	int n1=search_parents(bt,a,sa);
	int n2=search_parents(bt,b,sb);
	int deepest_parent=1;//离a,b节点最贴近的共同祖先
	for(int k=0;k<=min(n1,n2);k++){
		if(sa[k]!=sb[k])
			continue;
		else {
			if(deepest_parent<k) deepest_parent=k;
		}
	}
	int len_a=-1,len_b=-1;
	for(int k=deepest_parent;k<=n1;k++){
		if(sa[k]!=a)
			len_a++;
		else break;
	}
	for(int k=deepest_parent;k<=n2;k++){
		if(sb[k]!=b)
			len_b++;
		else break;
	}
	return len_a+len_b;
}

//求最近公共祖先 更简便的方法 递归
node* lowestcommon(node *root,node *p,node *q)//求p,q共同祖先
{
	if(!root||!q||!p){
		return NULL;
	}
	if(root==p||root==q)
		return root;
	node *l=lowestcommon(root->left,p,q);
	node *r=lowestcommon(root->right,p,q);
	if(l&&r)return root;
	return l?l:r;
}

练习：求左子树叶子结点和右子树叶子结点之间的最远距离

思路很简单，就是记录每个节点的左子树最长距离，右子树最长距离。最远距离为某个节点的左子树最大距离+右子树最大距离+2；2表示该节点左子树根节点到该节点的距离1加上该节点右子树根节点到该节点的距离1。

struct node{
	node *left;
	node *right;
	int data;
	int maxleft;
	int maxright;
}node;

int maxlen=0;
void findmaxlen(node *proot){
	if(proot==NULL)
		return;
	if(proot->left==NULL)
		proot->maxleft=0;
	else findmaxlen(proot->left);
	if(proot->right==NULL)
		proot->right=0;
	else findmaxlen(proot->right);
	
	if(proot->left!=NULL)
		proot->maxleft=(proot->left->maxleft>proot->left->maxright)?proot->left->maxleft:proot->left->maxright;
		proot->maxleft++;
}
	if(proot->right!=NULL)
		proot->maxright=(proot->right->maxleft>proot->right->maxright)?proot->right->maxleft:proot->right->maxright;
		proot->maxright++;
}

变形题目：求二叉树的直径即任意两个节点的最长路径

可能这条最长路径经过根节点，则最长路径为左子树深度+右子树深度
不经过根节点时，分成子问题，左子树右子树分别设为新的根，重复1.中过程
当然，n>2时这两个节点必为叶节点，n=2时一个是叶节点，一个是根节点。n不可能<2。

int depth(node *root){
	if(!root)return 0;
	return 1+max(depth(root->left),depth(root->right));
}
int maxlen(node *root){
	if(!root)return 0;
	int res=depth(root->left)+depth(root->right);
	return max(res,max(maxlen(root->left),maxlen(root->right)));
}

练习：判断是否是平衡二叉树/求树的高度

定义：左右子树高度差绝对值不大于1.

int height(node *root){
	if(root==NULL)return 0;
	return max(height(root->left),height(root->right))+1;
}
bool is_balanced(node *root){
	if(root==NULL)return true;
	return is_balanced(root->left)&&is_balanced(root->right)&&(abs(height(root->left)-height(root->right))<=1)
}

练习：计算树的带权路径长度

//采用先序遍历
int wpl(bitree *t){
	return preorder_wpl(t,0);
}
int preorder_wpl(bitree *p,int deep){
	int wpl_value=0;
	if(p->lchild==NULL&&p->rchild==NULL){
		wpl_value+=p->weight*deep;
	}
	if(p->lchild)preorder_wpl(p->lchild,deep+1);
	if(p->rchild)preorder_wpl(p->rchild,deep+1);
	return wpl_value;
}

练习：孩子兄弟链表存储结构的树求树的深度

算法思路：孩子兄弟链表表示的树求深度也是高度，
若是空树，为为0；否则高度为max（树的根节点到各个叶节点路径中利用左指针即*firstchild的个数+1）。

int height(cstree bt){
	int hc,hs;
	if(bt==NULL)return 0;
	else return max(1+height(bt->firstchild),height(bt->nextsibling));
}

练习：已知一棵树的层次序列和每个节点的度，构造该树的孩子兄弟链表

算法思路：跟层次序列有关，可设立辅助数组pointer[]按照树的层次序列存储各结点，根据节点的度链接各结点。

void create_cstree(cstree &t,char e[],int degree[],int n){
//层次序列e 节点个数n
	csnode *pointer=new csnod[maxnodes];
	int i,j,d,k=0;
	for(i=0;i<n;i++){
		pointer[i]->data=e[i];
		pointer[i]->lchild=pointer[i]->rsibling=NULL;
	}
	for(i=0;i<n;i++){
		d=degree[i];
		if(d){
			k++;pointer[i]->lchild=pointer[k];//i的第一个孩子结点分到lchild
			for(j=2;j<=d;j++){//剩余结点依次放入第一个孩子结点的兄弟节点
				k++;
				pointer[k-1]->rsibling=pointer[k];
			}
		}
	}
	t=pointer[0];
	delete [] pointer;
}

二叉树线索化

//前序线索化就是把链接线索代码提到了两递归入口前面
void pre_thread(tbtnode *p,tbtnode *&pre){
	if(p!=NULL){
		if(p->lchild==NULL){
			p->lchild=pre;
			p->ltag=1;
		}
		if(pre!=NULL&&pre->rchild==NULL){
			pre->rchild=p;
			pre-rtag=1;
		}
		pre=p;
		if(p->ltag==0)
			pre_thread(p->lchild,pre);
		if(p->rtag==0)
			pre_thread(p->rchild,pre);
	}
}
//前序线索二叉树上执行前序遍历
void preorder(tbtnode *root){
	if(root!=NULL){
		tbtnode *p=root;
		while(p!=NULL){
			while(p->ltag==0){
				visit(p);
				p=p->lchild;
			}
			visit(p);//此时p左指针必为线索，则p的左孩子不存在
			p=p->rchild;//指向其后继
		}
	}
}
//先序线索化非递归版
void preorder_Threading(BiThrNode *T)
 {  BiThrNode  *stack[MAX_NODE];
	BiThrNode  *last=NULL, *p ;
	int top=0 ;
	if  (T!=NULL)
	{  stack[++top]=T;
		while (top>0)
    	{   p=stack[top--] ;
        	if (p->Lchild!=NULL)  p->Ltag=0 ;
        	else  {  p->Ltag=1 ;  p->Lchild==last ;  }
        	if  (last!=NULL)
            	if (last->Rchild!=NULL) last->Rtag=0 ;
            	else{ last->Rtag=1 ; last->Rchild==p ;  }
            last=p ;
        	if (p->Rchild!=NULL) 
            	stack[++top]=p->Rchild ; 
        	if (p->Lchild!=NULL)
             	stack[++top]=p->Lchild ;
   		}
		Last->Rtag=1;  /*   最后一个结点是叶子结点 */
	}
}
//中序线索化非递归版
void inorder_Threading(BiThrNode *T)
 {  BiThrNode  *stack[MAX_NODE];
	BiThrNode  *last=NULL, *p=T ;
	int top=0 ;
	while  (p!=NULL||top>0){
		if  (p!=NULL)  {  stack[++top]=p;  p=p->Lchild;  }
		else
		{   p=stack[top--] ;
   		    if (p->Lchild!=NULL)  p->Ltag=0 ;
    		else  {  p->Ltag=1 ;  p->Lchild==last ;  }
    		if  (last!=NULL){
        	if (last->Rchild!=NULL) last->Rtag=0 ;
        	else {  last->Rtag=1 ; last->Rchild==p ;  }
        }
    	last=p ; 
   		P=p->Rchild; 
	}
	last->Rtag=1;  /*   最后一个结点是叶子结点   */}
}
//中序遍历建立中序线索二叉树
void in_thread(tbtnode *p,tbtnode *&pre){
	if(p!=NULL){
		in_thread(p->lchild,pre);
		if(p->lchild==NULL){
			p->lchild=pre;
			p->ltag=1;
		}
		if(pre!=NULL&&pre->rchild==NULL){
			pre->rchild=p;
			pre-rtag=1;
		}
		pre=p;
		in_thread(p->rchild,pre);
	}
}
void create_inthread(tbtnode *root){
	tbtnode *pre=NULL;
	if(root!=NULL){
		in_thread(root,pre);
		pre->rchild=NULL;
		pre->rtag=1;
	}
}
//中序线索二叉树的遍历
tbtnode *first(tbtnode *p)//求中序线索二叉树中的第一个节点
{
	while(p->ltag==0)
		p=p->lchild;
	return p;
}
tbtnode *next(tbtnode *p)//求中序线索二叉树中的节点p的后继节点
{
	if(p->rtag==0)
		return first(p->rchild);
	else return p->rchild;
}
tbtnode *last(tbtnode *p)//求中序线索二叉树中的最后一个节点
{
	while(p->rtag==0)
		p=p->rchild;
	return p;
}
tbtnode *prior(tbtnode *p)//求中序线索二叉树中的节点p的前驱节点
{
	if(p&&p->ltag==0)
		return last(p->lchild);
	else return p->lchild;
}

tbtnode *pre_next(tbtnode *p)//求中序线索二叉树中节点p前序下的后继
{
/* a有左子女时选左子树根节点为后继，无左子女有右子女时选右子女根节点，
无左子女也无右子女，沿后继指针找到终点c，取c的右子女
*/
	if(p&&p->ltag==0)
		return p->lchild;
	else if(p->rtag==0)
		return p->rchild;
	else{
		tbtnode *t=p;
		while(t&&t->rtag)
			t=t->rchild;
		if(t)t=t->rchild;
		return t;
	}
}

//遍历中序线索二叉树 即在该树上执行中序遍历
void inorder(tbtnode *root){
	for(tbtnode *p=first(root);p!=NULL;p=next(p)
		visit(p);
}

//后序线索二叉树
//链接线索代码放到了两递归入口的后面
void post_thread(tbtnode *p,tbtnode *&pre){
	if(p!=NULL){
		post_thread(p->lchild,pre);
		post_thread(p->rchild,pre);
		if(p->lchild==NULL){
			p->lchild=pre;
			p->ltag=1;
		}
		if(pre!=NULL&&pre->rchild==NULL){
			pre->rchild=p;
			pre-rtag=1;
		}
		pre=p;
	}
}

依照线性表结构，也在二叉树线索链表中添加一个头节点，令头节点lchild指向二叉树根节点，rchild指向中序遍历访问的最后一个节点；二叉树中序序列第一个节点的lchild和最后一个节点的rchild均指向头节点。建立双向线索链表，对一棵线索二叉树既可从头结点也可从最后一个结点开始按寻找直接后继进行遍历。

//以双向线索链表作为存储结构对二叉树进行遍历
status inorder_traverse(biThrTree t){
	p=t->lchild;
	while(p!=t){
		while(p->ltag==0)p=p->lchild;
		visit(p);
		while(p->rtag==1&&p->rchild!=t){
			p=p->rchild;visit(p);
		}
		p=p->rchild;
	}
}
status inorder_threading(biThrTree &thrt biThrTree t){
	if(!(thrt=(biThrTree)malloc(sizeof(biThrNode)))exit(overflow);
	thrt->ltag=0;thrt->rtag=1;
	thrt->rchild=thrt;
	if(t==NULL)thrt->lchild=thrt;
	else{
		thrt->lchild=t;
		pre=thrt;
		in_threading(t);
		pre->rchild=thrt;
		pre->rtag=1;
		thrt->rchild=pre;
	}
	return ok;
}
void in_threading(biThrTree p){
	if(p){
		in_threading(p->lchild);
		if(!p->lchild){p->ltag=1;p->lchild=pre;}
		if(!pre->rchild){pre->rtag=1;pre->rchild=p;}
		pre=p;
		inthreading(p->rchild);
	}
}

练习：中序线索二叉树中给出某节点的后序遍历前驱

算法思路：首先在后序序列中分类讨论各种可能情况

若该节点p有右子女，则其右子女是其后序前驱；若无右子女而有左子女，左子女是其后序前驱。
左右子女都没有时，走到其中序前驱线索节点处（也就是p的父节点f）
若f有左子女，则该左子女是p后序前驱；若没有左子女，则顺前驱找f的双亲（若存在的话）直到找到有左子女的双亲返回这个左子女；否则其后序前驱为null

bithrt inpostpre(bithrt t,tithrt p){//t是中序线索二叉树 p是指定节点
	bithrt q;
	if(p->rtag==0)q=p->rchild;
	else if(p->ltag==0)q=p->lchild;
	else if(p->lchild==NULL)q=NULL;
	else{
		while(p->ltag==1&&p->lchild!=NULL)
			p=p->lchild;
		if(p->ltag==0)q=p->lchild;
		else q=NULL;
	}
	return q;
}

建立二叉排序树

递归和非递归版

//递归
void creatBSortTree2(PNode &t,int data){
	if(t==NULL){
		PNode p=(PNode)malloc(sizeof(Node));
		p->data=data;
		p->lchild=NULL;
		p->rchild=NULL;
		t=p;
		return;
	}else if(t->data>data)
		creatBSortTree2(t->lchild,data);
	else creatBSortTree2(t->rchild,data);
}
//非递归
void creatBSortTree(PNode &t,int data){
	PNode p=(PNode)malloc(sizeof(Node));
	p->data=data;
	p->lchild=NULL;
	p->rchild=NULL;
	if(t==NULL){
		t=p;
		return;
	}
	PNode q=t,parent;
	while(q!=NULL){
		parent=q;
		if(parent->data>data)
			q=parent->lchild;
		else
			q=parent->rchild;
	}
	if(parent->data>data)
		parent->lchild=p;
	else parent->rchild=p;
}

在二叉排序树里查找key

BTNode* BSTSearch(BTNode* p,int key){
	while(p!=NULL){
		if(key==p->key)
			return p;
		else if(key<p->key)
			p=p->lchild;
		else p=p->rchild;
	}
	return NULL;
}

检验是否是二叉排序树

误区：不能递归的通过根节点大于左节点小于右节点来判断。
思路：要通过中序遍历得到不递减的序列来判断。

int pre=-10000;//始终记录当前所访问节点的前驱的值
int judge_bst(BTNode *bt){
	int b1,b2;
	if(bt==NULL)return 1;
	else{
		b1=judge_bst(bt->lchild);//放在这 pre指的是左子树节点
		if(b1==0||pre>bt->data)
		//中序遍历只需要后面出现的序列比前面出现的序列大即可
			return 0;
		pre=bt->data;
		b2=judge_bst(bt->rchild);//放在这 pre指的是其根节点
		return b2;
	}
}

二叉排序树节点中含有关键字key域和统计相同关键字值节点个数的count域，当向该树插入一个元素时，若树中存在该节点则其count++，否则生成一个新节点插入树中，并置count=1

void insert(BTNode *&t,BTNode *&pr,int x){
	BTNode *p=t;
	while(p!=NULL){
		if(p->data!=x){
			pr=p;
			if(x<p->data)
				p=p->lchild;
			else p=p->rchild;
		}else{
			++(p->count);
			return;
		}
	}
	BTNode *s=(BTNode*)malloc(sizeof(BTNode));
	s->data=x;
	s->count=1;
	s->lchild=s->rchild=NULL;
	if(pr==NULL)t=s;
	else if(x<pr->data)pr->lchild=s;
	else pr->rchild=s;
}

判断给定的关键字值序列（关键字互不相同）是否是二叉排序树的查找序列，如果是返回1，否则返回0；

思路：假设寻找值等于x的节点，从给出的序列中依次生成两个子序列，s1包含小于等于x的数据，s2包含大于x的数据。如果s1单调递增，s2单调递减，则是一个查找序列。
但目前并未给定x，只有需要判断的查找序列，只能得到s1,s2子序列，即依次比对两个元素，e[i]<e[i+1]时放入s1，>放入s2。指定一个x后，检测s1是否单调递增且均小于等于x，检测s2是否单调递减且大于x即可

typedef struct{
	int elem[maxsize];
	int len;
}sequence;
void reduce(sequence &s,sequence &s1,sequence &s2){
	int i=0,j=0,k=0;
	while(i+1<len){
		while(i+1<s.len&&s.elem[i]<s.elem[i+1])
			s1.elem[j++]=s.elem[i++];
		while(i+1<s.len&&s.elem[i]>s.elem[i+1])
			s2.elem[k++]=s.elem[i++];
	}
	s1.len=j;s2.len=k;
}
int judge(sequence &s1,sequence &s2,int x){
	int i,flag;
	flag=1;
	i=0;
	while(flag&&i+1<s1.len){
		if(s1.elem[i]>s1.elem[i+1]||s1.elem[i]>x)
			flag=0;
		else i++;
	}
	i=0;
	while(flag&&i+1<s2.len){
		if(s2.elem[i]<s2.elem[i+1]||s2.elem[i]<x)
			flag=0;
		else i++;
	}
	return flag;
}
int issearch(sequence &s,sequence &s1,sequence &s2,int x){
	reduce(s,s1,s2);
	return judge(s1,s2,x);
}

在平衡二叉树的每个节点增设域size，存储以该节点为根的左子树的节点个数+1，确定树中第k个(k>=1)节点的位置

BTNode *search(BTNode *t,int k){
	if(t==NULL||k<1)
		return NULL;
	if(t->lsize==k)return t;
	if(t->lsize>k)return search(t->lchild,k);
	else return search(t->rchild,k-t->size);
}

图

//nextneighbor函数
//邻接矩阵版
int nextneighbor(mgraph &g,int x,int y){
	if(x!=-1&&y!=-1){
		for(int col=y+1;col<g.vexnum;col++)
			if(g.edge[x][col]>0&&g.edge[x][col]<maxweight)return col;
	}
	return -1;
}
//邻接表版
int nextneighbor(algraph &g,int x,int y){
	if(x!=-1){
		arcnode *p=g.vertices[x].first;
		while(p!=NULL&&p->data!=y)p=p->next;
		if(p!=NULL&&p->next!=NULL)return p->next->data;
	}
	return -1;
}

邻接矩阵

存储两点之间是否有边/距离值
无向图邻接表的特点：沿主对角线对称，主对角线上为0。

for(i=1;i<n;i++)
	for(j=1;j<n;j++)
		if(i==j)e[i][j]=0;
		else e[i][j]=99999999;//inf
//读入图中的边
for(i=1;i<m;i++)
{
	scanf("%d %d",&a,&b);
	e[a][b]=1;
	e[b][a]=1;//有向图要把这条代码删掉，不具备对称性
}
//dfs 根据邻接矩阵遍历图
book[1]=1;
dfs(1);

void dfs(int cur)//当前顶点编号
{
	printf("%d",cur);
	sum++;//记录访问的节点个数
	if(sum==n)return;
	for(i=1;i<=n;i++)
	{
		if(e[cur][i]==1&&book[i]==0)//cur到i有边且定点i未被探索过
		{
			book[i]=1;dfs(i);
		}
	}
	return;
}

//bfs 根据邻接矩阵遍历图
int head=1,tail=1;
que[tail++]=1;//迷宫入口
book[1]=1;
	
	while(head<tail&&tail<=n){
		cur=que[head];
		for(i=1;i<=n;i++)//1~n依次尝试
		{
			if(e[cur][i]==1&&book[i]==0){
				book[i]=1;
				que[tail++]=i;
			}
			if(tail>n)break;
		}
		head++;//非常重要 忘记则导致搜索无法拓展

邻接表

练习：统计入度

//统计各顶点入度的函数
void count_indegree(ALGraph *G)
{  int k ; LinkNode *p ;
	for (k=0; k<G->vexnum; k++)
		G->adjlist[k].indegree=0 ;     /*  顶点入度初始化  */
	for (k=0; k<G->vexnum; k++)
	{  	p=G->adjlist[k].firstarc ;
		while (p!=NULL)     /*  顶点入度统计  */
	    {   G->adjlist[p->adjvex].indegree++ ;
	        p=p->nextarc ;   
	    }
	}
}

十字链表

最短路径

dfs,bfs,floyd,dijkstra等方法。

int min=99999999;
int inf=99999999;
void dfs(int cur,int dis)//当前顶点编号 距离distance
{
	if(dis>min)return;
	if(cur==n){
		if(dis<min)min=dis;//更新min
		return;
	}
	for(i=1;i<=n;i++)
	{
		if(e[cur][i]!=inf&&book[i]==0)//cur到i有边且定点i未被探索过
		{
			book[i]=1;
			dfs(i,dis+e[cur][i]);
			book[i]=0;//撤回操作
		}
	}
	return;
}

floyd-多源最短路径

思想：动态规划的思想。从最开始的只允许经过顶点1进行中转（如果在新增的这点中转能得到更小的距离则采用），到之后只允许经过顶点1和2，.，最后到允许经过顶点1～n进行中转，最终得到任意两点之间最终的最短路径。可以处理带负权边的图，但不能含有负权回路（环）。

//核心代码只有5行
for(k=1;k<=n;k++)
	for(i=1;i<=n;i++)
		for(j=1;j<=n;j++)//时间复杂度显然为o(n^3)
			if(e[i][j]>e[i][k]+e[k][j])
				e[i][j]=e[i][k]+e[k][j];
//为防止溢出超出int范围，可以改进代码
for(k=1;k<=n;k++)
	for(i=1;i<=n;i++)
		for(j=1;j<=n;j++)
			if(e[i][k]<inf&&e[k][j]<inf&&e[i][j]>e[i][k]+e[k][j])
				e[i][j]=e[i][k]+e[k][j];

dijkstra- 单源最短路径

基于贪心算法，图中不能有负权边。一轮下来只能得到某个点到其余各点的最短路径。总结为：

将所有顶点分成两个子集，已知最短路径的节点集p（用book数组标记），和未知最短路径的节点集q。
每次找到q中离源点最近的一个顶点，将其转移到p集，以该顶点作为中心扩展试图松弛每条以该顶点为起点的边。
最终找到源点到其余所有点的最短路径，即q集为空算法结束。
如果使用堆排序寻找最近顶点可将整个算法时间复杂度降到o((n+m)logn)
松弛操作是dijkstra算法主要思想，即dis[j]>dis[j-1]+e[j-1][j]则dis[j]=dis[j-1]+e[j-1][j]；

//核心代码
//book数组初始化略
for(i=1;i<=n;i++){
	dis[i]=e[1][i];//找离1号顶点到各顶点的最短路径
}
//用邻接表代替邻接矩阵可将复杂度从o(n^2)->o((m+n)logn)
for(i=1;i<n;i++){//时间复杂度为o(n^2)
	min=inf;
	for(j=1;j<=n;j++)
	{
		if(book[j]==0&&dis[j]<min){//找当前阶段的最小dis点放入q集
		//这部分用堆排序可将单个时间复杂度从o(n)->o(logn)
			min=dis[j];
			u=j;
		}
	}
	book[u]=1;
	for(v=1;v<=n;v++){{
		if(e[u][v]<inf){
			if(dis[v]>dis[u]+e[u][v])
				dis[v]=dis[u]+e[u][v];//更新min(dis)
		}
	}
}
//完整代码
int  set[MAX_VEX],path[MAX_VEX],dist[MAX_VEX] ;
void Dijkstra (mgraph *g, int v) /*   从图G中的顶点v出发到其余各顶点的最短路径  */
{   int i,j,u, min ; 
	for ( j=0; j<g.n; j++)
	{   
		set[j]=0 ;
		dist[j]=g.edges[v][j] ;
		if(g.edges[v][i]<inf)
			path[j]=v ;  
		else path[j]=-1;
	} 
	path[v]=-1 ; 
	set[v]=1; 
	for ( j=0; j<g.n-1; j++) /*  其余n-1个顶点  */
	{  	min=inf ; 
		for ( k=0; k<g.n; k++)
	    {  if(set[k]==0&&dist[k]<min)
	       {   	min=dist[k] ;  
	       	   	u=k ; 
	       }
	   	}     /* 求出当前最小的dist[k]值  */
		set[u]=1 ;      /*  将第k个顶点并入S中  */
		for ( j=0; j<g.n; j++)
	    {  if(set[j]==0&&(dist[u]+g.edges[u][j]<dist[j]))
	       {   dist[j]=dist[u]+g.edges[u][j] ; 
	           path[j]=u ;  
	       }
	    }            
	}      
}

//用数组实现邻接表
int n,m//n顶点数，m边数
int u[m+1],v[m+1],w[m+1];
//表示第i条边从第u[i]号节点到第v[i]号节点，权值为w[i]
int first[n+1],next[m+1];
//first[u[i]]保存顶点u[i]的第一条边的编号 first[]=-1时表示该点没有出边
//next[i]保存“编号为i的边的下一条边”
/*
也就是说next[first[i]]为u[i]节点第一条边的下一条边的编号，也是u[i]为起点的第二条边的编号
next[next[first[i]]]是接下来u[i]为起点的第三条边的编号
当编号为-1时表示之后没有该顶点的下一条边
*/

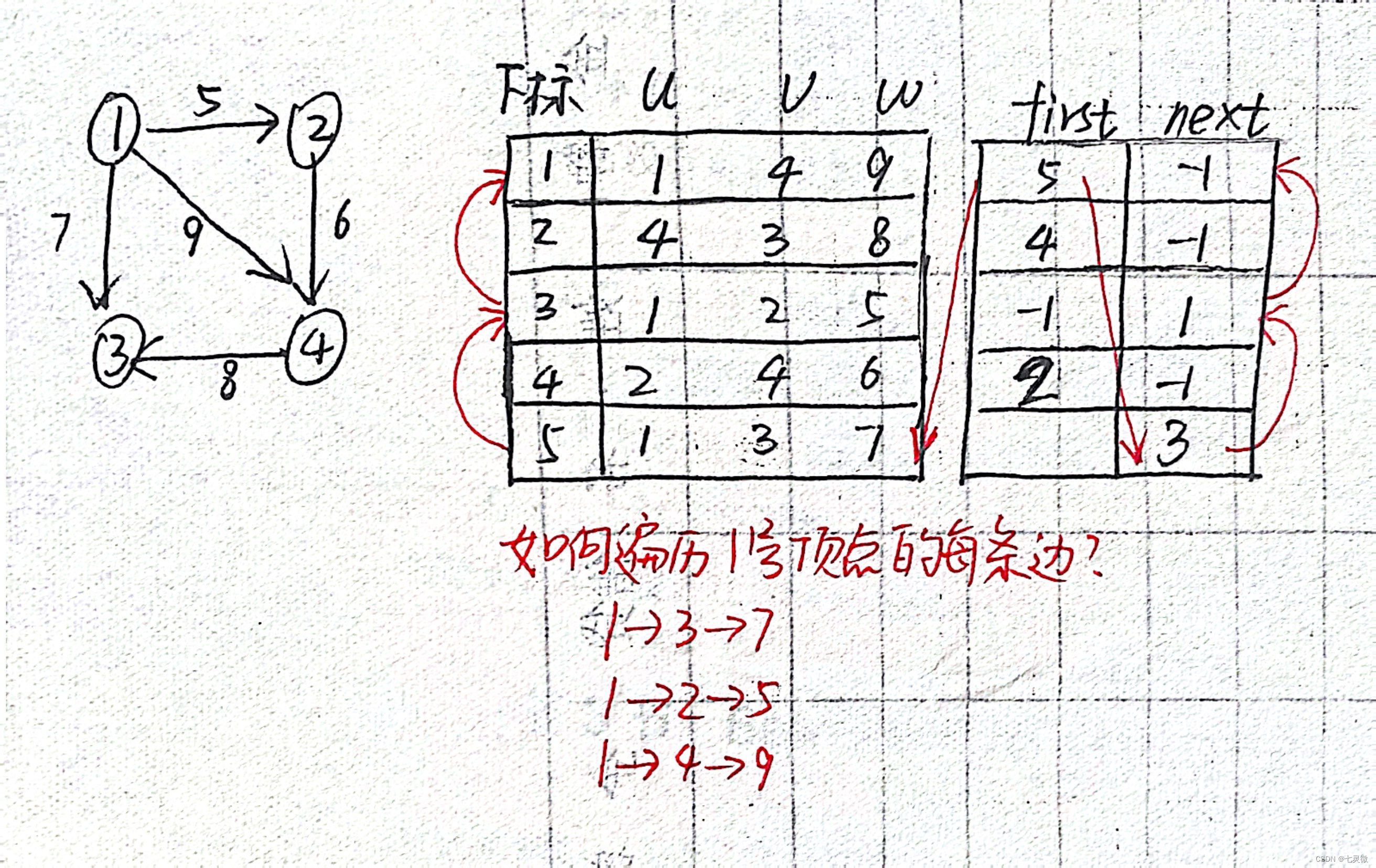
在这里插入图片描述
用邻接表遍历图时间复杂度是o(m边长)，如果是稀疏图的话应选用邻接表存储，省时间和空间复杂度。

几大算法对比

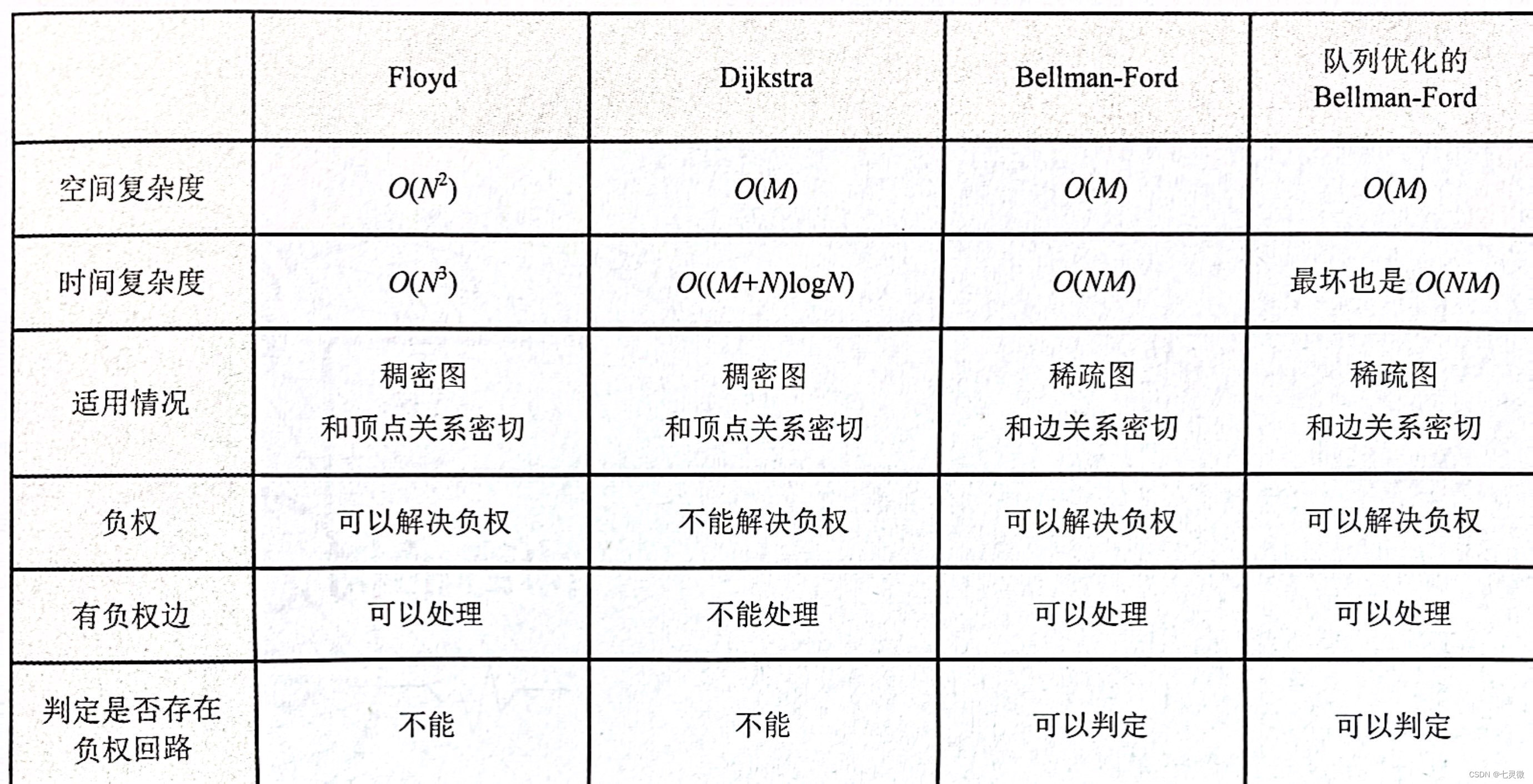
在这里插入图片描述
dijkstra通过堆优化时间复杂度可到o(mlogn)

最小生成树

最少的边使得图连通，如果有n个节点则至少需要n-1条边。
如果所有边权值互不相等则最小生成树唯一
kruskal算法是一步步将森林的树合并，更适合稀疏图；prim是每次增加一条边建立一棵树，更适合稠密图，用堆优化的prim之后更适用于稀疏图。

kruskal算法：按从小到大边权值排序，先选最小的且两个顶点不在同一个集合的边（防止产生回路），取n-1条使得图连通。算法中难实现的是如何判断图连通？dfs,bfs固然可以但是效率低，选择并查集，判断两个顶点是否连通是需要看他们是否在同一集合，时间复杂度仅o(logn)；
总体算法时间复杂度为o(mlogm+mlogn)，对边快排o(mlogm)，在m条边中找出n-1条边o(mlogn)，通常m>>n，最终得到o(mlogm)
prim算法：将所有顶点分成两类，（已加入生成树的顶点）树顶点和非树顶点，选出一条边添加到生成树，这需要枚举每一个树顶点到非树顶点所有的边，（可以优化找到下一个添加到生成树的边，思想类似与dijkstra，记录生成树到各顶点的距离）并且找到其中最短的加入到生成树。重复n-1次直到所有顶点都加入到生成树。
整个算法时间复杂度是o(n^2)；
若借助堆每次选边时间复杂度为o(logm)再用邻接表存储图，则整个算法时间复杂度降低到o(mlogn)；
如何借助堆？利用数组h建立一个堆，堆里存放顶点编号，按照顶点在数组dis中的值来排序，用pos数组记录每个顶点在最小堆中的位置。

算法流程如下
1. 从任意顶点开始构造生成树，比如加入顶点1，并且用book数组标记是否加入生成树
2. 用数组dis记录当前生成树到各个节点最短距离，最初生成树只有顶点1，故dis存储的就是顶点1到各顶点边的权值
3. 从数组dis中选出离生成树最近的点j加入生成树，再以j为中间点，更新生成树到每个非树顶点的距离，if (dis[k]>e[j][k] )dis[k]=e[j][k];
4. 重复直至生成树中有n个顶点。

//tianqin浓缩版 感觉这个版本更方便理解记忆
//lowcost记录当前生成树到各个节点最短距离,vset[i]=1表示i点已加入最小生成树
void prim(mgragh g,int v0,int &sum){
	int lowcost[maxsize],vset[maxsize],v;
	int i,j,k,min;
	v=v0;
	for(i=0;i<g.n;i++){
		lowcost[i]=g.edges[v0][i];
		vset[i]=0;
	}
	vset[v0]=1;
	sum=0;
	for(i=0;i<g.n-1;++i)//重复n-1次，选出n-1条边
	{
		min=inf;
		for(j=0;j<g.n;++j)//选出最小候选边
			if(vset[j]==0&&lowcost[j]<min){
				min=lowcost[j];
				k=j;
			}
		vset[k]=1;
		v=k;
		sum+=min;
		for(j=0;j<g.n;j++)
			if(vset[j]==0&&g.edges[v][j]<lowcost[j])
				lowcost[j]=g.edges[v][j];
	}
}
//kruskal tianqin浓缩版
typedef struct{
	int a,b;//边的两个顶点
	int w;//边权值
}road;//图信息存储在其中
road r[maxsize];
int v[maxsize];//并查集数组
int getroot(int a){
	while(a!=v[a])a=v[a];
	return a;
}
void kruskal(mgraph g,int &sum,road r[]){//sum生成树的权值
	int i;
	int n=g.n,e=g.e,a,b;
	sum=0;
	for(i=0;i<n;i++)v[i]=i;//并查集初始化
	sort(road,e);//对e条边进行排序
	for(i=0;i<e;i++){
		a=getroot(road[i].a);
		b=getroot(road[i].b);
		if(a!=b){
			v[a]=b;
			sum+=road[i].w;
		}
	}
}

//kruskal
struct edge
{
    int u;
    int v;
    int w;
}e[10];
int n,m;
int f[7]={0},sum=0,counter=0;
void quicksort(int left,int right)
{
    int i,j;
    struct edge t;
    if(left > right)
        return;
 
    i = left;
    j = right;
    while(i!=j)
    {
        //注意顺序
        //先从右边找
        while(e[j].w >= e[left].w && i < j)
            j--;
        //从左边找
        while(e[i].w <= e[left].w && i < j)
            i++;
        if(i<j)
        {
            t = e[i];
            e[i]= e[j];
            e[j] = t;
            //swap(e[i],e[j]);
        }
    }
    //基准归位
    t = e[left];
    e[left]= e[i];
    e[i] = t;
    //swap(e[left],e[i]);
    quicksort(left, i-1);
    quicksort(i+1, right);
    return;
}
 
int getf(int v)
{
    if(f[v]==v)
        return v;
    else
    {
        //路径压缩，找到每个人的祖宗
        f[v] = getf(f[v]);
        return f[v];
    }
}
 
bool merge(int v,int u)//合并两个子集合
{
    int t1,t2;//t1,t2分别为v和u的boss，每次都是用boss解决
    t1=getf(v);
    t2=getf(u);
    if(t1!=t2)
    {
        f[t2] = t1;//靠左原则
        return 1;
        //路径压缩后，将f[u]的根值夜赋值为v的祖先f[t1]
    }
    return 0;
}
int main()
{
    scanf("%d%d",&n,&m);
 
    for(int i=1;i<=m;i++)
        scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].w);
 
    quicksort(1,m);//边权值排序
 
    //并查集初始化
    for(int i=1;i<=n;i++)
        f[i]=i;
 
    //Kruskal算法核心部分
    for(int i=1;i<=m;i++)//枚举从小到大的每条边
    {
        //判断一条边的两个顶点是否连通，即是否在一个集合中
        if(merge(e[i].u,e[i].v))
        {
            counter++;
            sum+=e[i].w;
        }
        if(counter == n-1)
            break;
    }
    printf("%d\n",sum);
    return 0;
}
//prim
const int INF = 99999999;
int e[7][7],dis[7],book[7]={0};
int main()
{
    int n,m;
    int counter = 0,sum = 0;
    scanf("%d%d",&n,&m);
 
    //初始化
    for(int i = 1;i <= n;i++)
        for(int j = 1;j <= n;j++)
            if(i == j)  e[i][j] = 0;
                else    e[i][j] = INF;
 
        int t1,t2,t3;
        for(int i = 1;i <= m;i++)
        {
            scanf("%d%d%d",&t1,&t2,&t3);
            e[t1][t2] = e[t2][t1] = t3;//无向图
        }
 
        //初始化dis数组
        for(int i = 1;i <= n;i++)
            dis[i] = e[1][i];
 
        //Prim算法核心
        //将1号顶点加入生成树
        book[1] = 1;
        counter++;
        int u,v,minn;
        while(counter < n)
        {
            minn = INF;
            for(int i = 1;i <= n;i++)
            {
                if(!book[i] && dis[i] < minn)
                {
                    minn = dis[i];
                    u = i;
                }
            }
 
            book[u] = 1;
            counter++;
            sum += dis[u];
            for(int v = 1;v <= n;v++)
            {
                if(!book[v] && dis[v] > e[u][v])
                   dis[v] = e[u][v];
            }
        }
        printf("%d\n",sum);
        return 0;
}
//prim 堆优化版
const int INF = 99999999;
const int N = 100;
int dis[N],book[N]={0};
int h[N],pos[N],size;
 
void swap(int x,int y)
{
    int t;
    t = h[x];
    h[x] = h[y];
    h[y] = t;
 
    t = pos[h[x]];
    pos[h[x]] = pos[h[y]];
    pos[h[y]] = t;
}
 
void siftdown(int i)
{
    int t,flag = 0;
    while(i*2 <= size &&flag == 0)
    {
        if(dis[h[i]] > dis[h[i*2]])
            t=2*i;
        else
            t = i;
 
        //如果它有左儿子，再对右儿子进行讨论
        if(i*2+1 <= size)
        {
            if(dis[h[t]] > dis[h[i*2+1]])
                t = i*2+1;
        }
        //如果发现最小的节点编号不是自己，说明子节点中有更小的
        if(t!=i)
        {
            swap(t,i);
            i = t;
        }
        else
            flag = 1;
    }
}
 
void siftup(int i)
{
    int flag = 0;
    if(i == 1)
        return;
    while(i!=1 && flag == 0)
    {
        if(dis[h[i]] < dis[h[i/2]])
            swap(i,i/2);
        else
            flag = 1;
        i/=2;
    }
}
 
int pop()
{
    int t;
    t = h[1];
    pos[t] = 0;
    h[1] = h[size];
    pos[h[1]] = 1;
    size--;
    siftdown(1);
    return t;
}
int main()
{
    int n,m,k;
    int u[N],v[N],w[N],first[N],next[N];
    int counter = 0,sum = 0;
    scanf("%d%d",&n,&m);
 
    //读入边
    for(int i = 1;i <= m;i++)
        scanf("%d%d%d",&u[i],&v[i],&w[i]);
 
        //无向图
        for(int i = m+1;i <= 2*m;i++)
        {
            u[i] = v[i-m];
            v[i] = u[i-m];
            w[i] = w[i -m];
        }
 
        //建立邻接表储存边
        for(int i = 1;i <= m;i++)
            first[i] = -1;
        for(int i = 1;i <= 2*m;i++)
        {
            next[i] = first[u[i]];
            first[u[i]] = i;
        }
 
        //Prim算法核心
        //讲1号顶点加入生成树
        counter++;
        book[1] = 1;
 
        //初始化dis数组，这里是1号顶点到其余各顶点的初始距离
        dis[1] = 0;
        for(int i = 2;i <= n;i++)
            dis[i] = INF;
            k = first[1];
            while(k != -1)
            {
                dis[v[k]] = w[k];
                k = next[k];
            }
 
            //初始化堆
            size = n;
            for(int i = 1;i <= size;i++)
            {
                h[i] = i;
                pos[i] = i;
            }
            for(int i = size/2;i >= 1;i--)
            {
                siftdown(i);
            }
            pop();//先弹出一个堆顶的元素，因为此时堆顶是1号顶点
            int j;
            while(counter < n)
            {
                j = pop();
                book[j] = 1;
                counter++;
                sum += dis[j];
 
                //扫描当前顶点j所有的边，再以j为中间节点，进行松弛
                k = first[j];
                while(k != -1)
                {
                    if(book[v[k]]==0&&dis[v[k]] > w[k])
                    {
                        dis[v[k]] = w[k];
                        siftup(pos[v[k]]);//对该点再堆中进行向上调整
                    }
                    k = next[k];
                }
            }
            printf("%d\n",sum);
}

遍历图

深度优先搜索（含栈）

递归中的系统栈，程序调用的栈也是一种栈。
基本模型
void dfs(int step){
判断边界
尝试每种可能for( i->n i++){
继续下一步def(step+1);
//可能包含撤回操作 book[i]=1;def(step+1);book[I]=0;例如全排列
//可能不需要撤回操作比如计算区域面积、挨个尝试地图上的点
}
返回
}

//两种 其实思路一样，哪个简单可以记哪个
void dfs(agraph *g,int v){
	arcnode *p;
	visit[v]=1;
	visit(v);
	p=g->adjlist[v].firstarc;
	while(p!=NULL){
		if(visit[p->adjvex]==0)
			dfs(g,p->adjvex);
		p=p->nextarc;
	}
}
//非连通图的遍历加上一个顶层循环
void dfs_main(agraph *g){
	int i;
	for(i=0;i<g->n;i++)
		if(visit[i]==0)
			dfs(g,i);
}
//非递归简单版
void dfs(AGraph *g,int v){
	ArcNode *p;
	int stack[maxsize],top=-1;
	int i,k;
	int visit[maxsize];
	for(i=0;i<g->n;i++)
		visit[i]=0;
	visit(v);
	visit[v]=1;
	stack[++top]=v;
	while(top!=-1){
		k=stack[top];
		p=g->adjlist[k].firstarc;
		while(p!=NULL&&visit[p->adjvex]==1)
			p=p->nextarc;
		if(p==NULL)--top;//不要着急退栈，等该节点完全利用完之后再退栈
		else{
			visit(p->adjvex);
			visit[p->adjvex]=1;
			stack[++top]=p->adjvex;
		}
	}
}
//dfs遍历图
#include<stdlib.h>
#include<stdio.h>
#define VexNum 100
int vex_loop;
vector<int> loop;
typedef struct Graph			//利用邻接矩阵表示
{
	char vexs[VexNum];			//顶点
	int arcs[VexNum][VexNum];	//边	
	int vexnum, arcnum;			//顶点和边的数量
}Graph;

int LocateVex(Graph *G, char c)	//输入顶点符号，寻找其对应的位置
{
	for (int i = 0; i < G->vexnum; i++)
	{
		if (G->vexs[i] == c)
			return i;
	}
}

void initGraph(Graph *G)					//图的初始化
{
	int i, j;
	char c1, c2;

	scanf("%d %d", &G->vexnum, &G->arcnum);
	getchar();

	for (i = 0; i < G->vexnum; i++)
	for (j = 0; j < G->vexnum; j++)
		G->arcs[i][j] = 0;				//初始化每条边为0

	for (i = 0; i < G->vexnum; i++)
		scanf("%c", &G->vexs[i]);			//输入点的信息

	for (int k = 0; k < G->arcnum; k++)			//创建边的信息
	{
		getchar();
		scanf("%c%c", &c1, &c2);			//输入一条边依附的顶点
		i = LocateVex(G, c1);				//找到顶点i的下标
		j = LocateVex(G, c2);				//找到顶点j的下标

		G->arcs[i][j] = G->arcs[j][i] = 1;
	}
}

bool visited[VexNum];

void DFS(Graph *G,char c0)					//从c0开始遍历整个图
{ 
	int index0, i;
	char e;

	index0 = LocateVex(G, c0);
	visited[index0] = 1;
	printf("%c ", c0);

	for (i = 0; i < G->vexnum; i++)
	{
		if (G->arcs[index0][i] )
		{
			if(!visited[i])//以下一个邻接点为顶点开始搜索
			{	e = G->vexs[i];
				DFS(G, e);	
			}		
		}
		
	}
}

void main(){
	Graph G;
	initGraph(&G);
	for (int i = 0; i < G.vexnum; i++){
		visited[i] = 0;
	}
	DFS(&G,'a');
}

练习：判断顶点i和j之间是否有路径 i不等于j

对顶点i进行一次dfs，若visit[j]==1则有路径

int dfs_main(agraph *g,int i,int j){
	int k;
	for(k=0;i<g->n;i++)
		visit[k]=0;
	dfs(g,i);
	if(visit[j]==1)
		return 1;
	else return 0;
}
//bfs方法
int bfs(agraph *g,int vi,int vj){
	Arcnode *p;
	int que[maxsize],front=0,rear=0;
	int visit[maxsize];
	int i,j;
	for(i=0;i<g.n;i++)
		visit[i]=0;
	rear=(rear+1)%maxsize;
	que[rear]=vi;
	visit[vi]=1;
	while(front!=rear){
		front=(front+1)%maxsize;
		j=que[front];
		if(j==vj)
			return 1;
		p=g->adjlist[j].firstarc;
		while(p!=NULL){
			if(visit[p->adjvex]==0){
				rear=(rear+1)%maxsize;
				que[rear]=p->adjvex;
				visit[p->adjvex]=1;
			}
			p=p->nextarc;
		}
	}
	return 0;
}

练习：输出u到v节点的所有简单路径

图用邻接表表示。从节点u出发，dfs图中节点，当访问到v时输出该搜索路径上所有节点。因此需设置一个path数组存放路径上的节点，d表示路径长度。

void findpath(agraph *g,int u,int v,int path[],int d){
	int w,i;
	arcnode *p;
	d++;
	path[d]=u;
	visited[u]=1;
	if(u==v)print(path[]);
	p=g->adjlist[u].firstarc;
	while(p!=NULL){
		w=p->adjvex;
		if(visited[w]==0)findpath(g,w,v,path,d);
		p=p->nextarc;
	}
	visited[u]=0;//撤回操作，使该点可以重新使用。
}

练习：判断无向图是否是一棵树，是返回1，否返回0

思路：无向图是否是一棵树的条件是有n个顶点，n-1条边的连通图。

void dfs2(agraph *g,int v,int &vn,int &en){
	arcnode *p;
	visit[v]=1;
	++vn;
	p=g->adjlist[v].firstarc;
	while(p!=NULL){
		++en;
		if(visit[p->adjvex]==0)
			dfs2(g,p->adjvex,vn,en);
		p=p->nextarc;
	}
}
int g_is_tree(agraph *g){
	int vn=0,en=0,i;
	for(i=0;i<g->n;i++)
		visit[i]=0;
	dfs2(g,1,vn,en);
	if(vn==g->n&&(g->n-1)==en/2)//en/2是因为无向图，每个顶点都会访问一次该顶点邻接的边，造成访问了2遍所有边
		return 1;
	else return 0;
}

练习：输出有向图的根节点

若r节点到有向图g的每个节点都有路径可达，则为g的根节点。如果有向图g有根，则打印出所有根节点的值。假设图存在邻接表g中。

//采用dfs分别对每个节点进行一次，检查是否到达了n个节点
int visit[maxsize],sum;
void dfs(Agraph *g,int v){
	Arcnode *p;
	visit[v]=1;
	++sum;
	p=g->adjlist[v].firstarc;
	while(p!=NULL){
		if(visit[p->adjvex]==0)
			dfs(g,p->adjvex);
		p=p->nextarc;
	}
}
void print_root(Agraph *g){
	for(int i=0;i<g.n;i++){
		sum=0;
		for(int j=0;j<g.n;j++)visit[j]=0;
		dfs(g,i);
		if(sum==g.n)cout<<i<<" ";
	}
}

练习：判断有向图中是否有回路，并输出回路顶点序列

判断一个有向图是否存在回路，除了采用拓扑算法以外，还可以使用深度优先搜索算法，本算法改编自“用邻接矩阵表示的深度优先搜索算法”，即DFS算法。

拓扑排序的算法步骤

求出所有顶点的入度，可以附设一个存放各顶点入度的数组indegree[]
遍历数组indegree[],如果有顶点的入度为零，便将顶点依次入队或者入栈
当栈或者队列不为空时，一直重复下面两个操作
1）进行出栈或者出队的操作，这里假设操作顶点为v
2）将与顶点v邻接的所有顶点的入度减一，如果出现入度为0的顶点，便进行入栈或者入队操作
若此时输出的顶点数小于有向图的顶点数，则说明有向图中存在回路，否则输出的顶点的顺序即为一个拓扑序列；也就是说当剩余顶点的入度都>0时，拓扑排序算法无法再继续，故不可能输出所有顶点。

dfs方法：
有向图在DFS中增加一个no数组记录dfs函数层数，标志着节点访问的先后顺序，如果visited=1已访问过，而且no[dfs的当前节点v] != no[j当前节点一条边的邻接点] + 1，表示v,j都访问过且不是之前j->v的那条边。
no[j] = i + 1;表示j点未被访问过，现在准备开始访问j节点，i是v点的no,表示路径中v的下一个节点就是j

还有一种更简单的dfs方法，当遍历这个节点后如果还有剩余边能回到这条遍历路径中的点，则说明有“环”
对于无向图来说，如果检测到visited不为0，可能有两种情况

存在环
存在双向边，因为无向图中的每条边都是双向的，例如a->b->a，需要将其过滤掉。如何过滤？访问某个顶点a时，给其编号i，给a->b的点b编号i+1，如果访问c节点有c->d，而d已经被访问过，查看c的编号是否是d的编号+1，如果是则是一条双向边，过滤掉即可。
对于有向图来说，检测到visited不为0，可能是指向深度优先生成森林中另一棵树上顶点的边，但实际上并未构成回路，所以需要在算法中递归返回时抹去遍历痕迹。如图所示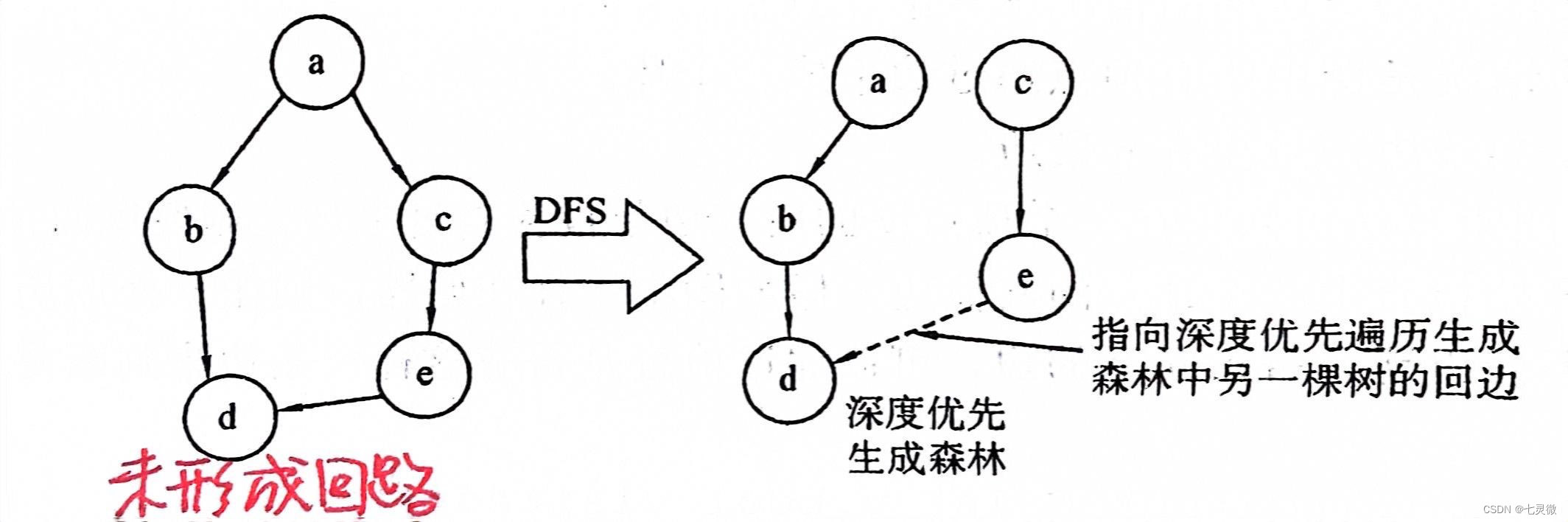

//最简单的版本
bool dfs_circle(Agraph *g,int v,bool visited[]){
	bool flag;
	Arcnode *p;
	visited[v]=true;
	for(p=g.adjlist[v].firstarc;p!=NULL;p=p->next){
		if(visited[p->adjv]==false)
			flag=dfs_circle(g,p->adjv,visited);
		else return true;//说明有一条边有能回到之前路径中的某个顶点了
		if(flag==true)return true;
		visited[p->adjv]=0;//递归返回时抹除遍历痕迹，为什么呢？见上文解析
	}
	return false;
}
//拓扑排序方法
typedef struct VNode{
	char data;
	int count; //入度
	ArcNode *firstarc; //第一条边
}VNode, AdjList[MAX_VERTEX_NUM];
//计算每个顶点的入度
void CntGraphIndegree(ALGraph *pG) {
	ArcNode *p;
	int i;
	for (i=0; i<pG->vernum; i++) {
		for (p=pG->vers[i].firstarc; p; p=p->next) {
			pG->vers[p->adjV].count++;
		}
	}
}
// 拓扑排序，并打印拓扑序列
int TopSort(ALGraph *pG) {
	int i,j;
	int n=0;
	int stack[maxSize],top=-1; //保存当前所有入度为0的顶点
	ArcNode *p;

	CntGraphIndegree(pG); //计算入度
	//将入度为0的顶点压入栈中
	for (i=0; i<pG->vernum; i++) {
		if (pG->vers[i].count==0)
			stack[++top]=i; 
	}

	while (top!=-1) {
		i = stack[top--]; //顶点出栈，等效于在图中删掉
		++n;
		printf("%c ", pG->vers[i].data);

		p=pG->vers[i].firstarc;
		while (p!=NULL) {
			j = p->adjV;
			--(pG->vers[j].count);
			if (pG->vers[j].count==0)
				stack[++top]=j;
			p=p->next;
		}
	}

	if (n==pG->vernum) //拓扑排序后没有剩余顶点
		return 1;
	else //拓扑排序后还有剩余顶点
		return 0;
}

//dfs
#include <stdio.h>
#include <stdlib.h>
#define maxSize 100
 
typedef struct ArcNode
{
	int adjvex;
	struct ArcNode* nextarc;
}ArcNode;
 
typedef struct
{
	char data;
	ArcNode* firstarc;
}VNode;
 
typedef struct
{
	VNode adjlist[maxSize];
	int n, e;//顶点个数和边数
}AGraph;
 
FILE* fp;
void InsertEdge(AGraph* G, int v1, int v2)
{
	ArcNode* p = (ArcNode*)malloc(sizeof(ArcNode));
	p->adjvex = v2;
	p->nextarc = G->adjlist[v1].firstarc;
	G->adjlist[v1].firstarc = p;
 
	/*无向图再加入下面一段代码
	p = (ArcNode*)malloc(sizeof(ArcNode));//不可将p置空，因为要再新插入一个结点，必须给这个结点开辟一个空间
	p->adjvex = v1;
	p->nextarc = G->adjlist[v2].firstarc;
	G->adjlist[v2].firstarc = p;
 	*/
}
 
 
void CreateGraph(AGraph* G)
{
	int nv, ne, i, v1, v2;
	fp = fopen("C:\\CodeBlocksProject\\AG.txt", "r");
	fscanf(fp,"%d%d", &nv, &ne);
	for (i = 0; i < nv; i++)
	{
		G->adjlist[i].firstarc = NULL;
		fscanf(fp, "%c", &G->adjlist[i].data);
	}
 
	for (i = 0; i < ne; ++i)
	{
		fscanf(fp, "%d%d", &v1, &v2);
		InsertEdge(G, v1, v2);
	}
	G->e = ne;
	G->n = nv;
	fclose(fp);
}
int i = -1;
int no[maxSize] = { 0 };
int visit[maxSize] = { 0 };
 
void DFS(AGraph* G, int v)
{
	++i;
	ArcNode* p;
	int j;
	printf("%c ", G->adjlist[v].data);
	visit[v] = 1;
	no[v] = i;
	p = G->adjlist[v].firstarc;
 
	while (p != NULL)
	{
		j = p->adjvex;
		if (visit[j] == 0)
		{
			no[j] = i + 1;
			DFS(G, j);
		}
		else if (no[v] != (no[j] + 1))
		{
			printf("存在回路"); 
		}
		p = p->nextarc;
	}
	--i;
}
 
int main()
{
	AGraph G;
	CreateGraph(&G);
	DFS(&G, 0);
	return 0;
}

练习：无向图中是否存在一条长度为k的简单路径

基于遍历，这里采用dfs，进行变形

int visited[MAXSIZE];
//出发点为i,终点为j，长度为k
int exist_path(ALgraph G,int i,int j,int k){
	if(i==j&&k==0)return 1;
	else if(k>0){
		visited[i]=1;
		for(p=G.vertices[i].firstarc;p;p=p->nextarc){
			int temp=p->adjvex;
			if(!visited[temp]&&exist_path(temp,j,k-1))
				return 1;
		}
		visited[i]=0;//如果当前不存在长度k的到达j点，则这个点后续可能仍需要使用到，要恢复0
	}
	return 0;
}

练习全排列

#include<stdio.h>
int a[10],book[10],n;
void dfs(int step){
	int i;
	if(step==n+1){
		for(i=1;i<=n;i++)
			printf("%d",a[i]);
		printf("\n");
		
		return;	
	}
	for(i=1;i<=n;i++)
	{
		if(book[i]==0){
			a[step]=i;
			book[i]=1;
			dfs(step+1);
			book[i]=0;
		}
	}
	return;
}
int main(){
	scanf("%d",&n);
	dfs(1);
	return 0;
}

练习迷宫问题

找到一条解迷宫的最短路径。

//核心代码
book[startx][starty]=1;
dfs(startx,starty,0);

void dfs(int x,int y int step){
	int next[4][2]={{0,1},{1,0},{0,-1},{-1,0}};//4个方向的x,y变化
	int tx,ty,k;
	if(x==p&&y==q){//end
		if(step<min)min=step;
		return;
	}
	for(k=0;k<4;k++){
		tx=x+next[k][0];
		ty=y+next[k][1];
		if(tx<1||tx>n||ty<1||ty>m)
			continue;
		if(a[tx][ty]==0&&book[tx][ty]==0){//未标记走过且可走
			book[tx][ty]=1;
			dfs(tx,ty,step+1);
			book[tx][ty]=0;
		}
	}
	return;
}

练习 dfs实现有向无环图拓扑排序

有向无环图中任意节点u,v，它们关系必然是三种之一

u是v的祖先，则调用dfs访问时必然先访问u再访问v，则v的dfs函数结束时间先于u的dfs函数结束时间。祖先结束时间必然大于子孙结束时间。
v是u的祖先。同理
u和v没有关系，则u,v在拓扑排序中顺序任意。
由此可得我们可以设置一个time表示结束时间。

bool visited[maxsize];
void dfs_traverse(graph g){
	for(v=0;v<g.vexnum;v++)visited[v]=false;
	time=0;
	for(v=0;v<g.vexnum;v++)
		if(!visited[v])dfs(g,v);
}
void dfs(graph g,int v){
	visited[v]=true;
	visit(v);
	for(w=firstneighbor(g,v);w>=0;w=nextneighbor(g,v,w)){
		if(!visited[w])dfs(g,w);
	}
	time=time+1;
	finish_time[v]=time;
}
//可以按照finish_time中的值从大到小排列结点即可。

练习着色法（floodfill漫水填充法）

改动不多，在dfs基础上加上color即可。

void dfs(int x,int y int color){
	int next[4][2]={{0,1},{1,0},{0,-1},{-1,0}};//4个方向的x,y变化
	int tx,ty,k;
	
	a[x][y]=color;//将能去到的搜索空间均着色
	
	for(k=0;k<4;k++){
		tx=x+next[k][0];
		ty=y+next[k][1];
		if(tx<1||tx>n||ty<1||ty>m)
			continue;
		if(a[tx][ty]==0&&book[tx][ty]==0){//未标记走过且可走
			book[tx][ty]=1;
			dfs(tx,ty,color);
			//不需要撤回操作book[tx][ty]=0;
		}
	}
	return;
}

练习独立区域的数量（求图中独立子图个数）

给一块地图，计算出分割开的区域的数量。运用之前的着色法进行适当改动，可遍历的点全部遍历一边，每遍的颜色不同。

int num=0;//则独立块数为-1*num
for(i=1;i<n;i++){
	for(j=1;j<m;j++){
		if(a[i][j]>0){//可探索点的条件
			num--;//color号
			book[i][j]=1;
			dfs(i,j,num);
		}
	}
}
void dfs(int x,int y int color){
	int next[4][2]={{0,1},{1,0},{0,-1},{-1,0}};//4个方向的x,y变化
	int tx,ty,k;
	
	a[x][y]=color;//将能去到的搜索空间均着色
	
	for(k=0;k<4;k++){
		tx=x+next[k][0];
		ty=y+next[k][1];
		if(tx<1||tx>n||ty<1||ty>m)
			continue;
		if(a[tx][ty]==0&&book[tx][ty]==0){//未标记走过且可走
			book[tx][ty]=1;
			dfs(tx,ty,color);
			//不需要撤回操作book[tx][ty]=0;
		}
	}
	return;
}

*练习水管工游戏

水管工游戏是指如下图中的矩阵中，一共有两种管道，一个是直的，一个是弯的，所有管道都可以自由旋转，最终就是要连通入水口可出水口。其中的树为障碍物。在这里插入图片描述

思路：量化每个水管的状态，弯管有4种状态，直管有2种状态，分别编号成1，2，3，4，5，6；量化水管方向状态，注意进水口和出水口，限制了（1，1）（m,n）的水管状态种类；图例中的情况可以确定（1，1）只能用5号水管，（m,n）只能用1号水管，归结为进水口在左、上、右、下分别用1，2，3，4表示。水管采用的不同决定了下一次探索哪一个位置。

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int n,m,flag,book[51][51];
struct note{
	int x,y;
}s[100];//保存管道路径
int top=0;
void dfs(int x,int y,int front)
{
	int i;
	if(x==n&&y==m+1)//这里的m+1是为了让(n,m)处管道铺设好
	{
		flag=1;
		for(int i=1;i<=top;i++)
		{
			printf("%d,%d\n",s[i].x,s[i].y);//打印从头到尾的路径
		}
		return;
	}
	if(x<1||x>n||y>m||y<1)
	{
		return ;
	}
	if(book[x][y]==1)
		return ;
	book[x][y]=1;
	top++;
	s[top].x=x;
	s[top].y=y;
		if(a[x][y]>=5&&a[x][y]<=6)//两种直管5号，6号
		{
			if(front==1)//进水管在左
			{
				dfs(x,y+1,1);//直管方向不变
			}
			if(front==2)//上
			{
				dfs(x+1,y,2);
			}
			if(front==3)//右
			{
				dfs(x,y-1,3);
			}
			if(front==4)//下
			{
				dfs(x-1,y,4);
			}
		}else if(a[x][y]>=1&&a[x][y]<=4){//弯管1，2，3，4号
			if(front==1)
			{
				dfs(x+1,y,2);//下一个进水方向可能是上或下
				dfs(x-1,y,4);
			}
			if(front==2)
			{
				dfs(x,y+1,1);
				dfs(x,y-1,3);
			}
			if(front==4)
			{
				dfs(x,y+1,1);
				dfs(x,y-1,3);
			}
			if(front==3)
			{
				dfs(x+1,y,2);
				dfs(x-1,y,4);
			}
		}
	book[x][y]=0;//取消标记，尝试下一种可能
	top--;//依然是撤回操作
	return ;	
}
int main(){
	int num=0;
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			cin>>a[i][j];
		}
	}
	dfs(1,1,1);
	if(flag==0)
		cout<<"不存在这种实现方式";
	else cout<<"找到管道铺设方案";
	return 0;
}

广度优先搜索（含队列）

bfs与dfs不同，每一个节点只入队一次，故book数组不需要还原。
更适用于边权值均相同的情况。
BFS需要用到队列，算法执行过程：

任取一个顶点访问，入队，并标记该顶点已访问。
当队列不空时循环执行：出队，依次检查出队顶点的所有邻接顶点，访问未访问的顶点并将其入队。
当队列为空时跳出循环。

void bfs(agragh *g,int v,int visit[maxsize]){
	arcnode *p;
	int que[maxsize],front=0,rear=0;
	int j;
	visit[v]=1;
	rear=(rear+1)%maxsize;
	que[rear]=v;
	while(front!=rear){
		front=(front+1)%maxsize;
		j=que[front];
		p=g->adjlist[j].firstarc;
		while(p!=NULL){
			if(visit[p->adjvex]==0){
				visit[p->adjvex]=1;
				rear=(rear+1)%maxsize;
				que[rear]=p->adjvex;
			}
			p=p->nextarc;
		}
	}
}
//对非连通图遍历，只需将上述遍历函数放在一个循环中，检测图中每一个顶点，如果这个顶点未访问，则从这个顶点开始遍历，否则什么也不做。
void bfs_main(agraph *g){
	int i;
	for(i=0;i<g->n;i++)
		if(visit[i]==0)
			bfs(g,i,visit);
}

bfs算法求解非带权图的单源最短路径问题

这是根据bfs总是按照距离由近到远来遍历图中每个顶点的性质决定的。

#define infty=99999;
void bfs_mindist(graph g,int u){
	for(i=0;i<g.vexnum;++i)d[i]=infty;
	visited[u]=true;
	d[u]=0;
	enqueue(q,u);
	while(!isempty(q)){
		dequeue(q,u);
		for(w=firstneighbor(g,u);w>=0;w=nextneighbor(g,u,w)){
			if(!visited[w]){
				visited[w]=true;
				d[w]=d[u]+1;
				enqueue(q,w);
			}
		}
	}
}

求不带权无向连通图中距顶点v最远的顶点

bfs是由近向远层层扩展遍历图，故bfs遍历过程最后一个点必是距顶点v最远的顶点。

void bfs(agragh *g,int v,int visit[maxsize]){
	arcnode *p;
	int que[maxsize],front=0,rear=0;
	int j;
	visit[v]=1;
	rear=(rear+1)%maxsize;
	que[rear]=v;
	while(front!=rear){
		front=(front+1)%maxsize;
		j=que[front];
		p=g->adjlist[j].firstarc;
		while(p!=NULL){
			if(visit[p->adjvex]==0){
				visit[p->adjvex]=1;
				rear=(rear+1)%maxsize;
				que[rear]=p->adjvex;
			}
			p=p->nextarc;
		}
	}
	return j;//队空时j保存遍历过程最后一个顶点
}

练习迷宫求解

还是之前dfs中的那个问题，用bfs来解决。

//核心代码
//next数组同之前一样。
struct node{
	int x;
	int y;
	int f;//父亲在队列中的编号
	int s;//step步数
};
int main(){
	struct note que[2501];
	int a[51][51]={0},book[51][51]={0};
	int head=1,tail=1;
	que[tail].x=startx;//迷宫入口
	que[tail].y=starty;
	que[tail].f=0;
	que[tail].s=0;
	tail++;
	book[startx][starty]=1;
	flag=0;//标记是否到达目的地点；

	while(head<tail){
		for(k=0;k<3;k++)
		{
			tx=que[head].x+next[k][0];
			tx=que[head].y+next[k][1];
			if(tx<1||tx>n||ty<1||ty>m)
				continue;
			if(a[tx][ty]==0&book[tx][ty]==0){
				book[tx][ty]=1;
				que[tail].x=tx;
				que[tail].y=ty;
				que[tail].f=head;
				que[tail].s=que[head].s+1;
				tail++;
			}
			if(tx==p&&ty==p){
				flag=1;
				break;
			}
		}
		if(flag==1)break;
		head++;//非常重要 忘记则导致搜索无法拓展
	}
}

练习是否存在vi到vj顶点的路径

若从i开始进行一轮遍历完visited[j]=1则表示vi到vj有路径

//bfs实现
int visited[maxsize]={0};
int bfs(algraph g,int i,int j){
	initqueue(q);
	enqueue(q,i);
	while(!isempty(q)){
		dequeue(q,u);
		visited[u]=1;
		if(u==j)return 1;
		for(int p=firstneighbor(g,i);p;p=nextneighbor(g,u,p)){
			if(p==j)return 1;
			if(!visited[p]){
				enqueue(q,p);
				visited[p]=1;
			}
		}
	}
	return 0;
}

拓扑排序

首先要加上记录每个节点的count值，还需要设置一个栈，用来记录当前入度为0的节点，还需设置计数器n记录已经输出的顶点个数。
算法思想：

扫描所有节点，将入度为0的节点入栈
栈不空时循环执行：出栈，将出栈节点输出，n++，将由该顶点引出的所有边入度–，将入度变为0的节点入栈；
重复2至栈空；判断n是否等于图中顶点个数，即是否无环。

bool topological_sort(graph g){
	initstack(s);
	for(int i=0;i<g.vexnum;i++)
		if(indegree[i]==0)push(s,i);
	int count=0;
	while(!isEmpty(s)){
		pop(s,i);
		print[count++]=i;
		for(p=g.vertices[i].firstarc;p;p->nextarc){
			v=p->adjvex;
			if(!(--indegree[v]))push(s,v);
		}
	}
	if(count<g.vexnum)return false;
	else return true;
}

查找

二叉树查找/排序/删除

折半查找的递归算法

最简单的优化

如果未发生更改，则跳出循环。这个最简单的优化运用广泛，见冒泡排序/Bellman-Ford算法等。

输入 or 输出的艺术

scanf("%d %d",&a,&b);//输入区间
 printf("%05d", id)//不足5位在前面补0
printf("%5d",i);//题目要求占5个字符宽
printf("\n");
printf("Sum = %d",sum);

scanf("%d%*c%c%*c%[^\n]]",&N,&c,s)
scanf("%[^\n]%*c",str)

格式	说明	举例输入（解释）
`%*c`	跳过一个字符（通常是另一个分隔符）
`%[^\n]`	读取一整行（直到换行符 `\n`），存入 `s`，不会读入换行符	比如 `"Hello world"` 存入 `s`

注意
向char数组和int数组放入数字再取出来是不一样的：char数组取出要转变成int需要减去’0’

字符数组

字符数组就是char数组，当维度是一维是可以当做“字符串”，当维度是二维时可以当成是字符串数组，即若干字符串。

scanf输入，printf输出
scanf对字符串的输入有%s和%c两种格式。
%c格式用来输入单个字符，它能够识别空格和换行符并将其保存到字符数组中；
%s格式用来输入一个字符串，通过空格和换行来识别一个字符串的结束，使用%s格式输入并保存到字符数组中的字符串是不含空格/换行的。

#include <stdio.h>
int main(){
    char str[10];
    scanf("%s", str);
    printf("%s", str);
    return 0;
}

getchar输入，putchar输出
getchar和putchar分别用来输入和输出单个字符。getchar可以识别换行符和空格并将其保存。

#include <stdio.h>
int main(){
    char c1, c2, c3;
    c1 = getchar();
    c2 = getchar();
    c3 = getchar();		    
    putchar(c1);
    putchar(c2);
    putchar(c3);
    return 0;
}

gets输入，puts输出
gets用来输入一行字符串并将其存放于一维数组（或二维数组的一维）中，读取字符串直到换行符结束，但换行符会被丢弃并在末尾添加‘\0’，
gets可识别空格并输入保存。puts函数会自动换行。
需要注意的是：gets函数会无限读取，不会判断上限，所以程序员应该确保buffer的空间足够大，以便在执行读取操作时不会发生溢出。如果溢出，多出来的字符会被写入到堆栈中，这就覆盖了堆栈原有的内容，破坏一个或多个不相关变量的值。所以推荐更安全的fgets()

gets / scanf对比
gets(s) 会读取整行，直到遇到换行符，然后把换行符丢弃，在末尾加 \0。
scanf(“%s”, s) 只读取第一个“单词”，在遇到空白字符（如空格）就停止，不会读取整行。

#include <stdio.h>
int main(){
    char str1[20];
    char str2[5][10];
    gets(str1);
    for(int i = 0; i < 3; i ++){
        gets(str2[i]);
    }
    puts(str1);
    for(int i = 0; i < 3; i ++){
        puts(str2[i]);
    }
    return 0;
}

吞空格、吞行

若输入样例多含了空格/回车换行符，用getchar();吞掉。

%d,%05d,%-5d,%.5d的区分

%d是普通的输出
%5d是将数字按宽度为5，采用右对齐方式输出，若数据位数不到5位，则左边补空格
%-5d就是左对齐
%05d，和%5d差不多，只不过左边补0
%.5d从执行效果来看，和%05d一样
%5.2f 宽度为5的浮点数，小数点保留2位，不够5位右对齐输出

printf("%04d-%02d-%02d\n",year,month,day)

%d %ld %lld

%d 输出的是 int,
%ld 输出的是 long,
%lld 输出的是 long long;

gets/puts/fgets

gets用来输入一行字符串(注意:gets识别换行符\‘0’作为输入结束，因此 scanf完一个整数后，如果要使用gets，需要先用 getchar接收整数后的换行符)，并将其存放于一维数组(或二维数组的一维)中；或者删去末尾的’0’

puts用来输出一行字符串，即将一维数组(或二维数组的一维)在界面上输出，并紧跟一个换行。

虽然用 gets() 时有空格也可以直接输入，但是 gets() 有一个非常大的缺陷，即它不检查预留存储区是否能够容纳实际输入的数据，换句话说，如果输入的字符数目大于数组的长度，gets 无法检测到这个问题，就会发生内存越界，所以编程时建议使用 fgets()。

fgets() 虽然比 gets() 安全，但安全是要付出代价的，代价就是它的使用比 gets() 要麻烦一点，有三个参数。它的功能是从 stream 流中读取 size 个字符存储到字符指针变量 s 所指向的内存空间。它的返回值是一个指针，指向字符串中第一个字符的地址。# include <stdio.h>
char *fgets(char *s, int size, FILE *stream);
其中：s 代表要保存到的内存空间的首地址，可以是字符数组名，也可以是指向字符数组的字符指针变量名。size 代表的是读取字符串的长度。stream 表示从何种流中读取，可以是标准输入流 stdin，也可以是文件流，即从某个文件中读取，这个在后面讲文件的时候再详细介绍。标准输入流就是前面讲的输入缓冲区。所以如果是从键盘读取数据的话就是从输入缓冲区中读取数据，即从标准输入流 stdin 中读取数据，所以第三个参数为 stdin。
不用数字符长度！fget() 函数中的 size 如果小于字符串的长度，那么字符串将会被截取；如果 size 大于字符串的长度则多余的部分系统会自动用 ‘\0’ 填充。所以假如你定义的字符数组长度为 n，那么 fgets() 中的 size 就指定为 n–1，留一个给 ‘\0’ 就行了。

cin、cin.get()、cin.getline()、getline()

根据cin>>sth 中sth的变量类型读取数据，这里变量类型可以为int，float,char,char*,string等诸多类型。这一输入操作，在遇到结束符（Space、Tab、Enter）就结束，且对于结束符，并不保存到变量中。注意：最后一个enter也在缓冲区。

cin.get(字符数组名，接收长度，结束符)
其中结束符意味着遇到该符号结束字符串读取,默认为enter，读取的字符个数最多为（长度 - 1），因为最后一个为’\0’。要注意的是，cin.get(字符数组名，接收长度，结束符)操作遇到结束符停止读取，但并不会将结束符从缓冲区丢弃。

输入字符后，其结束符（如默认的Enter）会保留在缓冲区中，当下次读入时，又会再读入，此时就可以用到cin.get()读掉输入缓冲区不需要的字符

cin.getline(字符数组名，接收长度，结束符)
其用法与cin.get(字符数组名，接收长度，结束符)极为类似。cin.get()当输入的字符串超长时，不会引起cin函数的错误，后面若有cin操作，会继续执行，只是直接从缓冲区中取数据。但是cin.getline()当输入超长时，会引起cin函数的错误，后面的cin操作将不再执行。
cin.get()每次读取一整行并把由Enter键生成的换行符留在输入队列中，需要用cin.get(ch);读掉它。然而cin.getline()每次读取一整行并把由Enter键生成的换行符抛弃。

getline(istream is,string str,结束符)
同样，此处结束符为可选参数（默认依然为enter）。然而，getline()与前面的诸多存在的差别在于，它string库函数下，而非前面的istream流，所有调用前要在前面加入#include< string>。与之对应这一方法读入时第二个参数为string类型，而不再是char*，要注意区别。另外，该方法也不是遇到空白字符(tab, space, enter(当结束符不是默认enter时))就结束输入的，且会丢弃最后一个换行符。

while((c=getchar())!=‘\n’){ //注意这个是使getchar结束符为换行

练习1 L1-025 正整数A+B

题目：求两个正整数A和B的和，其中A和B都在区间[1,1000]。稍微有点麻烦的是，输入并不保证是两个正整数。
输入格式：
输入在一行给出A和B，其间以空格分开。问题是A和B不一定是满足要求的正整数，有时候可能是超出范围的数字、负数、带小数点的实数、甚至是一堆乱码。
注意：我们把输入中出现的第1个空格认为是A和B的分隔。题目保证至少存在一个空格，并且B不是一个空字符串。
输出格式：
如果输入的确是两个正整数，则按格式A + B = 和输出。如果某个输入不合要求，则在相应位置输出?，显然此时和也是?。
输入样例1：
123 456
输出样例1：
123 + 456 = 579
输入样例2：
22. 18
输出样例2：
? + 18 = ?
输入样例3：
-100 blabla bla…33
输出样例3：
? + ? = ?

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<stdlib.h>
#include<algorithm>
#include<cmath>
using namespace std;

int f(string a){
	for(int i=0;i<a.length();i++)
	{
		if(a[i]<48||a[i]>57)return 0;
	}
	return 1;
}
int s(string a){
	int sum=0;
	int k=1;
	for(int j=a.length()-1;j>=0;j--)
	{
		int xs=0;
		xs+=(int)a[j];
		xs-=48;
		xs*=k;
		sum+=xs;
		k*=10;
	}
	return sum;
}
int main()
{
  string a,b;
  a="";
  int absum=0;
  char c;
  c=getchar();
  while(c!=' '&&c!='\n'){
  	a+=c;
  	c=getchar();
  }
  
  getline(cin,b);
  if(f(a)==0)a="?";
  if(f(b)==0)b="?";
  if(s(a)>1000||s(a)<1) a="?";
  if(s(b)>1000||s(b)<1) b="?";
  
  if(a!="?"&&b!="?"){
  
  	absum=s(a)+s(b);
  	cout<<a<<" + "<<b<<" = ";
  	cout<<absum<<endl;
  	
  }
  else 	{
  		cout<<a<<" + "<<b<<" = ?";
  		
  }
    return 0;
}

练习2 L1-032 Left-pad

#include<bits/stdc++.h>
using namespace std;
int main() {
	int n; char a; string s;
	cin>>n>>a;
	getchar();//读掉回车
	getline(cin,s);//读字符串
	if(n>=s.length()) {
		for(int i=0;i<n-s.length();i++)
		cout<<a;
		cout<<s;	
	}
	else
		for(int i=s.length()-n;i<s.length();i++) cout<<s[i];		
return 0 ;}

ascii码

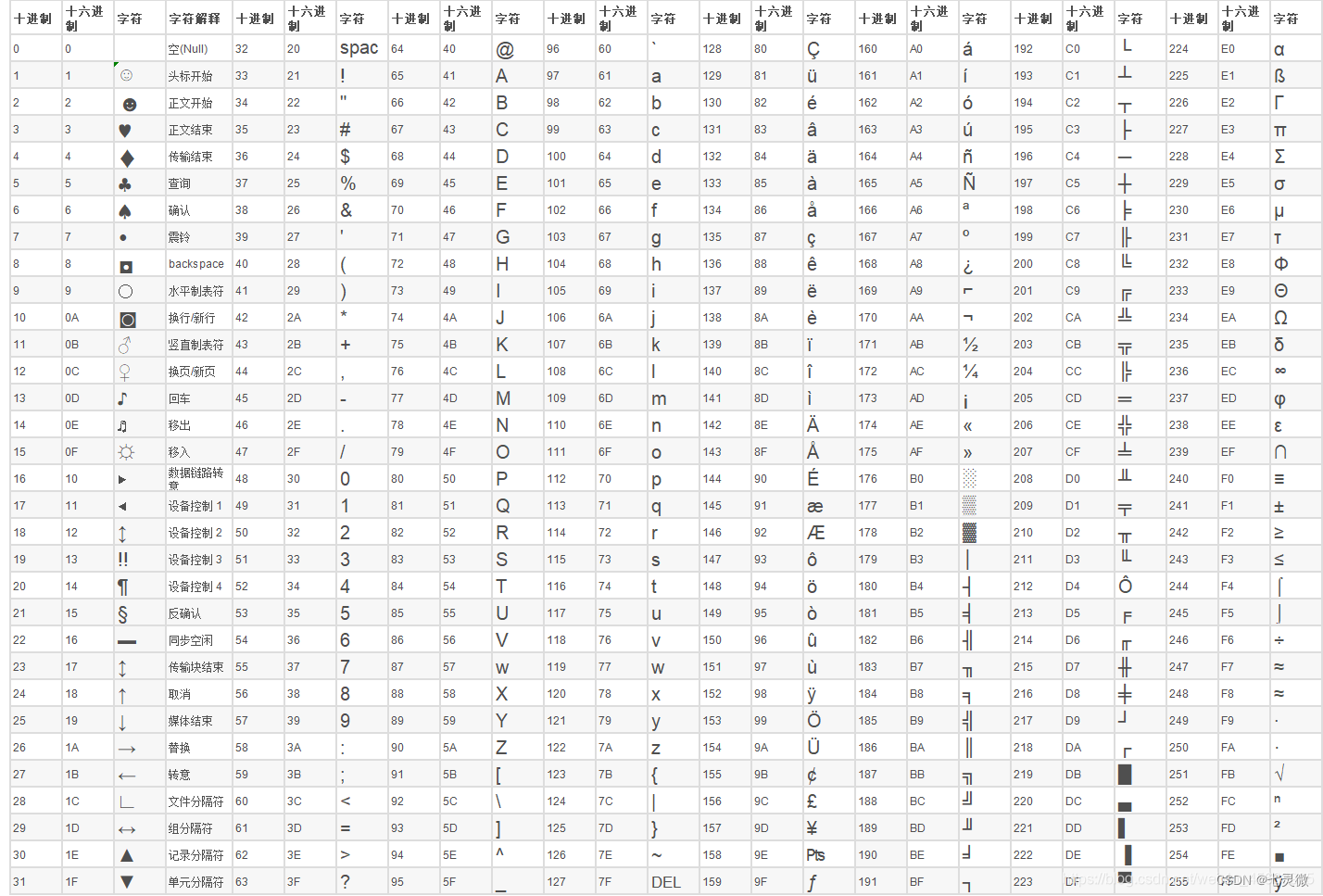
在这里插入图片描述

练习：输入一个字符串，求它包含多少个单词。单词间以一个或者多个空格分开。第一个单词前，最后一个单词后也可能有0到多个空格。比如：" abc xyz" 包含两个单词，"ab c xyz " 包含3个单词。

int get_word_num(char* buf)
{
	int n = 0;   
	int tag = 1; 
	char* p = buf;
	// *p==0空 *p==13回车 *p==10换行
	for(;*p!=0 && *p!=13 && *p!=10;p++){
		if(*p==' ' && tag==0) tag=1;
		if( *p!=' ' && tag==1  ) { n++; tag=0; }  
		 //当前一位是空格，但后一位不是空格时就代表一个单词出现，n++。 
	}
	
	return n;
}

int main()
{
	char buf[1000];
	fgets(buf,1000,stdin);
	
	printf("%d\n", get_word_num(buf));
	return 0;
}

各种数字运算

位逻辑运算符：&｜^~与或非补
abs(i) //math.h
fabs(i)浮点数求绝对值//stdio.h
sin()//三角函数
isalpha(c) //头文件ctype.h
isdigit(c)
isalnum(c)
int的取值范围为: -2^31——2^31-1,即-2147483648——2147483647 是一个十位数 

这是计算机中一种科学计数法的表示形式：
1e9 = 1*(10^9) = 1000000000；
例如：9e8 = 9*(10^8) = 900000000；
e表示10，e后面的数字表示次方，e的多少次方。

勾股定理

已知直角三角形的斜边是某个整数，并且要求另外两条边也必须是整数。
求满足这个条件的不同直角三角形的个数。
【数据格式】
输入一个整数 n (0<n<10000000) 表示直角三角形斜边的长度。
要求输出一个整数，表示满足条件的直角三角形个数。
例如，输入：
5
程序应该输出：
1
再例如，输入：
100
程序应该输出：
2
再例如，输入：
3
程序应该输出：
0
要注意的是平方之后容易超出int的范围，用上longlong，最好不要用double，double在判等的时候精度问题容易错。暴力的时候穷举到 c/sqrt(2)就行了，也是一个优化点。

#include<stdio.h>
#include<math.h>
int main()
{
	long long aa,bb,cc;
	int a,b,c,count=0;
	scanf("%d",&c);
	cc = c*c;
	for(a=1;a<c/sqrt(2);a++)
	{
		aa = a*a;
		b = sqrt(cc-aa);//b等于斜边的平方-另一边的平方再开方
		if(b*b+aa==cc)
		{
			count++;//加1 
		} 
	}
	printf("%d\n",count);
	return 0; 
}

有如下的加法算式。其中每个汉字代表一个数字，注意对齐。求“让我怎能过大年 ”所代表的整数。所有数字连在一起，中间不要空格。

               年
             大年
           过大年
         能过大年
       怎能过大年
     我怎能过大年
+  让我怎能过大年
------------------
   能能能能能能能

暴力？套7层循环，复杂度太高。

膜运算

#include<stdio.h>
int main()
{
	int sum;
	int i;
	int temp;
	int a,b,c,d,e,f,g;//代表每一位上的数字 
	for(i=9992299;i>=1000000;i--)
	{
		a = i%10;//个位
		b = i/10%10;//十位 
		c = i/100%10;//百位 
		d = i/1000%10; //千位
		e = i/10000%10;//万位
		f = i/100000%10;//十万位
		g = i/1000000%10;//百万位 
		
		//printf("%d\t%d\t%d\t%d\t%d\t%d\t%d\n",a,b,c,d,e,f,g);
		//break; 
		
		temp=d*1000000+d*100000+d*10000+d*1000+d*100+d*10+d*1; 
		//printf("%d\n",temp);
	    //break;
	    
		a=0+a*1;
		b=a+b*10;
		c=b+c*100;
		d=c+d*1000;
		e=d+e*10000; 
		f=e+f*100000;
		g=f+g*1000000;  //也可以直接g=i; 
		
		//printf("%d\t%d\t%d\t%d\t%d\t%d\t%d\n",a,b,c,d,e,f,g);
		//break; 
		
		sum=a+b+c+d+e+f+g;
		if(sum==temp)
		{
			printf("%d\n",i);
			break;
		}	
	}
	return 0;
}

连续因子

一个正整数 N 的因子中可能存在若干连续的数字。例如 630 可以分解为 3×5×6×7，其中 5、6、7 就是 3 个连续的数字。给定任一正整数 N，要求编写程序求出最长连续因子的个数，并输出最小的连续因子序列。

输入格式：
输入在一行中给出一个正整数 N（1<N<231）。

输出格式：
首先在第 1 行输出最长连续因子的个数；然后在第 2 行中按因子1因子2……*因子k 的格式输出最小的连续因子序列，其中因子按递增顺序输出，1 不算在内。

输入样例：
630
输出样例：
3
567

思想：从1乘到N，每乘一次判定当前乘积prd是否为N的因子，即N%prd是否为0，若为0，比较上一次乘积因子序列的长度，若大于，则记录。
不断更新乘积因子序列长度，直到最后一个因子为N。当然，最需要注意的是最外层的循环变量i判定条件必须为i<=sqrt(n),如果是i*i<=n，则最后一个测试点会不过。本人猜测可能是平台的问题。虽然看上去很暴力，但此算法最后一个测试点耗时仅5ms。
最小的连续因子序列也就是说让start起始因子尽可能大。

#include<iostream>
#include<cmath>
using namespace std;
typedef long long ll;
int main()
{
	ll n;
	cin>>n;
	ll prd=0;//定义乘积 
	int start=0,len=0;//定义最终得到序列开始的因子，序列的长度 
	for(int i=2;i<=sqrt(n);i++)//i从2到根号n 
	{
		prd=1;
		for(int j=i;prd*j<=n;j++)//从j开始一直乘到N为止，每次乘积判定是否小于等于N，若超过N，则结束循环 
		{
			prd*=j;//乘积迭代 
			if(n%prd==0&&j-i+1>len)//如果当前乘积为N的乘积因子且长度大于上一次 
			{//更新序列起始因子和长度 
				start=i;
				len=j-i+1;
			}
		}
	}
	if(start==0)//若起始因子为0，说明N为质数，因为质数=1*本身，而循环最多能表示1*本身的根号 
	{
		start=n;
		len=1;
	}
	cout<<len<<'\n'<<start;
	for(int i=start+1;i<start+len;i++)//输出，如果因子只有一个只输出一个 
		cout<<'*'<<i;
	return 0;
}

最简单的gcd（最大公约数）

LL gcd(LL a,LL b)///求最大公约数  
{  
    return a%b==0?b:gcd(b,a%b);  //求出a和b的最大公约数，并返回 
}

n个分数求和

本题的要求很简单，就是求N个数字的和。麻烦的是，这些数字是以有理数分子/分母的形式给出的，你输出的和也必须是有理数的形式。

输入格式：
输入第一行给出一个正整数N（≤100）。随后一行按格式a1/b1 a2/b2 …给出N个有理数。题目保证所有分子和分母都在长整型范围内。另外，负数的符号一定出现在分子前面。

输出格式：
输出上述数字和的最简形式 —— 即将结果写成整数部分分数部分，其中分数部分写成分子/分母，要求分子小于分母，且它们没有公因子。如果结果的整数部分为0，则只输出分数部分。

输入1：
5
2/5 4/15 1/30 -2/60 8/3

输出:
3 1/3

#include<cstdio>  
#include<cstring>  
#include<cmath>  
#include<algorithm>  
#define LL long long  //给long long类型起一个别名 LL 
using namespace std;  

LL gcd(LL a,LL b)///求最大公约数  
{  
    return a%b==0?b:gcd(b,a%b);  //求出a和b的最大公约数，并返回 
}  

int main()  
{  
    LL t,a[101],b[101],s1=0,s2=0;  
    scanf("%lld",&t);  //t:输入你要计算的是多少个分数求和 
    for(int i=0; i<t; i++)  
        scanf("%lld/%lld",&a[i],&b[i]);  //依次输入要计算的分数  3/8 1/4 1/16
    s2=b[0];  //第一个分数的分母，8 
    for(int i=1; i<t; i++)  
        s2=s2/gcd(s2,b[i])*b[i];///求出所有分数的公分母，即例如 3/8  1/4  gcd反回4   公分母就是(8*4)/4
        //s2是所有分数的公分母 
    for(int i=0; i<t; i++)  
        s1+=s2/b[i]*a[i];///求分子总和 例如:公分母16 ，(16/8)*3 就是6是第一个分数的分子  (公分母）/分母*分子 
        //是s1是总的分子 
    LL n=s1/s2,m=abs(s1%s2);  //n就是结果的整数部分， m是余数部分
    if(m==0) printf("%lld\n",n);  //结果为整数，没有小数部分，直接输出n 
    else  
    {  
        if(n!=0)printf("%lld ",n);  //n不为0，有整数部分，输出整数部分 
        if(s1<0&&n==0)printf("-");  //如果n等于0，且分子是负数，结果为一个负的真分数，输出负号 
        printf("%lld/%lld\n",m/gcd(s2,m),s2/gcd(s2,m));  //输出分数，例如m是6  6和18的最大公约数是6  6/6=1 18/6=3  即结果1/3 
    }  
    return 0;  
}

最简单的循环移位

int fun(int n)//一次循环移位
{
	int a = n%10;//取出最后一位  比如12345得出a=5,同理%100取出倒数第二位
	int b = n/10;//取出前面4位                b=1234
	return a*10000+b; //经典的循环返回， 5*10000+1234=51234
} 

//封装好的多次循环移位
void roll(int n,int cnt)//n要循环移位的数，cnt循环移动几次
{
    int n_=n;
    int a,b,sum;
    int i=0;
    while(i<cnt)
    {
        a = n_%10;//取出最后一位  比如12345得出a=5,同理%100取出倒数第二位
        b = n_/10;//取出前面4位   b=1234
        sum=a*10000+b;
	    std::cout<<sum<<std::endl;
        n_=sum;
        i++;
    }
}

练习题 1193是个素数，对它循环移位后发现：1931,9311,3119也都是素数，这样特征的数叫：循环素数。你能找出具有这样特征的5位数的循环素数吗？当然，这样的数字可能有很多，请写出其中最大的一个。注意：答案是个5位数，不要填写任何多余的内容。
我的思路：99999 ~ 11111的n的降序循环里面套一层五次循环移位的循环顺便判断一个函数即判断是否是素数（模2 ~ 根号n的循环如果都模不等于0则返回它）然后程序结束

6位小数double “%6lf”

如果x的x次幂结果为10（参见【图1.png】），你能计算出x的近似值吗？显然，这个值是介于2和3之间的一个数字。请把x的值计算到小数后6位（四舍五入），并填写这个小数值。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<stdlib.h>
#include<algorithm>
#include<cmath>
using namespace std;

int main()
{
	double a=2.0;
	for(;a<3;a+=0.0000001)//要比要求的6位小数多出一位才能四舍五入
	{
		if(fabs(pow(a,a)-10.0)<0.000001)
		break;
	}
	printf("%6lf",a); //lf是double格式 
    return 0;
}

全排列

算法思想：
将第一个元素分别确定为1~n，即每次将元素与第一个元素进行交换，分别作为一次第一元素。待后面位置全排列后再将它们交换回来，准备做下一次的全排列。
然后对后面的位置进行全排列。按照分治法，一直向后分解。
如果题目中排列数中有重复元素，则判断是否相同，不相同才交换。
基本操作就是依次交换，先确定第一个字符，然后n-1个字符进行全排列，对n-1个字符全排列，先确定第二个字符，对n-2个字符全排列。。。。到第n-2个字符时，就是将最后两个字符交换位置。

//版本1
void perm(int a[],int p,int q){//对下标p~q的数组值进行全排列
	if(p==q)
		print_array(a,q-1);
	else{
		int i;
		for (i=p;i<=q;i++){
			swap(a,p,i);//交换a[p]和a[i]
			perm(a,p+1,q);
			swap(a,p,i);
		}
}
//版本2
#define elemtype int
int _start=0,_end=2;
int list[4]={1,2,3};
void swap(elemtype *a, elemtype *b) {
    elemtype temp;
    temp = *a;
    *a = *b;
    *b = temp;
}
int IsSwap(elemtype list[], int l, int r) {
    for (int i = l; i < r; i++) {
        if (list[i] == list[r])
            return 0;
    }
    return 1;
}
void qpl(elemtype list[], int l, int r) {
    int j;
    if (l == r) {
        for (int a = _start; a <=_end; a++)
            printf("%d", list[a]);
        printf("\n");
    }
    for (j = l; j <= r; j++) {
        if(IsSwap(list,l,j))//如果字符序列中有重复值时的改进
        {	swap(&list[j], &list[l]);
            qpl(list, l + 1, r);
            swap(&list[j], &list[l]);//撤回操作
        }else	continue;
		/*没有重复值时的代码如下
		swap(&list[j], &list[l]);
	    qpl(list, l + 1, r);
	    swap(&list[j], &list[l]);//撤回操作
		*/
    }
}
int main()
{
    qpl(list,0,2);
    return 0;
}

组合数

组合数公式c(n,m)=n!/(m!(n-m)!)

long c=1;int m,n;
for(int i=1;i<=n;i++)
	c=c*(m-i+1)/i;

算法思想：一共从n个中选取m个数组成排列。或利用阶层相除；
首先分别将n个元素放入第一位，然后接下来递归，只不过位置仅有m个。

//从1～n范围中选出m个数作为序列，求不同序列的个数。
void dfs(ll num,ll len,ll n,ll m){
//起点，当前选中长度，总共可选数个数，仅有的位置数	
	if(len==m){//选全m个数 
		for(ll i=1;i<=m-1;i++){
			cout<<a[i]<<" ";
		}
		cout<<a[m]<<endl;
		return ; 
	}
	if(num==n){//没有选全m个数，但是数已经超过n，return； 
		return ;
	}
	for(ll i=num+1;i<=n;i++){//寻找后面的数字 i即放入的数字取值 
//当取满之后再退回继续取，如果已经出现num==n但没选全情况则换下一个数做第一位
		a[++len]=i;//选进  从下标1开始存
		dfs(i,len,n,m);
		len--;//踢出 
	}
	return ;
}
 
int main(){
	ll n,m;
	cin>>n>>m;
	dfs(0,0,n,m);
	return 0;
}

打印形状——沙漏

***** 第一层 空格数0 
 ***  第二次 空格数1
  *   第三层 空格数2
 *** 
*****
给定任意N个符号，不一定能正好组成一个沙漏。要求打印出的沙漏能用掉尽可能多的符号。
1.首先确定最多用多少个符号？
2n^2-1 n逐渐递增，大于N时跳出，注意保存n，它是三角形的层数。
2.打印倒三角 倒三角层数是倒着排的，第三层，第二层，第一层。第n层符号数有2n-1个。当层数小于n层，假设为a层时需要先输出n-a个空格，再输出符号；行末尾的空格不用管，直接回车。
3.打印正三角 同理

二项式系数&杨辉三角

二项式的系数规律其排列规律：
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
要求建立N行的杨辉三角形。

#define N 8
int main()
{
	int a[N][N];
	int i,j;
	
	for(i=0; i<N; i++){
		a[i][0] = 1;
		a[i][i] = 1;
	}
	
	for(i=1; i<N; i++){
		for(j=1; j<i; j++)  a[i][j]=a[i-1][j-1]+a[i-1][j];
	}
	
	for(i=0; i<N; i++){
		for(j=0; j<=i; j++)	printf("%-5d", a[i][j]);
		printf("\n");
	}
	
	return 0;
}