1450C2 Errich-Tac-Toe (Hard Version)（思维）

最新推荐文章于 2021-07-13 20:24:20 发布

原创最新推荐文章于 2021-07-13 20:24:20 发布 · 361 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#Codeforces #1450C2 #Errich-Tac-Toe #思维

个人题解专栏收录该内容

32 篇文章

订阅专栏

1450C2 Errich-Tac-Toe (Hard Version)（思维）

Codeforces Global Round 12

C2. Errich-Tac-Toe (Hard Version)

题面：Errich-Tac-Toe (Hard Version)

题意：有一个 $n * n$ 的棋盘，上面每个格子内要么是空的，要么包含棋子 $X$ 或者棋子 $O$ ，如果存在连续三个 $X$ 或者连续三个 $O$ 在同一排或者同一列则该局面不是平局，否则就是平局。现在可以进行翻转操作，一次可以将一个 $X$ 变成 $O$ 或者将一个 $O$ 变成 $X$ ，现在问如何通过不超过 $\lfloor\frac{k}{3}\rfloor$ 次操作让局面变成平局，其中 $k$ 是棋盘中非空格子的数量。

范围： $\le n \le 300$ 。

分析：我们可以思考出这样一个结论：如果我们能让连续的三个棋子中至少出现一个 $X$ 和一个 $O$ ，那么就能避免三个连续相同棋子的情况，形成平局。

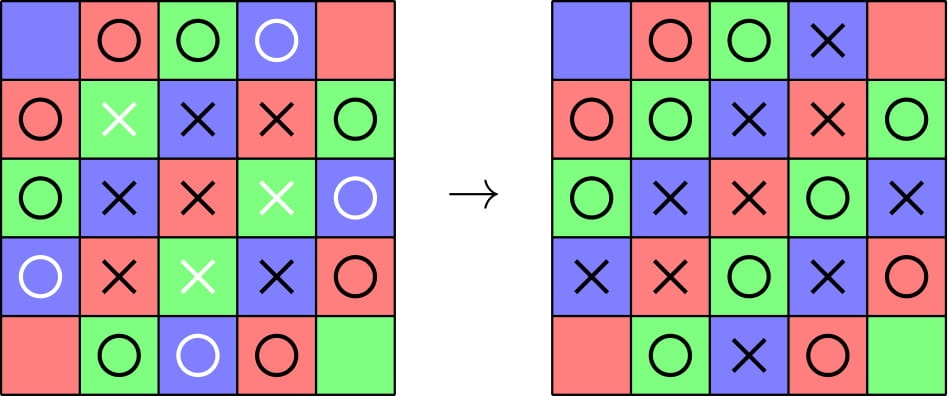
（相当于我们需要选择间隔相同的 $X$ 对角线与 $O$ 对角线对棋盘进行分割，避免出现三个棋子同色的情况）

同一排或者同一列三个连续的棋子满足 $\% 3 == 0, 1, 2$ ，因此我们可以按照 $(i+j)\%3$ 来对所有的 $X$ 与 $O$ 进行统计，假设数量为 $x 0, x 1, x 2, o 0, o 1, o 2$ ，显然 $k = x 0 + x 1 + x 2 + o 0 + o 1 + o 2$ ，需要使得连续的三个棋子中至少出现一个 $X$ 和一个 $O$ ，那么我们需要在 $x 0, x 1, x 2$ 中选择一个并且在 $o 0, o 1, o 2$ 中选择一个位置不同的进行修改操作，找到最小的 $x i + o j$ ，它一定满足 $xi+oj\le \lfloor\frac{k}{3}\rfloor$ ，最后根据选择的两个数字对棋盘棋子进行翻转输出即可。

Code：

#include <bits/stdc++.h>
#define int long long
#define double long double
using namespace std;
 
inline int read()
{
    int s = 0, w = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9')
    {
        if (ch == '-')
            w = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9')
        s = s * 10 + ch - '0', ch = getchar();
    return s * w;
}
 
const int MAXN = 300 + 10;
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const double eps = 1e-9;
const double PI = acos(-1.0);
 
int n, m, k;
 
char arr[MAXN][MAXN];
 
int num_x[3], num_y[3];
 
signed main()
{
    int T = read();
    while (T--)
    {
    	memset(num_x, 0, sizeof(num_x));
    	memset(num_y, 0, sizeof(num_y));
        n = read();
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < n; j++)
            {
            	cin >> arr[i][j];
            	if (arr[i][j] == 'X') num_x[(i + j) % 3]++;
            	else if (arr[i][j] == 'O') num_y[(i + j) % 3]++;
            }
        }
        int idx1 = 0, idx2 = 0;
        int minV = INF;
        for (int i = 0; i < 3; i++)
        {
        	for (int j = 0; j < 3; j++)
        	{
        		if (i == j) continue;
        		if (minV > num_x[i] + num_y[j])
        		{
        			minV = num_x[i] + num_y[j];
        			idx1 = i, idx2 = j;
        		}
        	}
        }
        for (int i = 0; i < n; i++)
        {
        	for (int j = 0; j < n; j++)
        	{
        		if (arr[i][j] == 'X' && (i + j) % 3 == idx1)
        		{
        			arr[i][j] = 'O';
        		}
        		else if (arr[i][j] == 'O' && (i + j) % 3 == idx2)
        		{
        			arr[i][j] = 'X';
        		}
        		cout << arr[i][j];
        	}
        	cout << endl;
        }
    }
    return 0;
}