LightOJ 1203 Guarding Bananas（凸包，内角）

Guarding Bananas

Once there was a lazy monkey in a forest. But he loved banana too much. One day there was a storm in the jungle and all the bananas fell from the trees. The monkey didn’t want to lose any of the bananas. So, he wanted to find a banana such that he can eat that and he can also look after the other bananas. As he was lazy, he didn’t want to move his eyes too wide. So, you have to help him finding the banana from where he can look after all the bananas but the degree of rotating his eyes is as small as possible. You can assume that the position of the bananas can be modeled as 2D points.

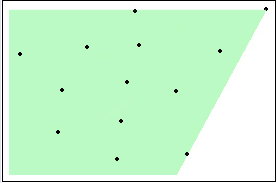
Here a banana is shown, from where the monkey can look after all the bananas with minimum eye rotation.

Input
Input starts with an integer T (≤ 13), denoting the number of test cases.

Each case starts with a line containing an integer n (1 ≤ n ≤ 105) denoting the number of bananas. Each of the next n lines contains two integers x y (-109 ≤ x, y ≤ 109) denoting the co-ordinate of a banana. There can me more than one bananas in the same co-ordinate.

Output
For each case, print the case number and the minimum angle in degrees. Errors less than 10-6 will be ignored.

Sample Input

2
1
4 4
4
0 0
10 0
10 10
2 1

Sample Output

Case 1: 0
Case 2: 45.0000000

Note
Dataset is huge. Use faster I/O methods.

题意
给你n个点找一个点能够以最小的角度看到所有的点

题解
该最小角的顶点，明显知道肯定是在凸包上，如果在凸包内需要环顾360度，所以枚举凸包上点，找到最小内角即可，模板题

代码

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <queue>
#include <cmath>
#include <string>
#include <cstring>
#include <map>
#include <set>
#include <math.h>
#include <unordered_map>
//#include <tr1/unordered_map>

using namespace std;
#define me(x,y) memset(x,y,sizeof x)
#define MIN(x,y) x < y ? x : y
#define MAX(x,y) x > y ? x : y

typedef long long ll;
typedef unsigned long long ull;

const int maxn = 1e5+10;
const double INF = 0x3f3f3f3f;
const double eps = 1e-06;
const double pi = acos(-1);
const int maxp = 1e5+10;

int sgn(double x){
    if(fabs(x) < eps) return 0;
    if(x < 0)return -1;
    else return 1;
}

inline double sqr(double x){return x*x;}

struct Point{
    double x,y;
    Point(){}
    Point(double _x,double _y){x = _x,y = _y;}
    void input(){scanf("%lf%lf",&x,&y);}
    void output(){printf("%.2f %.2f\n",x,y);}
    bool operator == (Point b)const{return sgn(x-b.x) == 0 && sgn(y-b.y) == 0;}
    bool operator < (Point b)const{return sgn(x-b.x) == 0 ? sgn(y-b.y)<0 : x<b.x;}
    Point operator -(const Point &b)const{return Point(x-b.x,y-b.y);}
    double operator ^ (const Point &b)const{return x*b.y-y*b.x;}    //叉积
    double operator * (const Point &b)const{return x*b.x+y*b.y;}    //点积
    Point operator + (const Point &b)const{return Point(x+b.x,y+b.y);}//
    Point operator * (const double &k)const{return Point(x*k,y*k);} //
    Point operator / (const double &k)const{return Point(x/k,y/k);} //
    double rad(Point a,Point b){Point p = *this;return fabs(atan2(fabs((a-p)^(b-p)),(a-p)*(b-p)));} //计算该点看a,b点的角度
    
};

struct polygon{
    int n;
    Point p[maxp];
    void input(int _n){
        n = _n;
        for(int i = 0; i < n; ++i) p[i].input();
    }
    struct cmp{
        Point p;
        cmp(const Point &p0){p = p0;}
        bool operator()(const Point &aa,const Point &bb){
            Point a = aa,b = bb;
            int d = sgn((a-p)^(b-p));
            if(d == 0) return sgn(a.distance(p)-b.distance(p))<0;
            return d > 0;
        }
    };
    void norm(){                                     //进行极角排序，首先找到最左下角的点
        Point mi = p[0];
        for(int i = 1; i < n; ++i) mi = min(mi,p[i]);
        sort(p,p+n,cmp(mi));
    }
    //Graham法得到凸包
    void Graham(polygon &convex){
        norm();
        int &top = convex.n;
        top = 0;
        if(n == 1){
            top = 1;
            convex.p[0] = p[0];
            return ;
        }
        if(n == 2){
            top = 2;
            convex.p[0] = p[0];
            convex.p[1] = p[1];
            if(convex.p[0] == convex.p[1]) top--;
            return ;
        }
        convex.p[0] = p[0];
        convex.p[1] = p[1];
        top = 2;
        for(int i = 2; i < n; ++i){
            while(top > 1 && sgn((convex.p[top-1]-convex.p[top-2])^(p[i]-convex.p[top-2])) <= 0) top--;
            convex.p[top++] = p[i];
        }
        if(convex.n == 2 && (convex.p[0] == convex.p[1])) convex.n--;
    }

};


int main() {
    int t,ca=1;
    cin>>t;
    while(t--){
        int n;
        polygon po,convex;
        cin>>n;
        po.input(n);
        if(n < 3){
            printf("Case %d: 0\n",ca++);
            continue;
        }
        po.norm();
        po.Graham(convex);
        if(convex.n == 2){
            printf("Case %d: 0\n",ca++);
            continue;
        }
        double minn = INF;
        for(int i = 1; i < convex.n-1; ++i){
            minn = MIN(minn,convex.p[i].rad(convex.p[i-1],convex.p[i+1])*180/pi);
        }
        minn = MIN(minn,convex.p[0].rad(convex.p[1],convex.p[convex.n-1])*180/pi);
        minn = MIN(minn,convex.p[convex.n-1].rad(convex.p[convex.n-2],convex.p[0])*180/pi);
        printf("Case %d: %lf\n",ca++,minn);
    }
    return 0;
}

/*

*/