采用状态空间法求解八数码问题

1. 问题描述

  八数码难题也称九宫问题，它是在3×3的方格棋盘上，分别放置了表有数字1、2、3、4、5、6、7、8的八张牌，初始状态$S_0$，目标状态$S_g$，要求程序能输入任意的初始状态和目标状态，通过空格来移动八张牌使得棋盘由初始状态到达目标状态。移动规则为：每次只能将与空格（上下左右）相邻的一个数字平移到空格中。

2. 算法思路

2.1 判断是否有解

  给定任意符合条件的初始状态$S_0$和目标状态$S_g$，并不一定存在解路线使得将初始状态转化为目标状态。因此，在求解前需要判断是否有解。
  八数码问题的一个状态实际上是0~9的一个排列，空格用0表示，对于任意给定的初始状态和目标状态，不一定有解，也就是说从初始状态不一定能到达目标状态。因为排列有奇排列和偶排列两类，排列只能在同类排列之间转化，而从奇排列不能转化成偶排列或相反。
  如果一个数字0~8的随机排列871526340，用$F(X)$表示数字$X$前面比它小的数的个数，全部数字的$F(X)$之和为$Y=\sum (F(X))$，如果$Y$为奇数则称原数字的排列是奇排列，如果$Y$为偶数则称原数字的排列是偶排列。
  例如：871526340这个排列的Y=0+0+0+1+1+3+2+3+0=10，10是偶数，所以是偶排列。871625340，Y=0+0+0+1+1+2+2+3+0=9，9是奇数，所以是奇排列。
  因此，可以在运行程序前检查初始状态和目标状态的排列是否相同，相同则问题可解，接着采用搜索算法求解，否则无解。

2.2 广度优先搜索求解

  我们定义结点$node$ ，搜索中每次出现的一个棋盘都相当于一个结点$node$，我们定义一个队列$queue$用于保存搜索中所出现的所有棋盘结点，一个棋盘结点为队列的一个成员。
  广度优先搜索的基本思想是：
  从初始结点$h$开始， 逐层地对结点进行扩展并考察它是否为目标结点，若不是目标结点，则放入待考察队列中；在第 n 层的结点没有全部扩展并考察之前，不对第 n+1 层的结点进行扩展。队列中的结点总是按进入的先后顺序排列，先进入的结点排在前面，后进入的排在后面。其搜索过程如图1所示。

图1 广度优先搜索过程

2.3 去重

  在搜索过程中，可能会同一状态重复搜索，有很多重复状态节点的扩展，会浪费时间。为解决这一问题使用哈希$map$，$map$键值为已经扩展过的状态节点编码后的字符串。当需要扩展状态节点$i$时，若$i$已经在$map$中，即已经扩展过，就不再扩展，否则对其进行扩展，并将$i$加入到$map$中。这里的哈希$map$使用C++ STL中的$unordered\_map$实现。

2.4 输出解路线

  每个节点保存其父节点，该节点由其父节点扩展而来，当搜索到目标状态时，根据父节点信息回溯回去，得到由初始状态到目标状态的解路线。

3. 数据结构及函数说明

3.1 数据结构

struct node {
	int a[3][3]; //九宫格 
	node* p;  //指向当前节点的父节点  
	node* next; //指向队列中下一个节点 
	node(string s) {
		for(int i=0;i<len;i++) {
			for(int j=0;j<len;j++) a[i][j] = s[i*len+j]-'0';
		}
		p = NULL;
		next = NULL;
	}
	node():p(NULL), next(NULL) {}
};

  定义一个结构体node表示广度优先搜索中的一个状态节点，其中：a是3*3二维数组，用来表示九宫格中每个位置的数字；p是指针，用来指向当前节点的父节点，这里的父节点是指当前节点由其父节点扩展而来；next是指针，指向广度搜索算法队列中的下一个节点；两个构造函数，分别用于有参数和无参数时结构体的初始化。

3.2 函数说明

3.2.1 input

  void input(node& start, node& target)，键盘输入八数码初始状态和目标状态。

3.2.2 haveSolution

  bool haveSolution(node start, node target)，判断输入的初始状态和目标状态是否有解，若有解返回true，否则返回false。

3.2.3 deCode

  string deCode(node t)，将node t中的八数码进行编码变成字符串，并返回编码后的字符串。

3.2.4 explore

  bool explore(node cur, node& ex, char dic)，该函数实现对cur状态节点进行指定方向的扩展，并通过ex参数将扩展后的结果返回，dic取值有“u,d,l,r”，分别表示空格向上、下、左、右移。若扩展成功返回true，否则返回false。

3.2.5 getSolution

  node* getSolution(node* start, node* target)，输入参数为指向初始状态节点的指针和指向目标状态节点的指针；该函数计算出一条从初始状态转化为目标状态的一条路线，并返回指向该路线最后一个节点的指针。

3.2.6 print

  void print(node* t)，输入参数t即为getSolution得到的指向结果路线最后一个节点的指针，print函数输出完整路线。

4. 流程图

  程序总体流程图如图2所示。

图2 程序总体流程图

5. C++代码

#include <bits/stdc++.h>
#include <string>
#define len 3
using namespace std;

struct node {
	int a[3][3]; //九宫格 
	node* p;  //指向当前节点的父节点  
	node* next; //指向队列中下一个节点 
	node(string s) {
		for(int i=0;i<len;i++) {
			for(int j=0;j<len;j++) a[i][j] = s[i*len+j]-'0';
		}
		p = NULL;
		next = NULL;
	}
	node():p(NULL), next(NULL) {}
};

void input(node& start, node& target);
bool haveSolution(node start, node target);
string deCode(node t);
bool explore(node cur, node& ex, char dic);
node* getSolution(node* start, node* target);
void print(node* t);

int main() {
	node start, target;
	input(start, target);
	if(!haveSolution(start, target)) {
		cout<<"奇偶不同，无解!!!"<<endl;
		return 0;
	}
	node* t = getSolution(&start, &target);
	if(t == NULL) cout<<"无解!!!"<<endl;
	else print(t);
	system("pause");
	return 0;
} 

void input(node& start, node& target) {
	//输入任意合法的初始状态和目标状态
	cout<<"请输入八数码初始状态，以3*3矩阵形式输入，空格用0表示"<<endl; 
	for(int i=0;i<len;i++) {
		for(int j=0;j<len;j++) cin>>start.a[i][j];
	}
	cout<<"请输入八数码目标状态，要求同初始状态"<<endl; 
	for(int i=0;i<len;i++) {
		for(int j=0;j<len;j++) cin>>target.a[i][j];
	}
}

bool haveSolution(node start, node target) {
	//判断初始状态和目标状态是否同为奇排列或同为偶排列，即是否有解 
	string s = "", t = "";
	int sc = 0, tc = 0;
	for(int i=0;i<len;i++) {
		for(int j=0;j<len;j++) {
			s += start.a[i][j]+'0';
			t += target.a[i][j]+'0';
		}
	}
	for(int i=1;i<s.length();i++) {
		for(int j=0;j<i;j++) {
			if(s[j]<s[i] && s[i]!='0' && s[j]!='0') sc++;
			if(t[j]<t[i] && t[i]!='0' && t[j]!='0') tc++;
		}
	}
	if(sc%2 == tc%2) return true;
	else return false;
}

string deCode(node t) {
	//将九宫格中的数字编码为字符串 
	string r = "";
	for(int i=0;i<len;i++) {
		for(int j=0;j<len;j++) r += t.a[i][j]+'0';
	}
	return r;
}

bool explore(node cur, node& ex, char dic) {
	//对当前状态cur进行扩展，dic为'u'表示空格向上移，'d'表示空格向下移
	//'l'表示向左移，'r'表示向右移，若无法扩展，返回false，若扩展成功，返回true，
	//并通过ex参数返回扩展后的节点 
	int r = 0, c = 0;
	for(int i=0;i<len;i++) {
		for(int j=0;j<len;j++) {
			if(cur.a[i][j] == 0) {
				r = i;
				c = j;
				break;
			}
		}
	}
	if(dic == 'u') {
		if(r == 0) return false;
		else swap(ex.a[r][c], ex.a[r-1][c]);
	}
	else if(dic == 'd') {
		if(r == len-1) return false;
		else swap(ex.a[r][c], ex.a[r+1][c]);
	}
	else if(dic == 'l') {
		if(c == 0) return false;
		else swap(ex.a[r][c], ex.a[r][c-1]);
	}
	else {
		if(c == len-1) return false;
		else swap(ex.a[r][c], ex.a[r][c+1]);
	}
	return true;
}

node* getSolution(node* start, node* target) {
	unordered_map<string,bool> m;
	node *front = start, *rear = front;
	string tarCode = deCode(*target);
	while(front!=NULL) {
		string curCode = deCode(*front);
		if(curCode == tarCode) {
			//找到目标状态 
			return front;
		}
		else {
			if(m.find(curCode)==m.end()) {
				//当前状态还未扩展过，进行扩展
				m[curCode] = true;
				node* dic[4];
				char op[4] = {'u','d','l','r'};
				for(int i=0;i<4;i++) dic[i] = new node(curCode);
				for(int i=0;i<4;i++) {
					if(explore(*front, *dic[i], op[i])) {
						dic[i]->p = front;
						rear->next = dic[i];
						rear = rear->next;
					}
				}
			}
		}
		front = front->next;
	}
	return NULL;
}

void print(node* t) {
	stack<node> s;
	while(t!=NULL) {
		s.push(*t);
		t = t->p;
	}
	cout<<endl<<"转化路线"<<endl;
	while(!s.empty()) {
		node cur = s.top();
		s.pop();
		for(int i=0;i<len;i++) {
			for(int j=0;j<len;j++) cout<<cur.a[i][j]<<" ";
			cout<<endl;
		}
		cout<<endl;
	}
}

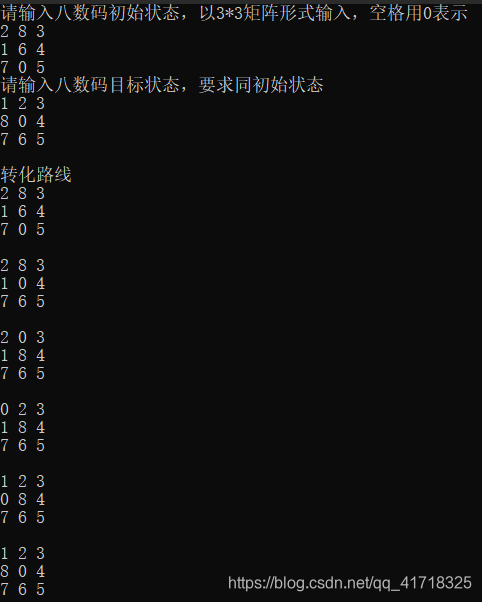
6. 代码运行结果

  代码运行结果如图3所示。

图3 代码运行结果