堆排序（完全二叉树用，利用完全二叉树的性质用数组存储）

最新推荐文章于 2025-05-29 11:22:53 发布

qq_41698081

最新推荐文章于 2025-05-29 11:22:53 发布

阅读量1k

点赞数 1

CC 4.0 BY-SA版权

分类专栏：算法模板

本文链接：https://blog.youkuaiyun.com/qq_41698081/article/details/89681594

算法模板专栏收录该内容

8 篇文章

订阅专栏

本文详细介绍了如何使用C++实现大顶堆的构建过程，并通过heapify和buildHeap函数确保完全二叉树满足堆的性质。进一步，通过heapSort函数实现了基于大顶堆的排序算法，该算法首先构建大顶堆，然后反复将堆顶元素与末尾元素交换并调整堆，直至完成排序。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

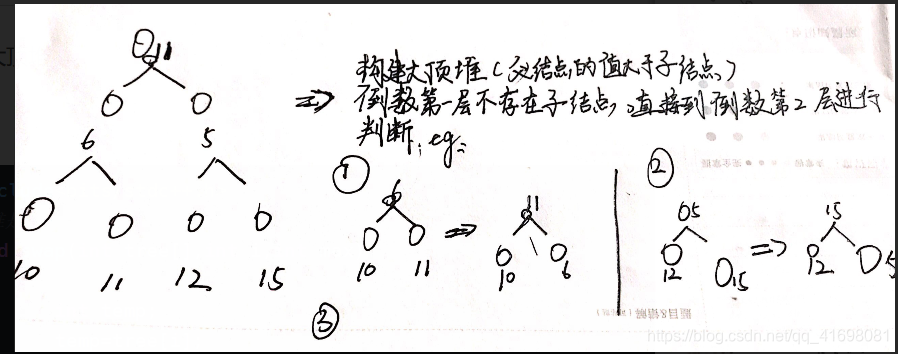
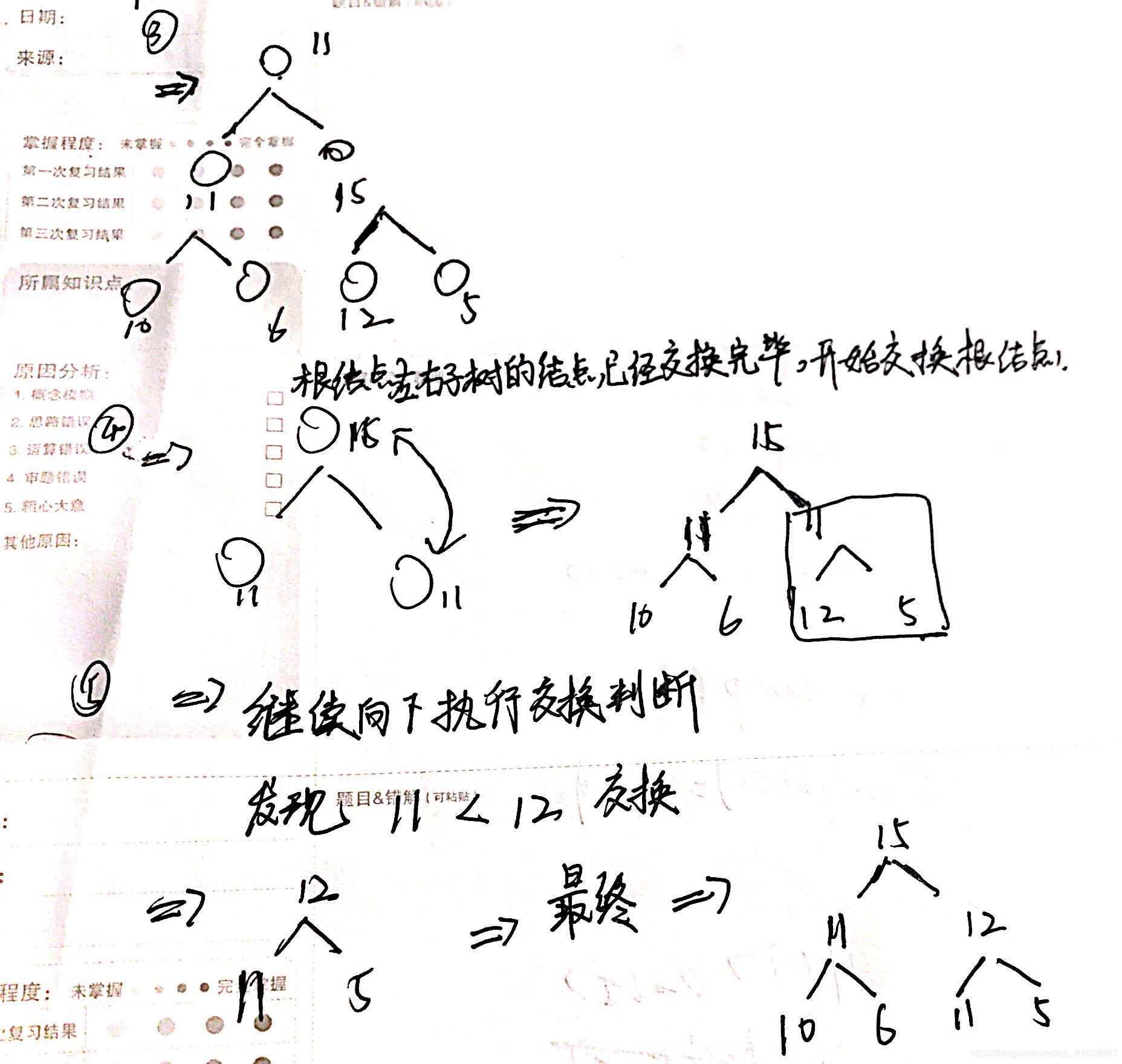
构建大顶堆：

#include<bits/stdc++.h> 
//堆是完全二叉树 
void swap(int tree[],int i,int max) //存在更大的结点值 （使此时最大结点的值与当前最大结点的值交换
{
	int temp;
	temp=tree[i];
	tree[i]=tree[max];
	tree[max]=temp;		
}
void heapify(int tree[],int n,int i){  //构建堆 buildHeap和heapify分开写更加灵活 
	if(i>=n){
		return;
	}
	int c1=2*i+1;
	int c2=2*i+2;
	int max=i;
	if(c1<n&&tree[max]<tree[c1]){
		max=c1; //这里的max为最大值的下标（索引位置）
	}
	if(c2<n&&tree[max]<tree[c2]){
		max=c2; //这里的max为最大值的下标
	}
	if(max!=i){     
		swap(tree,i,max); //交换结点tree[i], tree[max]
		heapify(tree,n,max);//交换了结点后， 左右子树被交换结点的子树需要重新构建堆
	}
	
}
void buildHeap(int tree[],int n){ // 	从最后一个元素构建堆 传入的n是tree数组中的最后一个元素为了保证
	int lastnode=n-1;				 //保证每个子结点的树都是堆 
	int parentId=(lastnode-1)/2;         //从最后一个不是叶节点的点开始往前做heapify操作的 
	for(int i=parentId;i>=0;i--){
		heapify(tree,n,i);
	}
}

void heapSort(int tree[],int n){//完成堆排序 
	buildHeap(tree,n);//此时使树中子结点都满足堆排序 
	for(int i=n-1;i>=0;i--){
		swap(tree,0,i);   
		heapify(tree,i,0);//重新构成堆，因为除了首节点外，其余的点
						  //都已经是堆结构了，所以不用buildHeap倒叙重新构建堆了 
	}
}
int main(){
	int tree[]={4,10,3,5,1,2};
	int n=6;
//	buildHeap(tree,6);
	heapSort(tree,n);
	for(int i=0;i<n;i++)   //此时是树中子结点都满足子堆 						   //但是不规则的堆就不能用 
		printf("%d\n",tree[i]);	
	
	return 0;
}