代码随想录-回溯算法

已于 2024-03-19 17:15:35 修改
阅读量515 收藏
点赞数 3
分类专栏： 刷题 文章标签： 算法 python 开发语言
于 2024-03-01 17:41:38 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_41638851/article/details/136402625
版权
文章介绍了回溯法在组合、排列问题中的应用，如组合问题、排列问题、子集、全排列等，包括基本模板、终止条件、剪枝优化技巧，以及示例代码，展示了如何使用回溯法寻找解决方案。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

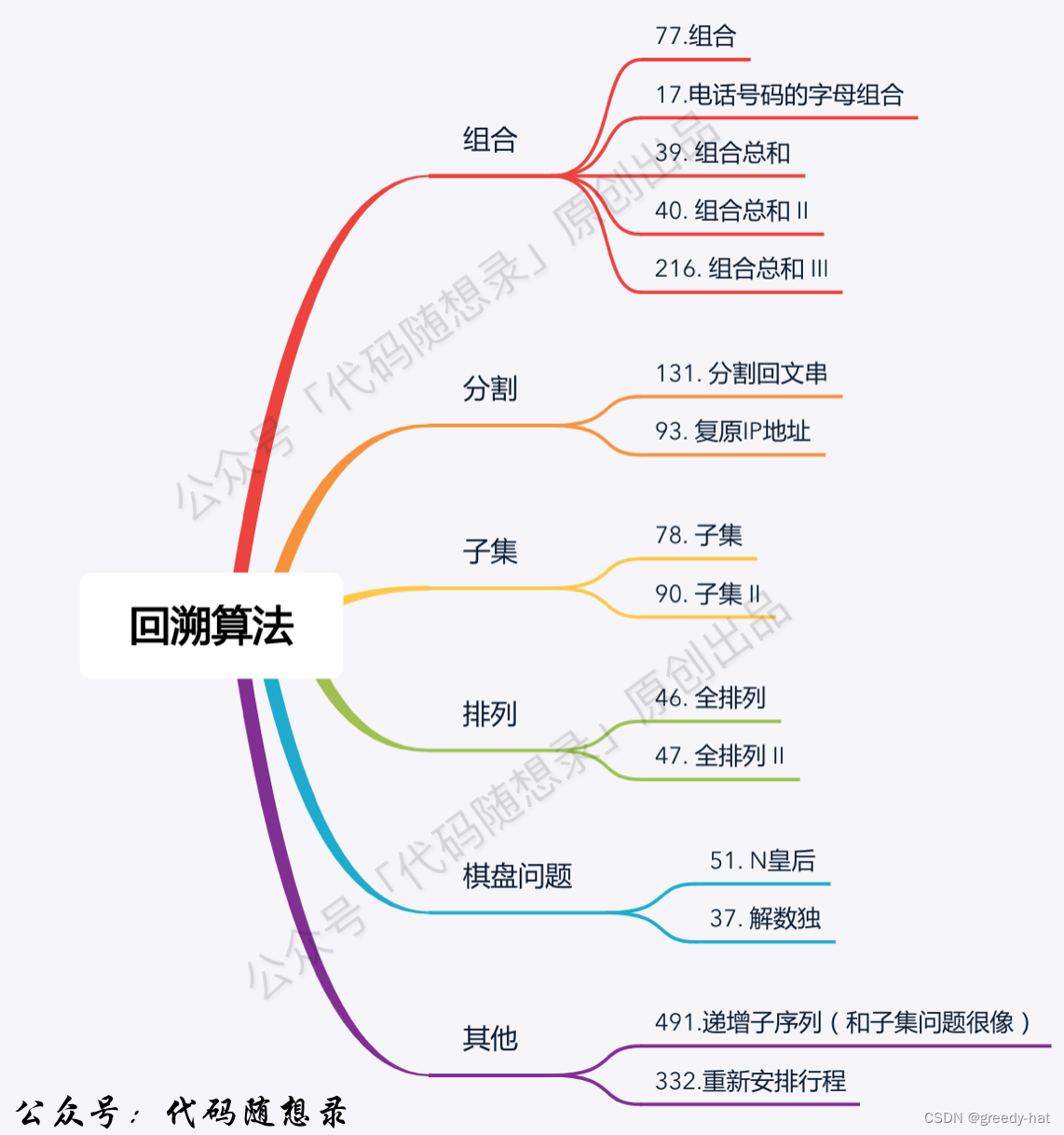
在这里插入图片描述
回溯法，一般可以解决如下几种问题：

  1. 组合问题：N个数里面按一定规则找出k个数的集合
  2. 切割问题：一个字符串按一定规则有几种切割方式
  3. 子集问题：一个N个数的集合里有多少符合条件的子集
  4. 排列问题：N个数按一定规则全排列，有几种排列方式
  5. 棋盘问题：N皇后，解数独等等

组合是不强调元素顺序的，排列是强调元素顺序。

回溯法模板
回溯三部曲

  1. 回溯函数模板返回值以及参数
void backtracking(参数)
  1. 回溯函数终止条件
if (终止条件) {
    存放结果;
    return;
}
  1. 回溯搜索的遍历过程
    在这里插入图片描述
    回溯函数遍历过程伪代码如下：
for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
    处理节点;
    backtracking(路径，选择列表); // 递归
    回溯，撤销处理结果
}

大家可以从图中看出for循环可以理解是横向遍历，backtracking（递归）就是纵向遍历，这样就把这棵树全遍历完了，一般来说，搜索叶子节点就是找的其中一个结果了。

分析完过程，回溯算法模板框架如下：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

6.组合

//未剪枝
class Solution {
    List<List<Integer>> ans = new ArrayList<>();
    Deque<Integer> path = new LinkedList<>();

    public List<List<Integer>> combine(int n, int k) {
        backtracking(n, k, 1);
        return ans;
    }

    public void backtracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            ans.add(new ArrayList<>(path));
            return;
        }
        for (int i = startIndex; i <= n; i++) {
            path.add(i);
            backtracking(n, k, i + 1);
            path.removeLast();
        }
    }
}

//剪枝
class Solution {
    List<List<Integer>> ans = new ArrayList<>();
    Deque<Integer> path = new LinkedList<>();

    public List<List<Integer>> combine(int n, int k) {
        backtracking(n, k, 1);
        return ans;
    }

    public void backtracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            ans.add(new ArrayList<>(path));
            return;
        }
        for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) {
            path.add(i);
            backtracking(n, k, i + 1);
            path.removeLast();
        }
    }
}
  1. 组合总和 III
class Solution {
    List<List<Integer>> ans = new ArrayList<>();
    Deque<Integer> path = new LinkedList<>();

    public List<List<Integer>> combinationSum3(int k, int n) {
        backtracking(k, n, 0, 1);
        return ans;
    }

    public void backtracking(int k, int targetSum, int sum, int startIndex) {
        if (path.size() == k) {
            if (sum == targetSum) {
                ans.add(new ArrayList<>(path));
            }
            return;
        }
        for (int i = startIndex; i <= 9; i++) {
            sum += i;
            path.add(i);
            backtracking(k, targetSum, sum, i + 1);
            sum -= i;
            path.removeLast();
        }
    }
}
  1. 电话号码的字母组合
class Solution {
    List<String> ans = new ArrayList<>();

    StringBuilder temp = new StringBuilder();

    public List<String> letterCombinations(String digits) {
        if (digits == null || digits.length() == 0) {
            return ans;
        }
        String[] numString = { "", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz" };
        backTracking(digits, numString, 0);
        return ans;
    }

    public void backTracking(String digits, String[] numString, int len) {
        if (len == digits.length()) {
            ans.add(temp.toString());
            return;
        }
        String str = numString[digits.charAt(len) - '0'];
        for (int i = 0; i < str.length(); i++) {
            temp.append(str.charAt(i));
            backTracking(digits, numString, len + 1);
            temp.deleteCharAt(temp.length() - 1);
        }
    }
}
  1. 组合总和
//未剪枝
class Solution {
    List<List<Integer>> ans = new ArrayList<>();
    Deque<Integer> path = new LinkedList<>();

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        bacaktracking(candidates, target, 0, 0);
        return ans;
    }

    public void bacaktracking(int[] candidates, int target, int sum, int startIndex) {
        if (sum > target) {
            return;
        }
        if (sum == target) {
            ans.add(new ArrayList<>(path));
            return;
        }
        for (int i = startIndex; i < candidates.length; i++) {
            sum += candidates[i];
            path.add(candidates[i]);
            bacaktracking(candidates, target, sum, i);
            sum -= candidates[i];
            path.removeLast();
        }
    }
}

在求和问题中，排序之后加剪枝是常见的套路！

//剪枝
class Solution {
    List<List<Integer>> ans = new ArrayList<>();
    Deque<Integer> path = new LinkedList<>();

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);
        bacaktracking(candidates, target, 0, 0);
        return ans;
    }

    public void bacaktracking(int[] candidates, int target, int sum, int startIndex) {
        if (sum == target) {
            ans.add(new ArrayList<>(path));
            return;
        }
        for (int i = startIndex; i < candidates.length; i++) {
            sum += candidates[i];
            if (sum > target) {
                break;
            }
            path.add(candidates[i]);
            bacaktracking(candidates, target, sum, i);
            sum -= candidates[i];
            path.removeLast();
        }
    }
}
  1. 组合总和 II
class Solution {
    List<List<Integer>> ans = new ArrayList<>();
    Deque<Integer> path = new LinkedList<>();

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);
        backtracking(candidates, target, 0, 0);
        return ans;
    }

    public void backtracking(int[] candidates, int target, int sum, int startIndex) {
        if (sum == target) {
            ans.add(new ArrayList<>(path));
            return;
        }
        for (int i = startIndex; i < candidates.length; i++) {
            if (i > startIndex && candidates[i] == candidates[i - 1]) {
                continue;
            }
            sum += candidates[i];
            if (sum > target) {
                break;
            }
            path.add(candidates[i]);
            backtracking(candidates, target, sum, i + 1);
            sum -= candidates[i];
            path.removeLast();
        }
    }
}
  1. 分割回文串
class Solution {
    List<List<String>> ans = new ArrayList<>();
    Deque<String> path = new LinkedList<>();

    public List<List<String>> partition(String s) {
        backtracking(s, 0);
        return ans;
    }

    public void backtracking(String s, int startIndex) {
        if (startIndex >= s.length()) {
            ans.add(new ArrayList<>(path));
            return;
        }
        for (int i = startIndex; i < s.length(); i++) {
            if (isPalindrome(s, startIndex, i)) {
                String str = s.substring(startIndex, i + 1);
                path.add(str);
            } else {
                continue;
            }
            backtracking(s, i + 1);
            path.removeLast();
        }
    }

    public boolean isPalindrome(String s, int start, int end) {
        for (int i = startIndex, j = end; i < j; i++, j--) {
            if (s.charAt(i) != s.charAt(j)) {
                return false;
            }
        }
        return true;
    }
}

93. 复原 IP 地址

class Solution {
    List<String> ans = new ArrayList<>();
    StringBuilder currentIP = new StringBuilder();

    public List<String> restoreIpAddresses(String s) {
        if (s.length() > 12)
            return ans;
        backtracking(s, 0, 0);
        return ans;
    }

    private void backtracking(String s, int startIndex, int pointNum) {
        if (pointNum == 3) {
            if (isValid(s, startIndex, s.length() - 1)) {
                currentIP.append(s.substring(startIndex));
                ans.add(currentIP.toString());
            }
            return;
        }
        for (int i = startIndex; i < s.length(); i++) {
            if (isValid(s, startIndex, i)) {
            	// 用于回溯
                int len = currentIP.length();
                currentIP.append(s.substring(startIndex, i + 1));
                if (pointNum < 3) {
                    currentIP.append(".");
                }
                backtracking(s, i + 1, pointNum + 1);
                // 回滚
                currentIP.setLength(len);
            } else {
                break;
            }
        }
    }

    private Boolean isValid(String s, int start, int end) {
        if (start > end) {
            return false;
        }
        if (s.charAt(start) == '0' && start != end) { // 0开头的数字不合法
            return false;
        }
        int num = 0;
        for (int i = start; i <= end; i++) {
            if (s.charAt(i) > '9' || s.charAt(i) < '0') { // 遇到非数字字符不合法
                return false;
            }
            num = num * 10 + (s.charAt(i) - '0');
            if (num > 255) { // 如果大于255了不合法
                return false;
            }
        }
        return true;
    }
}

class Solution {
    List<String> ans = new ArrayList<>();
    StringBuilder currentIP = new StringBuilder();

    public List<String> restoreIpAddresses(String s) {
        if (s.length() > 12)
            return ans;
        backtracking(s, 0, 0);
        return ans;
    }

    private void backtracking(String s, int startIndex, int pointNum) {
        if (pointNum == 3) {
            if (isValid(s, startIndex, s.length() - 1)) {
                currentIP.append(s.substring(startIndex));
                ans.add(currentIP.toString());

            }
            return;
        }
        for (int i = startIndex; i < s.length(); i++) {
            if (isValid(s, startIndex, i)) {
                int len = currentIP.length();
                currentIP.append(s.substring(startIndex, i + 1));
                if (pointNum < 3) {
                    currentIP.append(".");
                }
                backtracking(s, i + 1, pointNum + 1);
                currentIP.setLength(len);
            } else {
                break;
            }
        }
    }

    private Boolean isValid(String s, int start, int end) {
        if (start > end) {
            return false;
        }
        if (s.charAt(start) == '0' && start != end) {
            return false;
        }
        if (Integer.parseInt(s.substring(start, end + 1)) < 0 || Integer.parseInt(s.substring(start, end + 1)) > 255) {
            return false;
        }
        return true;
    }
}
  1. 子集
class Solution {
    List<List<Integer>> ans = new ArrayList<>();
    Deque<Integer> path = new LinkedList<>();

    public List<List<Integer>> subsets(int[] nums) {
        backtracking(nums, 0);
        return ans;
    }

    public void backtracking(int[] nums, int startIndex) {
        ans.add(new ArrayList<>(path));
        if (startIndex >= nums.length) {
            return;
        }
        for (int i = startIndex; i < nums.length; i++) {
            path.add(nums[i]);
            backtracking(nums, i + 1);
            path.removeLast();
        }
    }

}
  1. 子集 II
class Solution {
    List<List<Integer>> ans = new ArrayList<>();
    Deque<Integer> path = new LinkedList<>();

    public List<List<Integer>> subsetsWithDup(int[] nums) {
        Arrays.sort(nums);
        backtracking(nums, 0);
        return ans;
    }

    public void backtracking(int[] nums, int startIndex) {
        ans.add(new ArrayList<>(path));

        for (int i = startIndex; i < nums.length; i++) {
            if (i > startIndex && nums[i - 1] == nums[i]) {
                continue;
            }
            path.add(nums[i]);
            backtracking(nums, i + 1);
            path.removeLast();
        }
    }
}
  1. 非递减子序列
class Solution {
    List<List<Integer>> ans = new ArrayList<>();
    Deque<Integer> path = new LinkedList<>();

    public List<List<Integer>> findSubsequences(int[] nums) {
        backtacking(nums, 0);
        return ans;
    }

    public void backtacking(int[] nums, int startIndex) {
        if (path.size() >= 2) {
            ans.add(new ArrayList<>(path));
        }
        Set<Integer> set = new HashSet<>();
        for (int i = startIndex; i < nums.length; i++) {
            if (!path.isEmpty() && path.peekLast() > nums[i] || set.contains(nums[i])) {
                continue;
            }
            set.add(nums[i]);
            path.add(nums[i]);
            backtacking(nums, i + 1);
            path.removeLast();
        }
    }
}
  1. 全排列
class Solution {
    List<List<Integer>> ans = new ArrayList<>();
    Deque<Integer> path = new LinkedList<>();

    public List<List<Integer>> permute(int[] nums) {
        if (nums.length == 0) {
            return ans;
        }
        backtracking(nums, path);
        return ans;
    }

    public void backtracking(int[] nums, Deque<Integer> path) {
        if (path.size() == nums.length) {
            ans.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < nums.length; i++) {
            if (path.contains(nums[i])) {
                continue;
            }
            path.add(nums[i]);
            backtracking(nums, path);
            path.removeLast();
        }
    }
}
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值