Coursera学习笔记 Week 1

第一次在网上这样做笔记，有点不知道怎么下手了。刚发现优快云似乎不太适合数学公式的编辑，先试着把这周的内容串起来一下，之后再去试试有道云笔记。

• What is machine learning?

• 两个定义：

1、在特定编程下，赋予计算机学习能力的领域。（西洋棋算法的例子）

2、一个程序被认为能从经验E中学习，解决任务T，达到性能度量值P，当且仅当，有了经验E后，经过P评判，程序在处理T时的性能有所提升。

• 机器学习的分类：

• 监督学习：所给出的数据集有明确的输入输出关系，即所给的数据集已经给出了答案（标签），目的是基于此做出预测。

• 监督学习的分类：

1. 回归问题（regression）:预测一个准确值
2. 分类问题（classification）:预测一个离散值（比如0/1）

• 无监督学习：所给出的数据集只有一种，需要我们找出数据集中蕴含的类型结构。

• Model and cost founction

• Model representation（模型建立）：找到训练样本中适合作为输入变量（特征量）的X和输出变量（目标变量）的y建立函数模型。
• Cost Founction：通过找代价函数（使预测值和实际值之间的距离最小）的最小值来选择模型

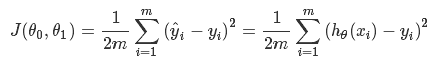
打不出公式只能截图先凑合一下了。

• 代价函数这里我觉得重点是它和假设函数的联系与区别，联系在于代价函数是为了确定假设函数中的参数，而区别在于代价函数的变量正好是假设函数的参数。

• Parameter learning

• Gradient Descent（梯度下降法，用来找到代价函数的局部最优解）

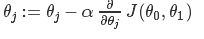
1. 梯度下降法中更新每一次的值时要做到同时更新（：=和=的区别： ：=表示赋值，=表示声明）
2. 导数项是用来控制下降的方向，并且随着到达最优解处会越来越小（接近局部最低点时自动减小幅度）
3. α的值太小会使下降速度太慢，太大会错过最优解
   

• Linear Algebra Review

• 矩阵和向量的基本概念
• 矩阵的加法和乘法
• 矩阵与矩阵相乘

• 矩阵乘法不满足交换律但满足结合律

• 矩阵的转置和逆

• 方阵才有逆矩阵。
• 奇异矩阵（退化矩阵）：没有逆矩阵的矩阵（元素都为0的矩阵）
• 没有逆矩阵的矩阵元素可近似认为都是0.