Reinforcement Learning - An Introduction强化学习读书笔记 Ch5.3-Ch5.7

5.3蒙特卡洛控制

采用蒙特卡洛解决控制问题，采用类似于DP算法中广义策略迭代的方式。
在策略迭代中，同时维护近似的策略和近似的价值函数，通过不断迭代逼近真实的价值函数，并且根据价值函数调优策略。
策略评估：采用与DP中完全相同的方法，只要每个状态动作都被经历了无数次，MC即可以收敛。
策略改进：采用贪心算法，每次选择当前状态下最大的动作价值函数。
可证明根据贪心法，总能每步都得到更优的策略，且最终总会找到最优策略：

基于试探性出发的MC方法如下:

5.4没有试探性出发假设的蒙特卡洛控制

on-policy
用于生成采样数据序列的策略和用于实际决策的待评估和改进的策略是相同的。
off-policy
用于生成采样数据序列的策略和用于实际决策的待评估和改进的策略是不同的。
在on-policy中，策略一般是软性的，确保每一个动作都被遍历到。为了达到这个目的，采用$ϵ-greedy$。
GPI流程中并不要求优化过程中遵循的策略一定是贪心的，只需要逼近于贪心策略即可，因此可以用$ϵ-greedy$来代替试探性出发。
on-policy的首次访问型MC算法如下：、

而这个算法能使得策略改进定理成立：

注意其中的第一个不等号成立，是因为加入的是一个加权平均项，而这个权重的和是为1的，那么做一个和为1的权重的加权平均的话，其期望一定小于等于其中的最大值，而这个权重项进一步拆分之后就能得到同类项合并而得到结果。

5.5基于重要度采样的off-policy策略

off-policy采用两个策略，一个用来生成样本，更有试探性，称为行动策略。一个用来生成最优策略，称为目标策略。
行为策略必须是完全已知的，并且能被目标策略覆盖。即目标策略所有可能采取到的行动，在行为策略中被选取的概率也必须大于0。
重要度采样：
使用行动策略的采样结果来对目标策略进行更新会产生误差，一次你可以用轨迹在目标策略与行动策略中出现的相对概率进行加权，这个相对比例称为重要度采样比，对应的公式为：

注意整体的轨迹概率值是与MDP中的状态转移概率有关的，并且这种动态特性通常是未知的，但是在分子分母中可以将其约掉，所以重要度采样的最终结果只与两个策略和样本序列有关，而与动态特性无关。
使用比例系数之后，可以调整行动策略对应的回报使其具有正确的期望值。
重要度采样方法分为普通版和加权版：

普通重要度采样方法，是无偏估计，但方差大。

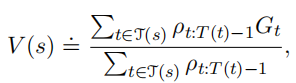
加权重要度采样方法，是有偏的，但是方差小，且在实践中进场能试的开始的错误率更低。

5.6增量式实现

与第二章的增量更新类似，为了减少记录量，可以使用增量式更新来实现更新：

对应的off-policy MC算法为：

5.7 off-policy蒙特卡洛控制

on-policy方法在对某个策略进行控制的同时，也对这个策略进行价值评估，但是在off-policy方法中这两个过程是分开的。
off-policy MC控制算法如下:

其中目标策略采用固定策略，行动策略采用软性策略。