机器学习之聚类算法

定义：将相似的事物进行归类，聚类分析又称为同质分组或者无监督分类，指把数据分成不同的簇，每簇中的数据相似而不同簇之间的数据距离较远

• 簇内文档之间应该彼此相似
• 簇内文档之间差异大

无监督意味着没有已标注好的数据集

分类和聚类的区别：

1. 分类：是有监督的学习，且类别事先人工定义好，并且是学习算法输入的一部分
2. 聚类：是无监督的学习，在没有人工输入的情况下从数据中推理而得

聚类的评价指标也是纯度，但这个纯度和决策树里面的纯度不同

对于每一个簇ω_k：找到一个类别C_j，该类别包含ω_k中的元素最多，为n_kj个，也就是说ω_k的元素最多分布在C_j中

将所有的n_kj求和，然后除以所有的文档数目

例：

所以，由此可推得，当完全分类正确的时候，其纯度为1，所以纯度越高，则分类越准确

聚类的要求：

• 将相关数据放到同一个簇中，将不同文档放到不同的簇中
• 簇的数目应该合适，一遍与聚类的数据集相吻合
• 假定给定簇的数目初始值为K
• 聚类时要注意避免非常小和非常大的簇
• 定义的簇要方便理解

聚类的算法：

1. 扁平算法
   • 通过一开始将全部或部分文档随机划分为不同的组
   • 通过迭代方式不断修正
   • 代表算法：K-均值聚类算法
2. 层次算法：
   • 构建具有层次结构的簇
   • 自底向上(Boottom-up)的算法称为凝聚式(agglomerative)算法
   • 自顶向下(Top-down)的算法称为分裂式(divisive)算法

扁平算法代表算法：K-Means算法

K：是聚类算法中类的个数

means：是均值算法

而K-Means算法是指用均值算法把数据分成K个类的算法

扁平算法步骤：

• 扁平算法将N篇文档划分为K个簇
• 给定一个文档集合及聚类结果簇的个数K
• 寻找一个划分这个文档集合分成K个簇，该结果满足某个最优划分准则

全局优化：穷举所有划分结果，从中选择最优的那个划分结果（不太可取，因为随着样本数量的增加，其计算量会呈指数式增长）

K-均值聚类算法为启发式算法（启发式算法是相对于最优化算法提出的，是基于直观或者经验构造的算法，在可接受的开销（时间和空间）内给出待解决组合优化问题的一个可行解。启发式算法还有模拟退火算法，蚁群算法，遗传算法，人工神经网络）

K-均值聚类算法中的每个簇都定义为其质心向量

K-均值聚类算法的划分准则：使得所有文档到其所在簇的质心向量的平方和最小

质心向量的定义：

ω代表一个簇

目标优化：

• 重分配(reassignment)：将每篇文档分配给离它最近的簇
• 重计算(recomputation):重新计算每个簇的质心相向量

K-均值聚类算法必定是收敛的

• 达到收敛所需时间未可知

• 如果不太关心少许文档在不同簇类之间的交叉（在一定误差范围内），收敛速度一般会很快

• 完全的收敛会需要非常多次的迭代过程才会收敛

• K-Means算法的损失函数是平方误差，如下所示：

  

K-Means算法的基本步骤：

• 首先随机选取k个数据点作为聚类中心
• 然后计算其他点到这些聚类中心点的距离，当某一个点距离其中一个聚类中心最近，则视为此点与这个聚类中心点为同一类
• 然后通过对簇中距离平均值的计算，不断改变这些聚类中心的位置（也就是不断迭代），直到这些聚类中心不再变化为止
• 注意，上面的计算步骤之前要视数据情况来对数据进行标准化（对不同特征维度的伸缩变换的目的是使得不同度量之间的特征具有可比性。同时不改变原始数据的分布）和归一化（对不同特征维度的伸缩变换的目的是使各个特征维度对目标函数的影响权重是一致的）

影响K-Means算法精度的决定因素：

• 数据的采集和抽象以及数据的初始的中心聚类点选取
• K值的大小
• 最大迭代次数与收敛值的选定
• 度量距离的手段

种子的随机选择只是K-Means算法的一种初始化方法，可以用一些更好的办法来确定初始质心向量：

• 非随机地采用某些启发式算法来选择种子（可以过滤掉一些离群点，或者寻找具有较好文档空间覆盖的种子集合）
• 采用层级聚类算法寻找更好的种子
• 选择i次不同的随机种子集合，对每次产生的随机种子集合巡行K-Means算法，最后选择具有最小RSS值的聚类结果

K值的取值：

• 在某些场景下，簇的个数K是事先给定的，也就是说存在外部约束
• 在未对K值有所限制的场景下，可以对其定义一个优化准则，例如可以给定一个文档，找到达到最优情况下的K值

连续值的相似度计算：

对于二值离散型的相似度计算

• 二值离散型属性只有0和1两个取值

• 假设两个样本X_i和X_j分别表示成如下形式：

  • X_i=(x_i1,x_i2x_i3,…,x_ip)

  • X_j=(x_j1,x_j2x_j3,…,x_jp)

    他们都是p维特征向量，并且每一维特征都是一个二值离散型数值

• 计算步骤如下所示：

其中，SMC和JC都是表示距离，其值越大表示相似度越差，如果对某一个属性的倾向没有主次之分，可以选择SMC，若对属性有所侧重，则选择JC

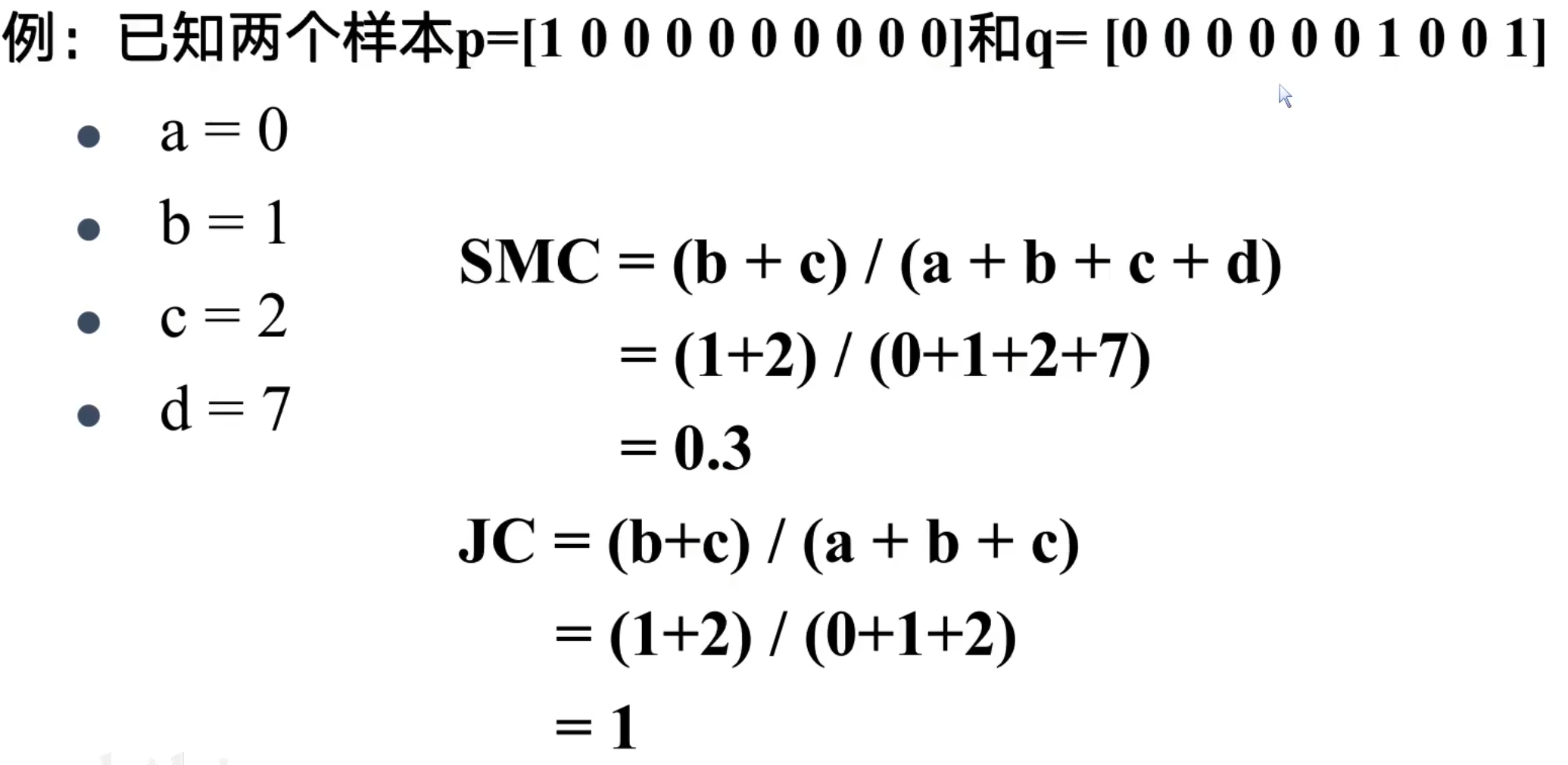
层次聚类算法

对给定的数据集进行层次分解：

• 自底向上方法（合并）：开始时，将每个样本作为单独的一个组；然后依次合并相近的样本或组，直至所有的样本或组被合并为一个组或者达到终止条件为止，代表算法:AGNES算法
• 自顶向上方法（分裂）：开始时，将所有样本置于一个簇中，然后，执行迭代，在迭代的每一步中，一个簇被分裂为多个更小的簇，直至每个样本分别在一个单独的簇中或者达到终止条件为止，代表算法：DIANA算法

合并的步骤是将两个最相似的簇进行合并，直到还剩一个簇或者到达终止条件，其详细步骤如下所示：

1. 将一开始的的每篇文档作为一个独立的簇
2. 然后将其中两个最相近的簇进行合并
3. 重复上一步直至仅剩一个簇
4. 整个合并步骤构成一个二叉树

在簇的合并过程中需要判断簇的相似度之后才能选择两个最接近的簇进行合并，所以，需要解决的关键问题为定义簇的相似度：

• 单连接：最大相似度（对离群点具有较好的判别）
  • 计算任意两篇文档之间的相似度，取其中的最大值
• 全连接：最小相似度（对离群点可能会产生误判）
  • 计算任意两篇文档之间的相似度，取其中的最小值
• 质心法：平均的类间相似度（相对较好）
  • 所有的簇间文档对之前相似度的平均值（不包括同一个簇内的文档之间的相似度）
  • 这等价于两个簇质心之间的相似度
• 组平均：平均的类内和类间相似度（相对较好）
  • 所有的簇间文档对之间相似度的平均值（包括同一个簇内的文档之间的相似度）
• 注意相似度和距离的关系，相似度越大，表示簇越接近，则距离越大
• 注意最大相似度和最短距离之间的关系，取最大相似度的时候也就是最接近的时候，此时的距离必然最短

如下图所示：