一、特征工程

二、数据清洗:
1、数据样本抽样
2、异常值(空值)处理





在特征预处理的过程中,进行数据标注是非常重要的,比如我们想要预测明天下雨不下雨,那么这个时候我们得到的数据中,需要对关于我们预测的结果的数据进行标注,也就是下雨不下雨进行标注。

上图是一个hr的人力资源的分析图,我们用这个数据会去预测员工是否离职。 并且建立模型,得出什么样的人会离职。
而我们的labe标注在left上面。属性为1为离职,属性为0代表不离职。



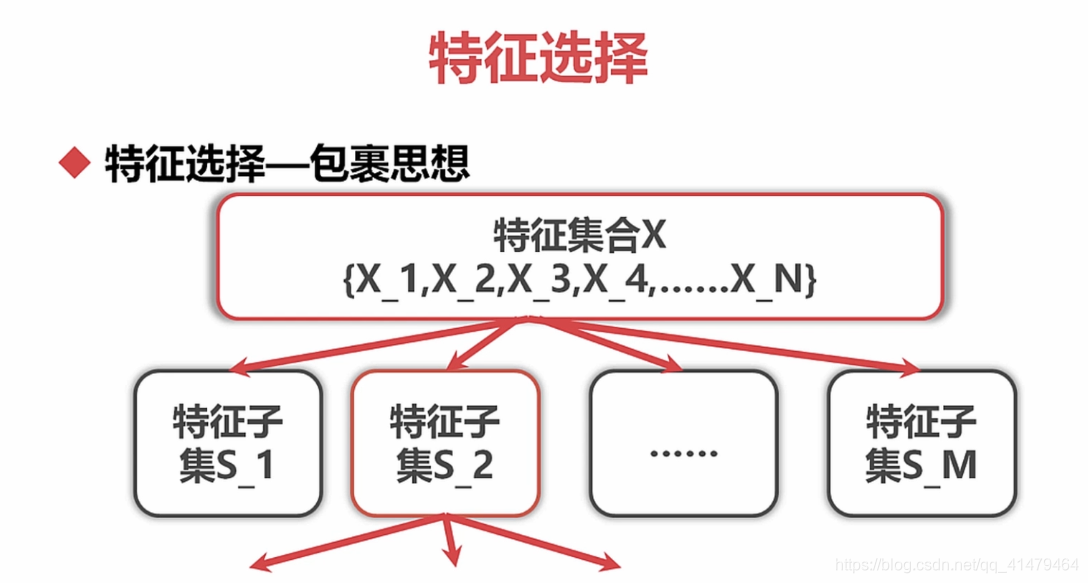


特征变换:对指化,就是对特征进行对数化和指数化。

先对特征进行指数化,然后再进行归一化(softmax)。
对特征进行对数化:

数据离散化:就是将连续数据变成离散数据的过程

- 方法就是分箱技术:等频分箱,等距分箱
- 朴素贝叶斯算法:需要的数据就是离散的
分箱技术:
根据深度和宽度对数据进行分箱

第一个是等深分箱,和等距分箱的实践
归一化是数据在[0,1]之间:
正规化:用在每个对象的各个特征的表示最多

用python操作正规化:

根据上面的公式得出的正规化的数据

注意下面的是 L1,L2的正规化。
from sklearn.preprocessing import Normalizer import numpy as np #正规化实际上是对行进行正规化的 x = Normalizer(norm="l1").fit_transform(np.array([1,1,3,-1,2]).reshape(-1,1)) print(x) b = Normalizer(norm="l2").fit_transform(np.array([[1,1,3,-1,2]])) print(b)
正规化的结果如下:

特征降维:



用python操作lda的实现过程
import numpy as np
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
X = np.array([[-1,-1],[-2,-1],[-3,-2],[1,1],[2,1],[3,2]])
Y = np.array([1,1,1,2,2,2])
m_lda = LinearDiscriminantAnalysis(n_components=1).fit_transform(X,Y)
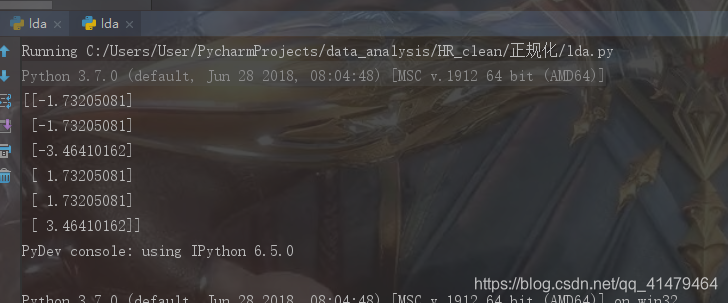
print(m_lda)lda实现结果:
























 1959
1959

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








