4-3 缩放 位移 旋转 矩阵

前言

1. 矩阵就是基底
2. 一般列向量都是有一个"单位基底"
3. 矩阵:缩放/位移/旋转-矩阵

4.上一章学习了单位矩阵 列向量

$$列向量=\left[\begin{array}{c}x\\ y\\ z\\ w-齐次坐标\end{array}\right]$$

$$单位矩阵=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$
单位矩阵可以理解为 基底,所有的向量都具有一个前置的 单位矩阵的基底

重要公式一:
v = 单位矩阵× v
v = 单位基底× v

一 、位移矩阵

基底改变后,向量v就改变了
S=Scaling Factor
$$Scale=\left[\begin{array}{cccc}Sx& 0& 0& 0\\ 0& Sy& 0& 0\\ 0& 0& Sz& 0\\ 0& 0& 0& 1\end{array}\right]$$
Sx Sy Sz 可以单独改变 x y z三个值,因为这三个值 (SxX,SyY, Sz*Z,1)T

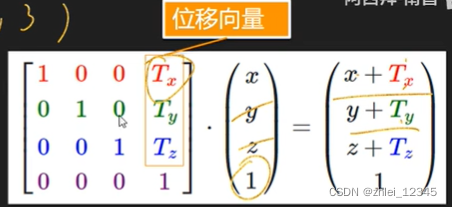
二、移动矩阵

1.本来移动每个坐标仅仅需要加法, 但是为了统一还是用乘法
2.齐次坐标 (列向量的最后一个),可以辅助用乘法解决移动.
3.如果齐次坐标w=0,那么这个向量不可以移动
4.齐次坐标决定是否可以移动.取值只要 0 1

T=Translation
$$位移矩阵=\left[\begin{array}{cccc}1& 0& 0& Tx\\ 0& 1& 0& Ty\\ 0& 0& 1& Tz\\ 0& 0& 0& 1\end{array}\right]$$

三、旋转矩阵

1.理解:把矩阵拆成三行
$$矩阵=\left[\begin{array}{cccc}Sx& 0& 0& Tx\\ 0& Sy& 0& Ty\\ 0& 0& Sz& Tz\\ 0& 0& 0& 1\end{array}\right]$$
这样就发现了,不影响的因素=行

$$影响x[第一行]=\left[\begin{array}{cccc}Sx& 0& 0& Tx\end{array}\right]$$
$$影响y[第二行]=\left[\begin{array}{cccc}0& Sy& 0& Ty\end{array}\right]$$

$$影响z[第三行]=\left[\begin{array}{cccc}0& 0& Sz& Tz\end{array}\right]$$

2. 理解旋转
   重要公式 二:
   绕着X轴旋转,则X值不能发生变化
   
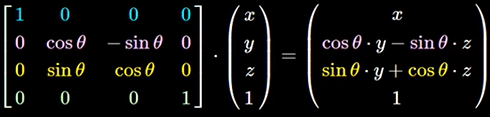
   也就是影响第一行的数字一定是
   $$影响x[第一行]=\left[\begin{array}{cccc}1(Sx)& 0& 0& 0(Tx)\end{array}\right]$$

3. 所有旋转公式

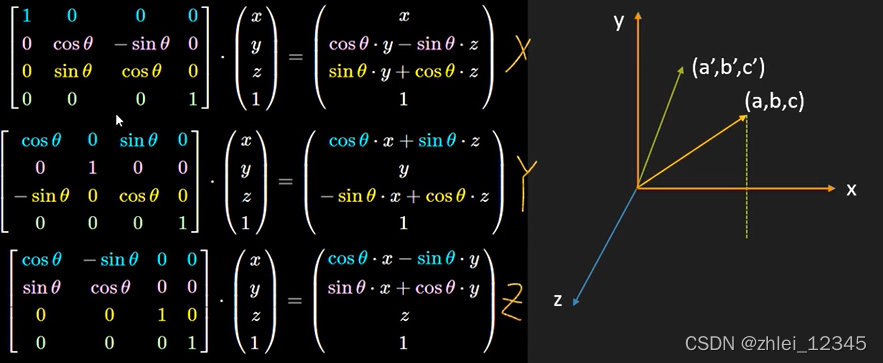
4. 推导公式
   4.1 旋转矩阵就是改变了标准向量的基底
   4.2 旋转矩阵描述的变幻 = 改变后的值,在原有的坐标系是多少
   
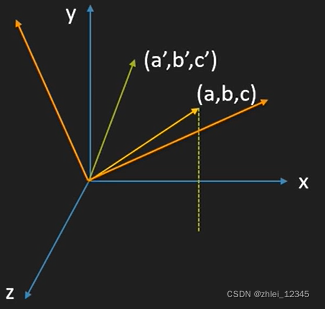
   影响旋转的因素=列
   
   cosθ, 表示新的长度 = 原有长度的cosθ
   sinθ,表示新的长度 = 原有长度的sinθ

四、矩阵的组合

顺序:先Scale 再Trans
以后应用:就是先scalc 再Trans