B树

B树在文件系统和数据库系统中使用较多，适用于组织 动态的索引结构。它不是二叉树，是一种多路平衡查找树，多路是指树的分支多于二叉；平衡是指所有叶子结点均在同一层上，以避免出现单支树的情况。
B树的阶：树中所有结点的孩子结点数的最大值，通常用m来表示，从查找效率来考虑通常取m>=3。

定义

一棵m阶的B 树（意味着某一个节点最多有m个字树，但这并不意味着m阶树就叫m叉树）。

1. 树中每个结点最多含有m个孩子（m>=2）；
2. 除根结点和叶子结点外，其它每个结点至少有[ceil(m / 2)]个孩子（其中ceil(x)是一个取上限的函数）；
3. 若根结点不是叶子结点，则至少有2个孩子（特殊情况：没有孩子的根结点，即根结点为叶子结点，整棵树只有一个根节点）；
4. 所有叶子结点都出现在同一层
5. 每个非终端结点中包含有n个关键字信息：(n，P0，K1，P1，K2，P2，…，Kn，Pn)。其中：

• a) Ki (i=1…n)为关键字，且关键字按顺序升序排序。
• b) Pi为指向子树根的接点，且指针P(i-1)指向子树种所有结点的关键字均小于Ki，但都大于K(i-1)。
• c) 关键字的个数n必须满足： [ceil(m / 2)-1]<= n <= m-1。

盗图一张

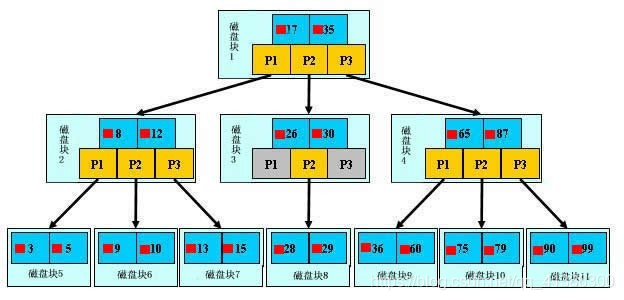
B树的查找

对于上图，查找数据29，过程：
1.找到磁盘块1，加载到内存中（IO一次）。
2.查到在磁盘块3上，加载磁盘块3到内存（IO一次）。
3.查到在磁盘块8上，加载到内存中（IO一次）。

待查关键字为key； 树中第i个关键字为ki
若key=ki，则查找成功；
若key<ki，则沿指针p，则沿指针pi-1所指的子树继续查找；
若ki<key<ki+1,则沿指针pi所指的子树继续查找；
若key>ki+1 则沿指针pi+1所指的子树继续查找；
若直至找到叶子结点且叶子结点中查找也不成功，则查找失败

B树的插入

举例：5阶的树，根据定义有下面两个规则：
定义1：树中每个结点最多含有5个孩子
定义5：每个非终端结点中包含[Ceil[(5/2)] - 1 , m-1] 个关键字，即关键字最多4个（因为还有一个结点存储的是关键字个数），最少2个。
例：假设插入的数据 是C N G A H E K Q M F W L T Z D P R X Y S

第一步：因为关键字最大是4个，所以前四个插入不会破坏规则，这里就直接插入4个数据C,N,G,A,。

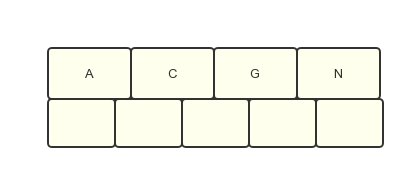
第2步 ：
2.1 当插入H时，发现次数关键字数量超过4个了，需要执行分裂的操作
插入前状态如下

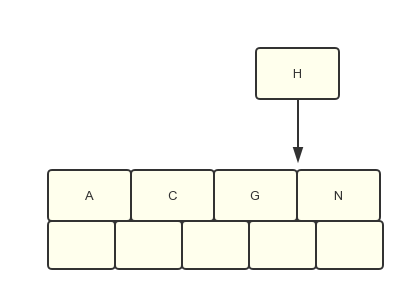
2.2 分裂过程如下：
2.2.1 生成一新结点。
2.2.2 把原结点上的关键字和H按升序排序后，从中间位置把关键字（不包括中间位置的关键字）分成两部分。左部分所含关键字放在旧结点中，右部分所含关键字放在新结点中，中间位置的关键字连同新结点的存储位置插入到父结点中。
2.2.3 如果父结点的关键字个数也超过（m-1），则要再分裂，再往上插。直至这个过程传到根结点为止。

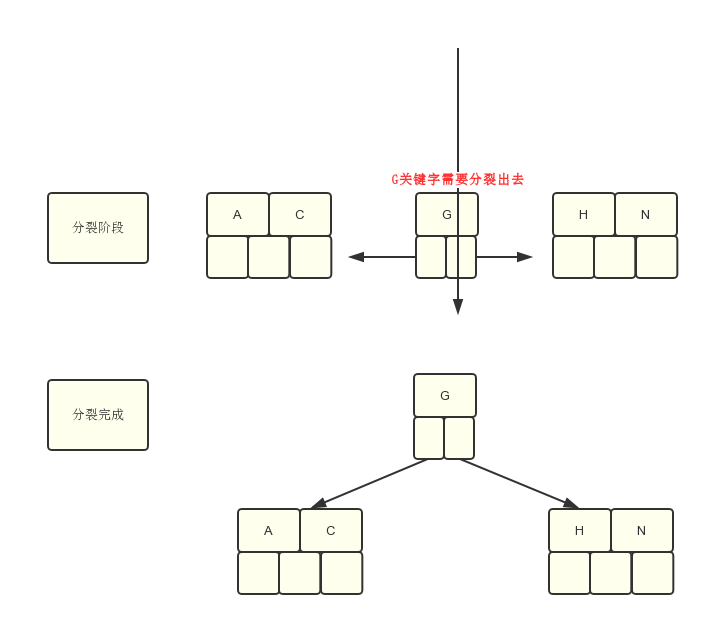
2.3 插入后状态如下:

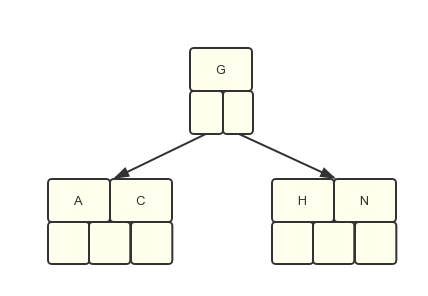
第3步：插入E，K，Q时不需要分裂

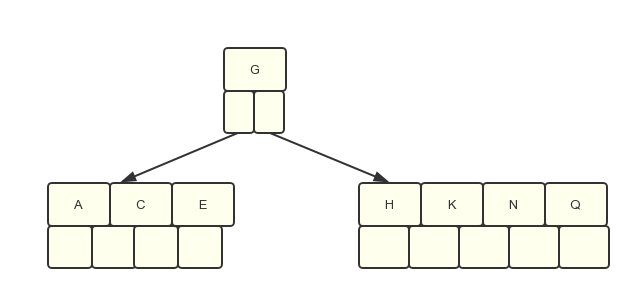
第4步：插入M时，需要分裂，因为关键字个数大于4了

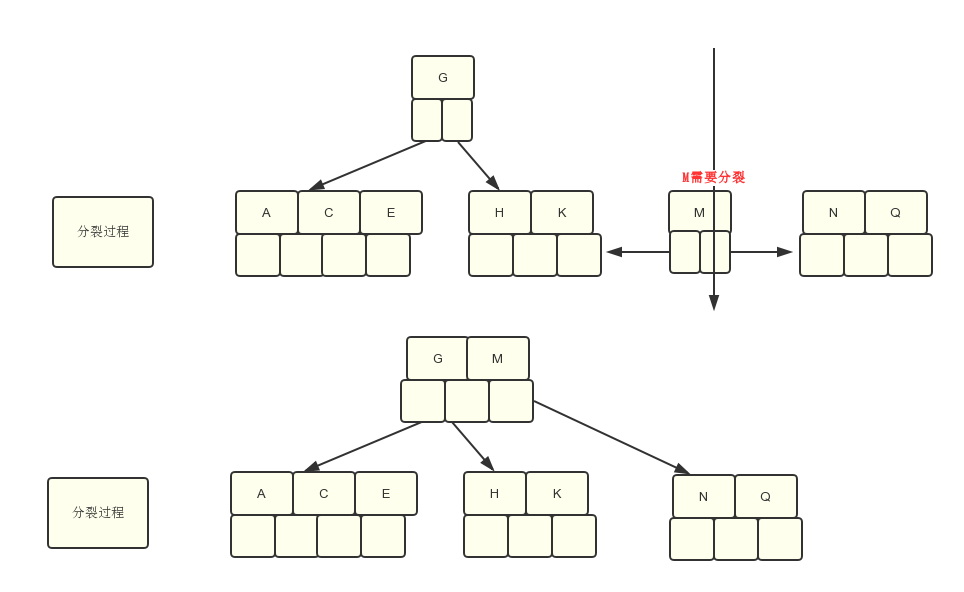
第5步：插入F,W,L,T不需要分裂操作

第6步：.插入Z时，最右边的需要分裂，这里就直接贴结果，不分析了，具体分析上面已经有了

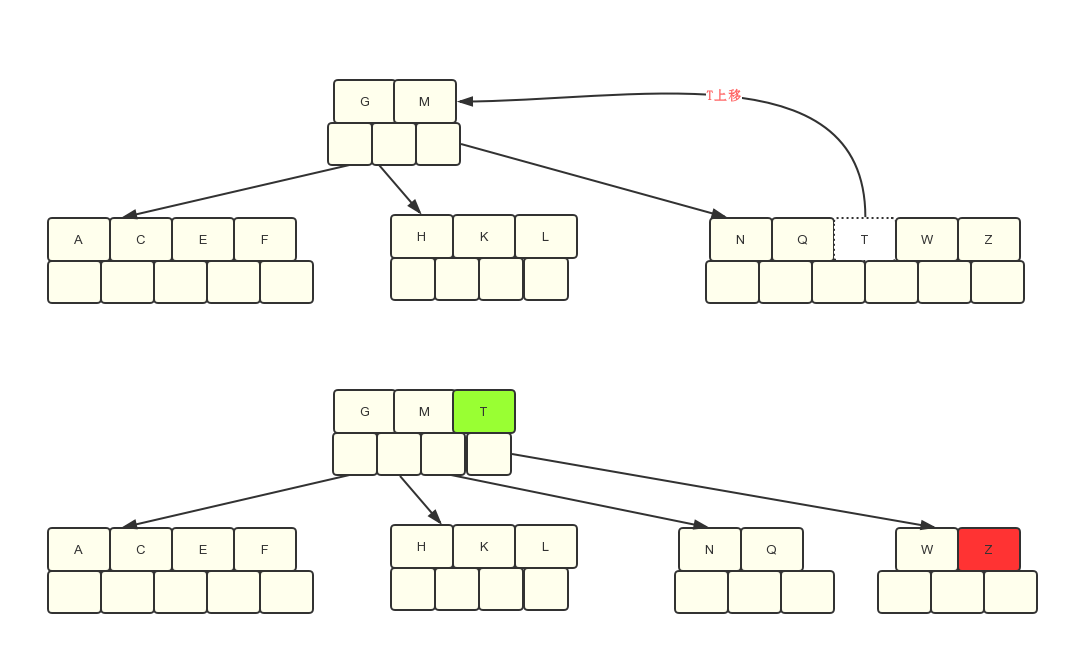
第7步：插入D，导致最左边的需要分裂，插入P，R，X，Y插入不需要分裂

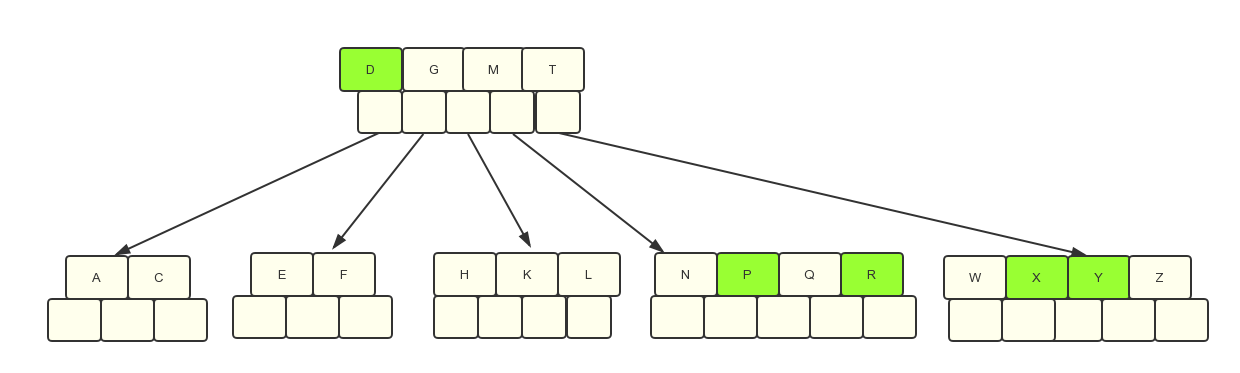
第8步：最后插入S时，我们来看下分裂过程：
根节点上M–>T指向的是第四个孩子节点，第五个孩子节点上都是大于T的字母，因此S应该是插入到第四个节点上去。
在分裂过程中上移Q节点的时候发现导致父亲结点的关键字个数也大于m-1了，需要继续向上分裂。
在分裂DGMTQ时需要先进行排序，最终结果是DGMQT，然后在将M节点分裂，向上操作。

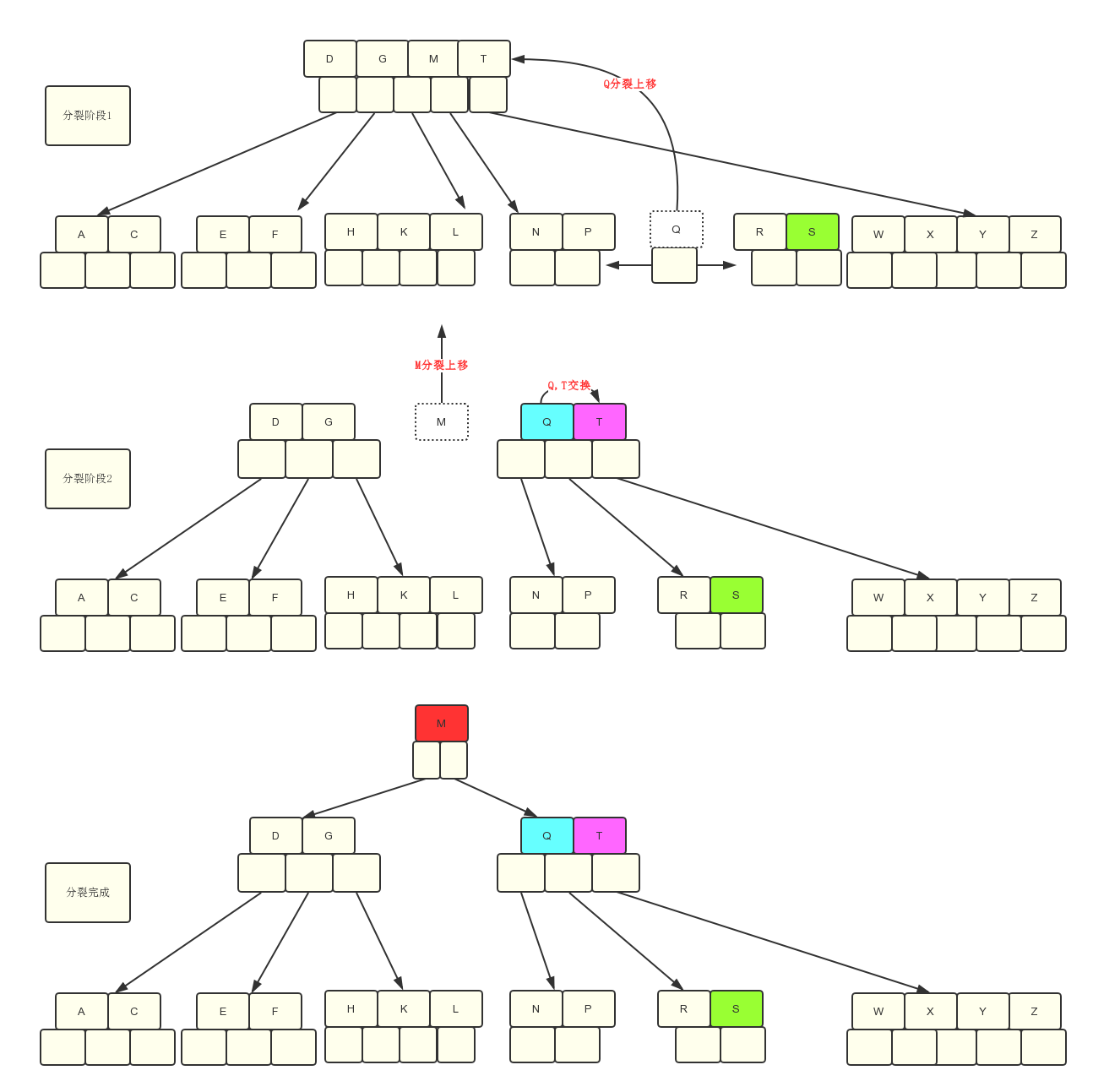
B树的插入总结

对于上面插入的过程，我们可以看见，有的是直接插入，有的需要进行“分裂”，但是我们注意到对于非叶子节点，我们没有直接插入数据，这些非叶子节点都是分裂出来的，根节点也同样，如果只有一个元素，那它就是根节点。

• 1.插入一个元素时，首先检查是否存在，如果不存在，则在叶子节点插入该数据（需要注意的是在插入过程中可能产生关键字的右移）。

• 2.如果叶子节点的空间满了，也就是关键字数目条件不满足时（Ceil[m/2]-1 <=n <= m-1），需要进行分裂操作，操作的原则是将此时的关键字分成两半，各形成两个新的节点，而中间节点则上升成为父节点（同样的，如果此时父节点也满了，也需要进行分裂）。

• 3.在分裂过程中伴随着还有对应指针的移动，通过关键字可以看出左指针指向的数据比右指针指向的数据小。

• 4.如果根节点满了的话，会造成根节点关键字的上移，树的高度增加一层。

B树的删除

删除的时候也需要关注的一个最重要的点就是关键字个数，需要保证n在[2,4]之间，也就是Ceil[5/2]-1 <= n <= m-1

上面插入之后的最终结果如图1，删除也是基于图1进行

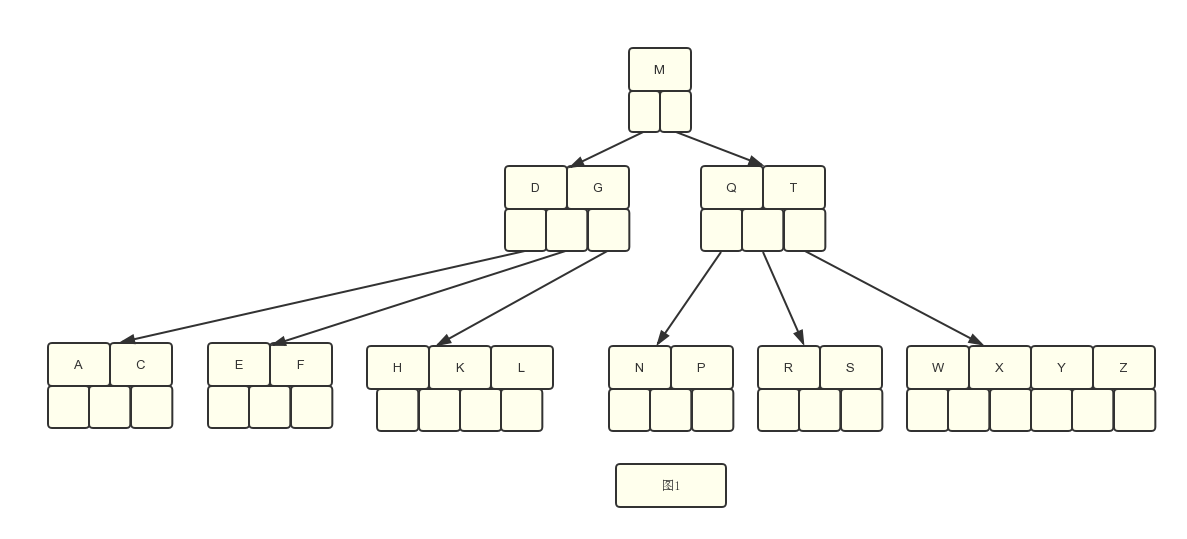
1. 基于图1，假设我们先删除H，可以看见H是在叶子节点中，并且叶子节点的关键字是3>2,所以它可以直接删除，然后K和L前移就ok了。见图2
   这是情况一：直接删掉
   
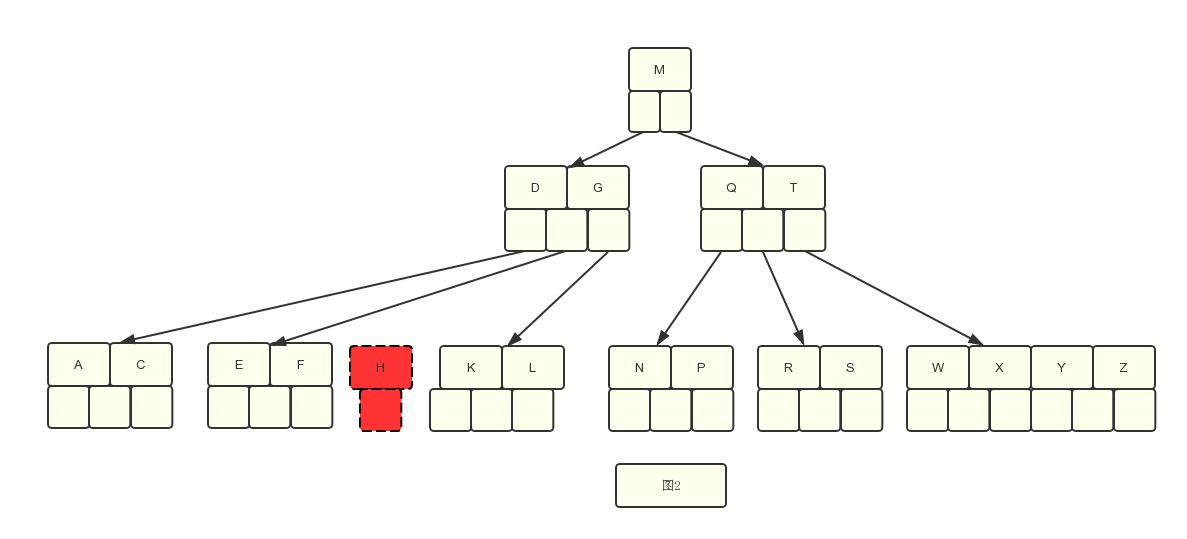
   2.基于图1 假设我们要删除T，T是在非叶子节点中，对于非叶子节点中的关键字K
   需要使用其中序前驱（这里是S）（或后继（这里是W））关键字K’代替K，然后从叶子节点中删除K’（如果删除k’不破坏规则直接删除即可，如果删除之后导致关键字个数少于Ceil[5/2]-1，则需要调整，下面会提到）。
   （注意此处可以直接删除叶子节点中的K’也就是W，是因为叶子节点的数目是4>2）见图3.
   这是情况二：借前驱或后继
   
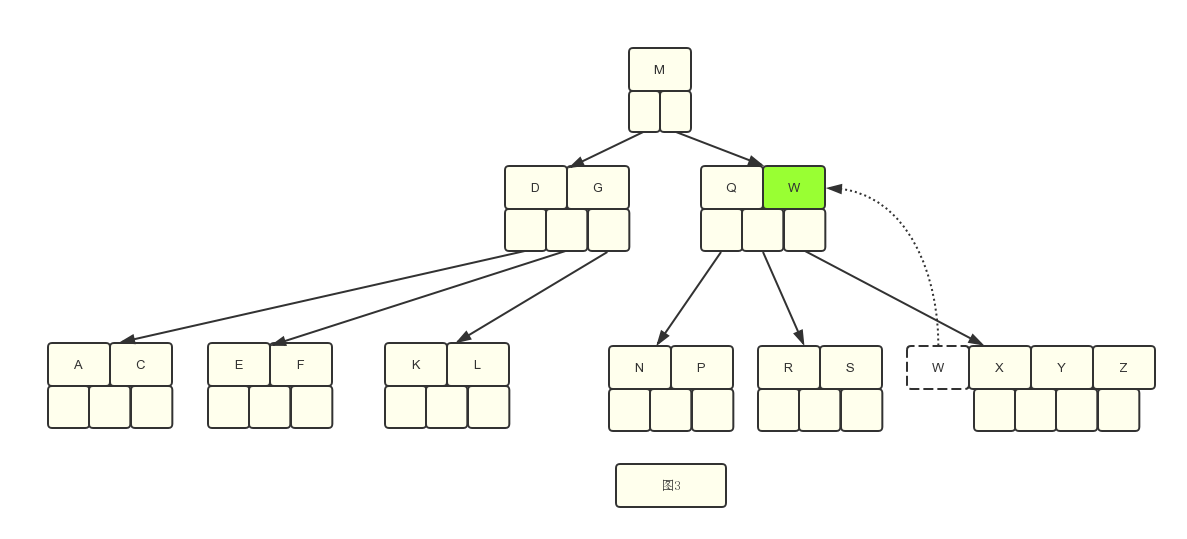
   3.基于图3，我们删除R关键字
   我们发现R在叶子节点中，并且此叶子节点的关键字数目是2 == 2，因此如果直接删除的话就会破坏掉B树的结构，所以需要“借”，怎么借是关键，“借”的方法很简单。
   情况三：从右边兄弟结点借
   看它兄弟姐妹有没有富余关键字，观察“NP”和“XYZ”两个兄弟节点，发现在其右边的兄弟XYZ”的关键字数目是3>2，因此它时有富余的，可以借一个过来。而且借的这一个在右边节点中，因此是借最左边一个（因为选择右边节点的话最小的关键字是在最左边，这样移动不会破坏B树的顺序），见图4–1和图4–2.
   
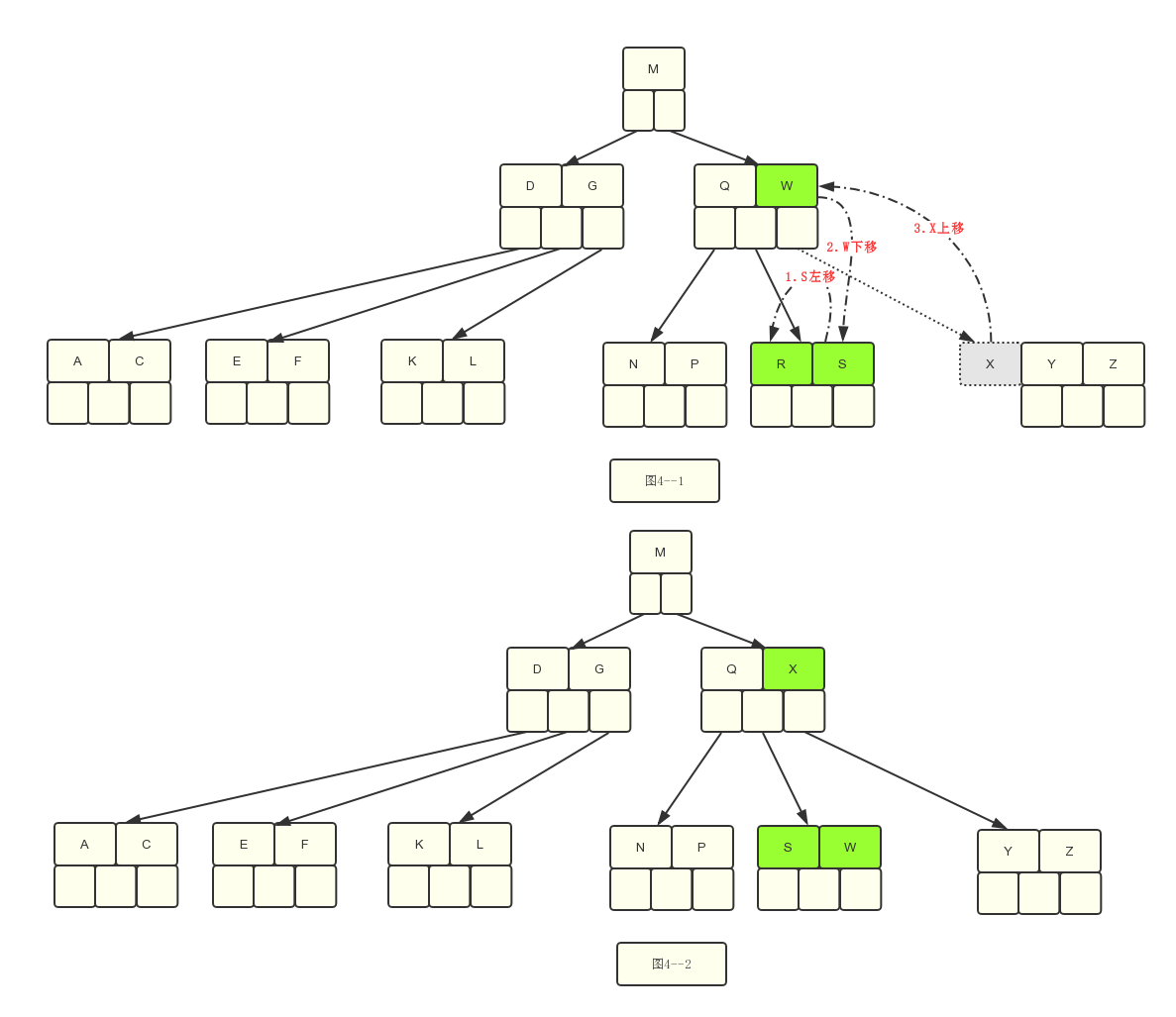
   4.还有一种情况是删除R时发现左边节点的数据满足要求。
   (所以在选择左边节点时需要移动最右边的关键字)进行移动。见图5–1和图5–2.
   需要注意的是R和S的关系，B树的特点就是左边永远小于右边，所以有点地方会存在左右移动的情况。
   这是情况4：从左边兄弟结点借
   

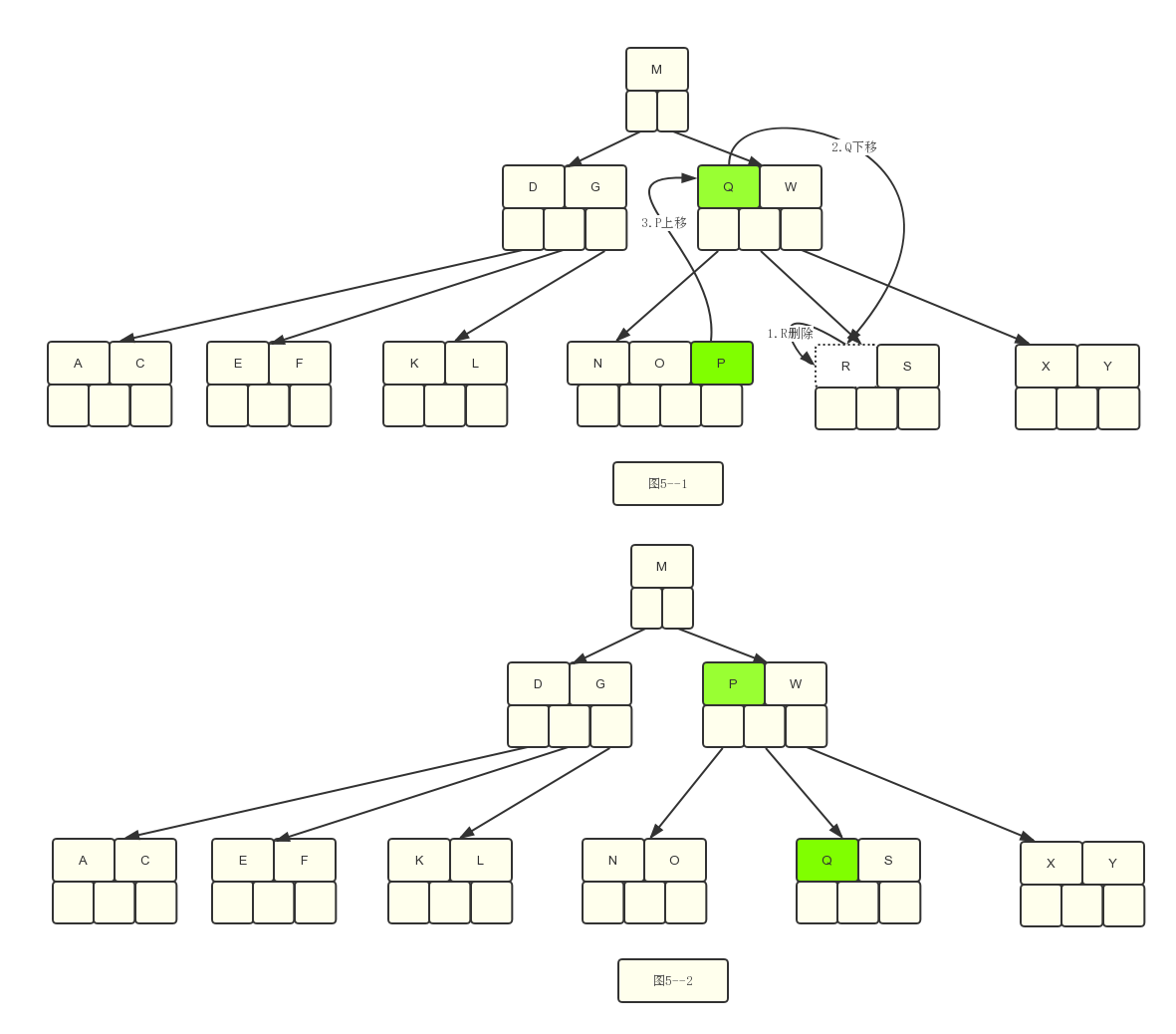
5.1 难点来了，假设现在基于图5–2我们删除关键字E
发现左右都不富余，我们先跟着例子走，下面说规则。
情况5：和兄弟结点合并

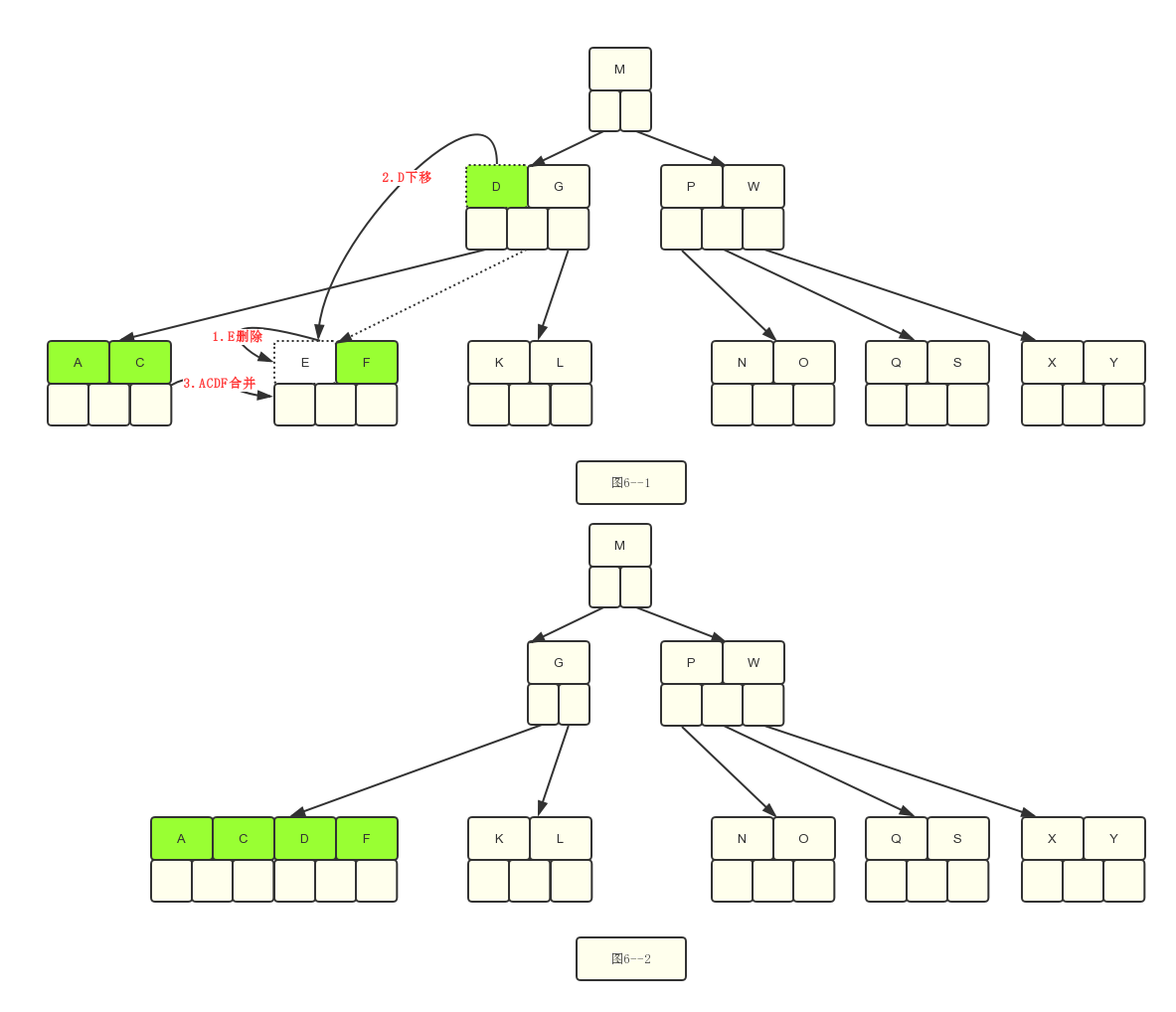
5.2 此时结果就是图6–2，但是呢，父节点只有一个关键字G，并不满足[2,4]的要求，所以这个时候还是需要继续移动，以满足B树的要求。我们来看怎么移动。
可以想借的办法，但是G的兄弟节点，“PW”刚好满足最小值2，所以它借不了，借不了，那只能是合并了，因此需要合并G和PW，合并的时候需要下移父亲节点M。

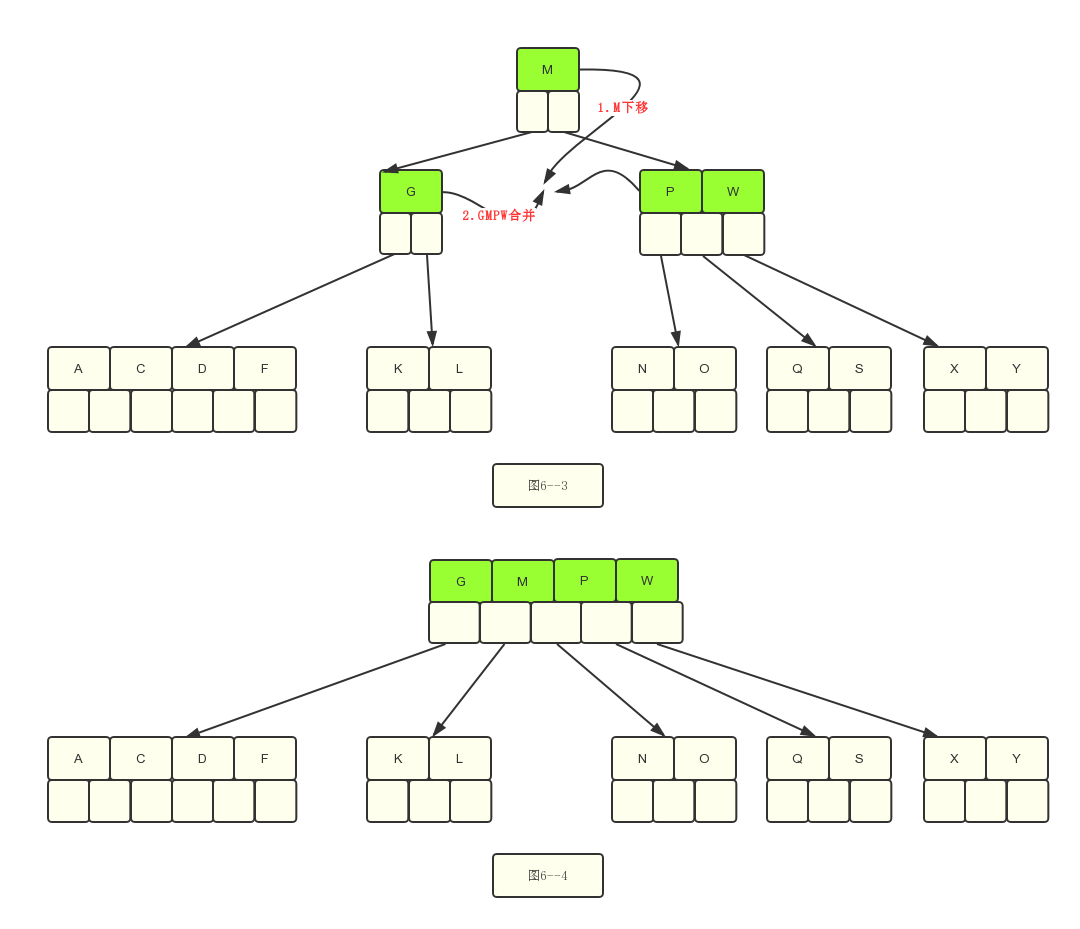
5.3，步骤5.2里面需要合并的原因是兄弟节点不能借，我们来看看能借的情况下是怎么移动的？
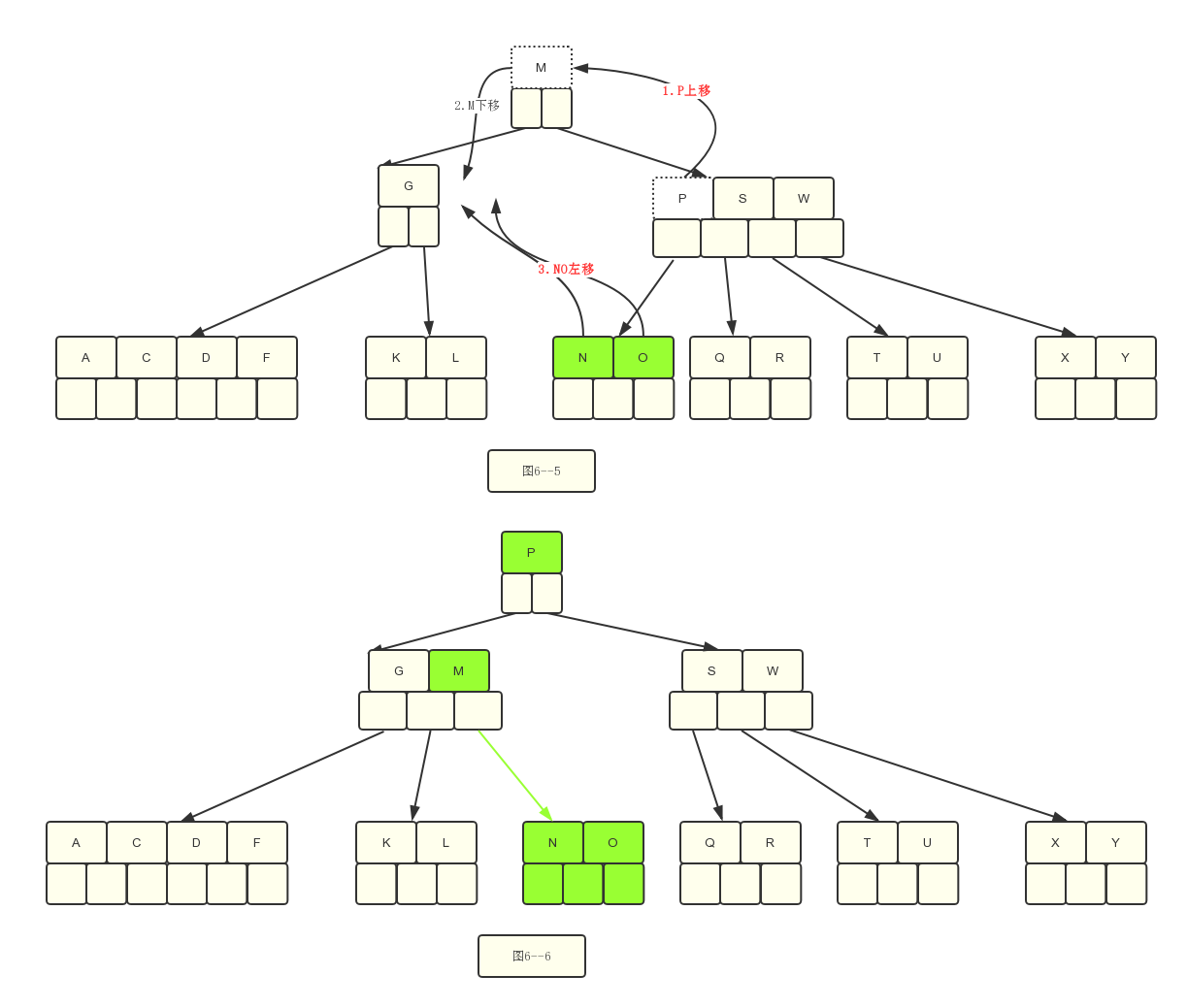
这个时候G节点的关键字只有1 个< 2，同时又发现兄弟节点“PSW”的关键字是3>2，可以借一个过来，借右边的关键字的话，要拿右边的最左边的关键字P。
所以P上移，M下移到G节点中，但是此时和步骤4的图5–1不同的是，M和P关键字之间是存在节点NO的，因此需要移动NO跟在M后面才行，详情见下图。这一例子是借右边节点，同理可以模拟借左边节点，一样的道理。
这是情况6：合并的的时候要移到孩子结点，以保持左边小于右边

B树的删除总结

删除操作总的来说比较繁琐，繁琐的地方在于要维护B树的特性。怎么维护B树特性，两个重要的方法是“合并”节点和“借”关键字。依据的原则依然是关键字数目（Ceil[m/2]-1 <=n <= m-1）。

• 1.如果删除的是叶子节点上的数据，删除之后移动元素保证该叶子节点顺序不变。

  • 1.1 如果此时关键字个数依然满足条件，则删除结束。

  • 1.2 如果此时关键字个数小于条件个数，则需要进行移动。

    • 1.2.1首先看其相邻兄弟节点是否有富余关键字，如果有，则将两个节点中间的父节点的关键字下移到当前要删除节点内，注意此处放入的时候需要保持顺序，然后将富余节点的最左（最右）关键字上移到父节点中，然后删除该关键字。（此处需要注意图6–5的情况）

    • 1.2.2如果其相邻兄弟节点没有富余关键字了，则需要将该节点和相邻节点进行合并（选择左右没关系，但是要保证顺序的一致就行），移动的规则是将父节点（父节点必须在两个需要合并的节点之间）下移到改节点中被删除的关键字处，然后记性合并操作，操作之后可能父节点能满足数目条件，如果不满足的话，仍然再次执行1.2.1 --> 1.2.2的步骤，简要的说就是先看相邻兄弟节点是否富余，富余的话借父节点，不富余的话就合并。

• 2.如果删除的是非叶子节点上的数据，非叶子节点特殊性在于它存在孩子节点。

  • 2.1 首先将该关键字的后继节点中的最左边上移到该位置（这个最左边是指中序遍历后继节点中最左边的节点），如果后继节点上移一个关键字之后满足数目条件，则结束。

  • 2.2 后继节点数目不满足条件数目了，则需要观察能否进行借的操作，如果不能借，则需要合并，和叶子节点操作类似。

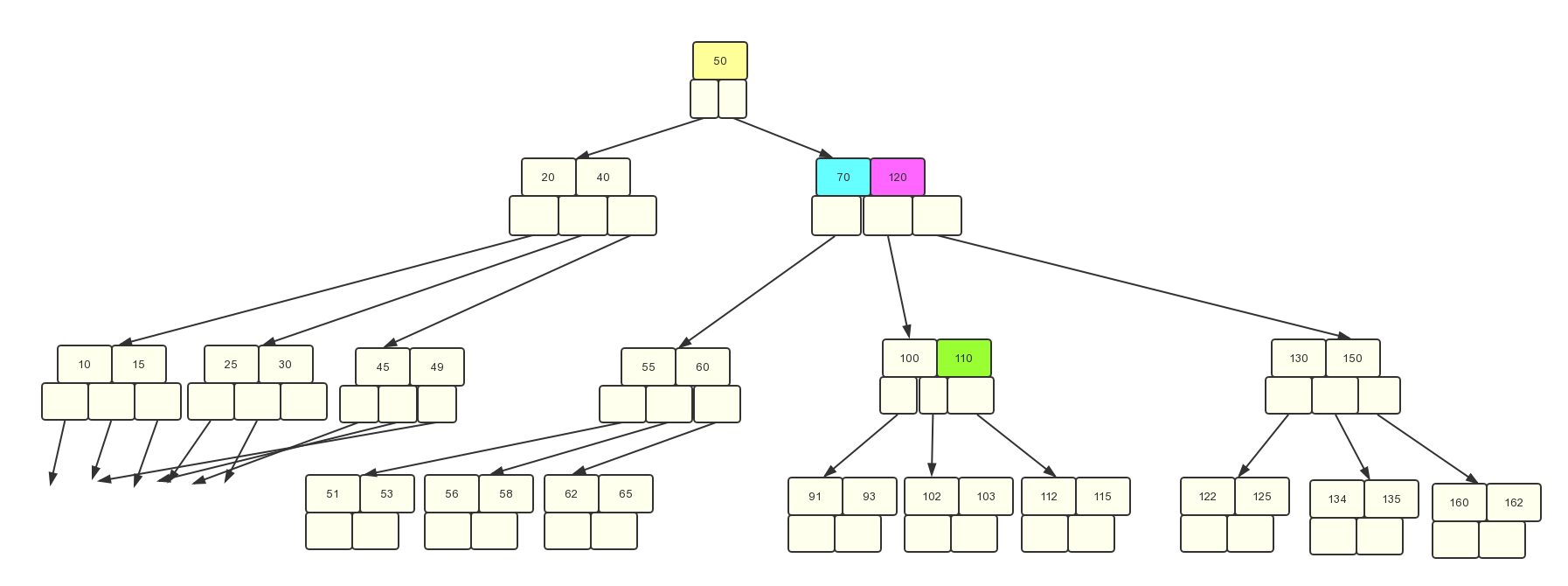
最后再贴一个删除例
删除120

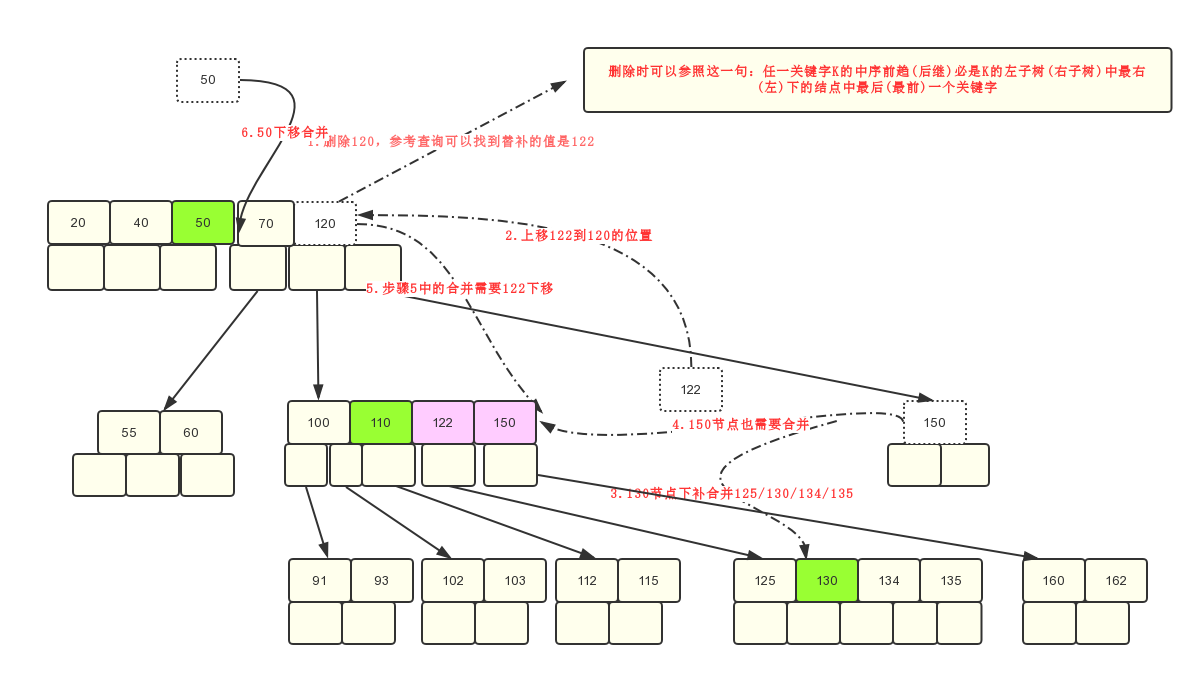
参考博客：https://blog.youkuaiyun.com/qq_32924343/article/details/80167184