神经网络继续学习

感知机模型解决逻辑运算问题

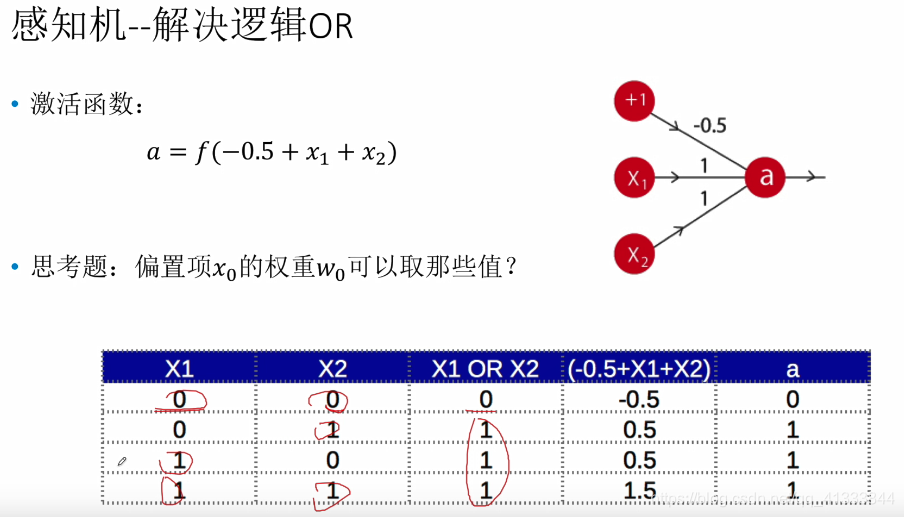
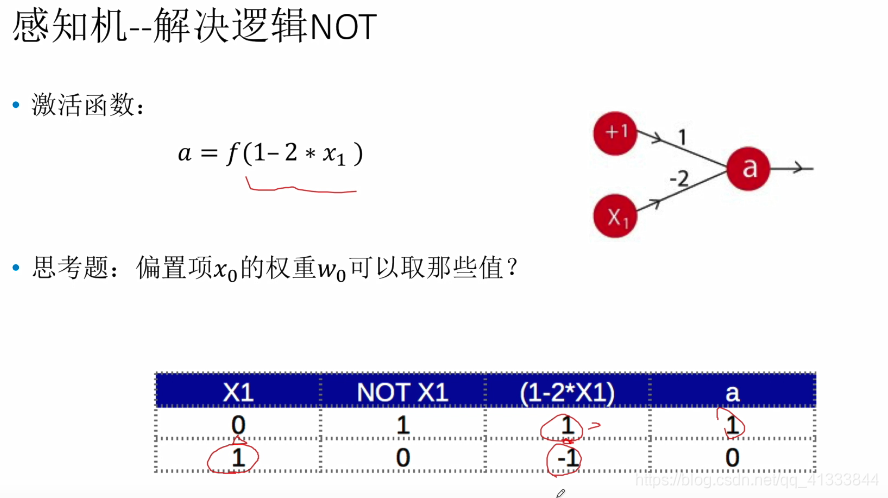
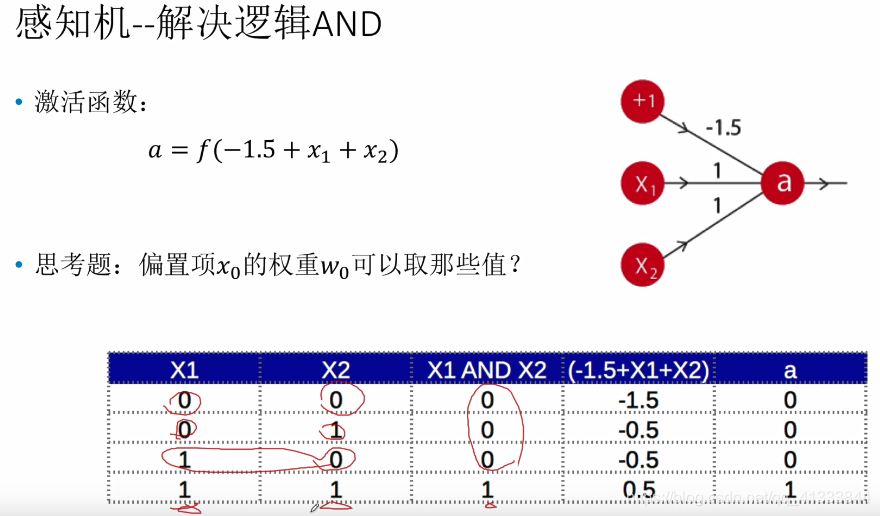
神经网络雏形，明白一些怎么进行分类的了，这里的参数都是人工尝试的。

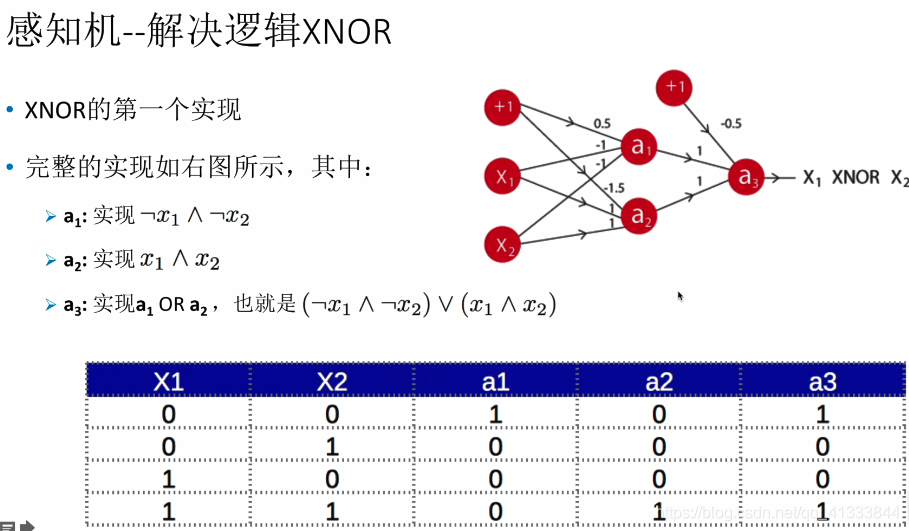
训练感知机模型时，数据一定要是线性可分的，否则使用梯度下降算法将无法收敛。

 

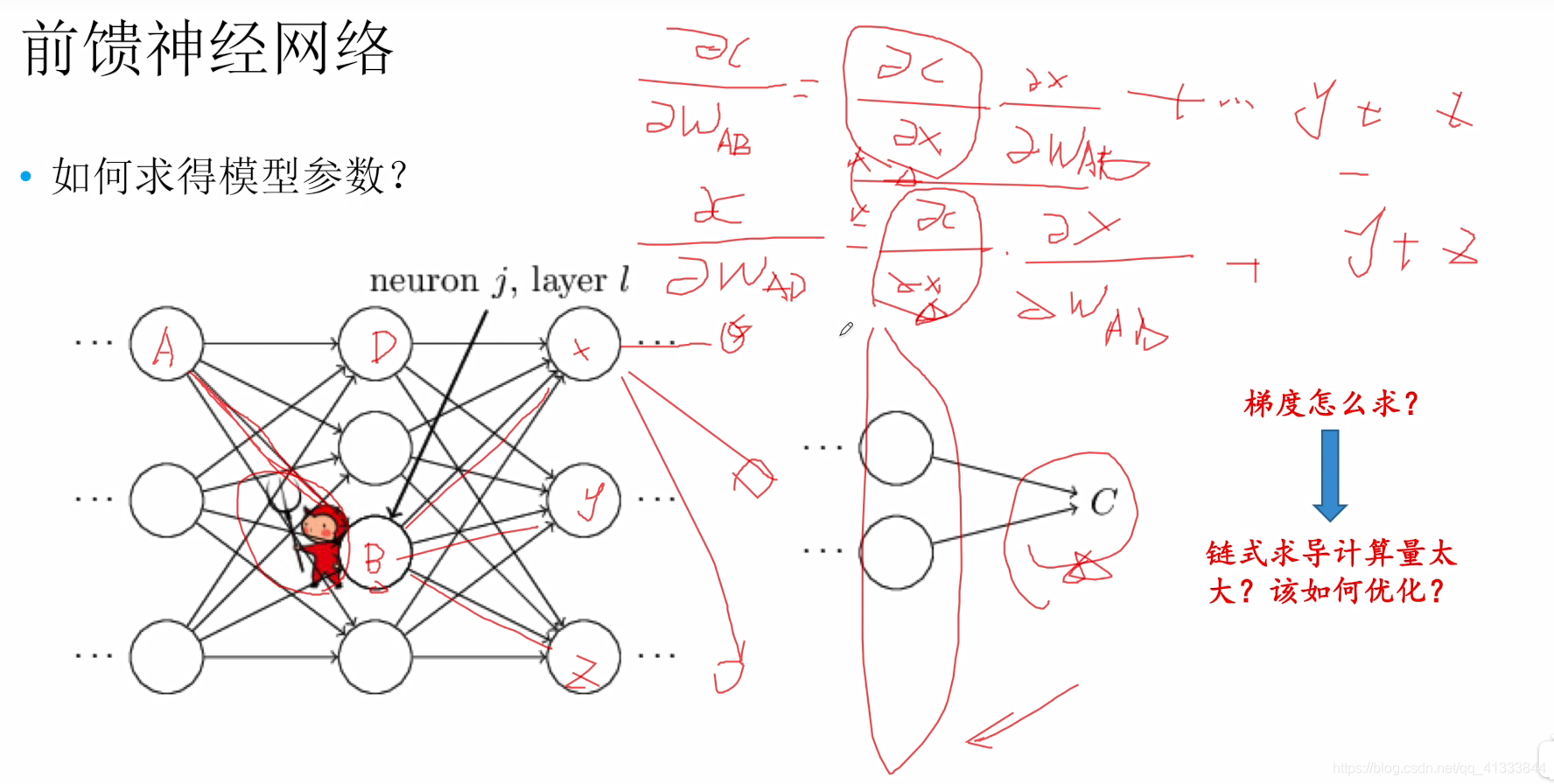
前馈神经网络（整个网络无反馈，可以使用有向无环图表示）

【个人想法】为什么选择sigmoid函数，而不继续使用sign函数1、选择连续函数可以进行求导

2、被选择的这些函数方便进行求导，比如1/（1+exp(-x)）

3、能更加准确的表示输入与输出的关系，输入小的变化不至于输出发生巨大的变化

详细介绍常用的激活函数

https://blog.youkuaiyun.com/tyhj_sf/article/details/79932893

https://mp.weixin.qq.com/s?src=11&timestamp=1563888003&ver=1746&signature=mNTCYeTvn-UuTRdJ6a08C6f0xH-mC8qmT7l4ggFJeU6bwBKoGbXS1Y1lDsb8WelPPlkT5DZM*RaxaoJ6iK9vi32r3qsS7OHggaM*JtZ8YYFnvUQDGkAxpsG1JYJGAvqs&new=1

 

对损失函数求梯度存在的问题：【计算量大】

1、对单个权值求偏导计算量大（当神经网络层数增加时计算量将会按照指数级别上升）

2、并且对不同的权值进行偏导计算时存在冗余计算。比如Wba、Wda的计算都依赖下一层的梯度，在计算 Wba时有些已经计算过了，但是在计算Wda时又会再一次进行计算

 

优化途径：【记忆化进行记录查询】

1、从输入层开始计算，计算过的（已经被记录了）偏导数直接查表使用，对新计算的偏导数进行记录（记忆化的表、记忆化搜索）递归（伪递归）可以使用while或者for循环代替【其实与bp等效】

2、因为本层的梯度计算要用到下层的梯度、下下层的梯度、下下下层的梯度……存在大量冗余计算。所以可以选择直接从最后一层进行计算，倒着进行，也是记录查询。【bp算法】

 

参考视频解惑者https://www.bilibili.com/video/av43414082?t=227

【链式法则】即是数学上的复合函数求偏导数

BP算法【误差反向传播算法】

公式推导https://space.bilibili.com/397540782/channel/detail?cid=65054

高效的求解神经网络的权重系数的算法，本质还是梯度下降算法，只不过是在求梯度的过程中进行了优化   

链式法则还是bp算法

收敛与局部极值