PAT-BASIC1070——结绳/PAT-ADVANCED1125——Chain the Ropes

最新推荐文章于 2024-09-29 22:31:08 发布

原创最新推荐文章于 2024-09-29 22:31:08 发布 · 340 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#PAT甲级乙级 #贪心算法 #结绳

PAT甲级真题题解同时被 2 个专栏收录

155 篇文章

订阅专栏

PAT乙级真题题解

94 篇文章

订阅专栏

本文深入解析PAT竞赛中BASIC1070与ADVANCED1125两道题目的解题思路，通过贪心算法实现绳子的最大长度计算，提供C++代码实现，并附有详细解释。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

我的PAT-BASIC代码仓：https://github.com/617076674/PAT-BASIC

我的PAT-ADVANCED代码仓：https://github.com/617076674/PAT-ADVANCED

原题链接：

PAT-BASIC1070：https://pintia.cn/problem-sets/994805260223102976/problems/994805264706813952

PAT-ADVANCED1125：https://pintia.cn/problem-sets/994805342720868352/problems/994805350316752896

题目描述：

PAT-BASIC1070：

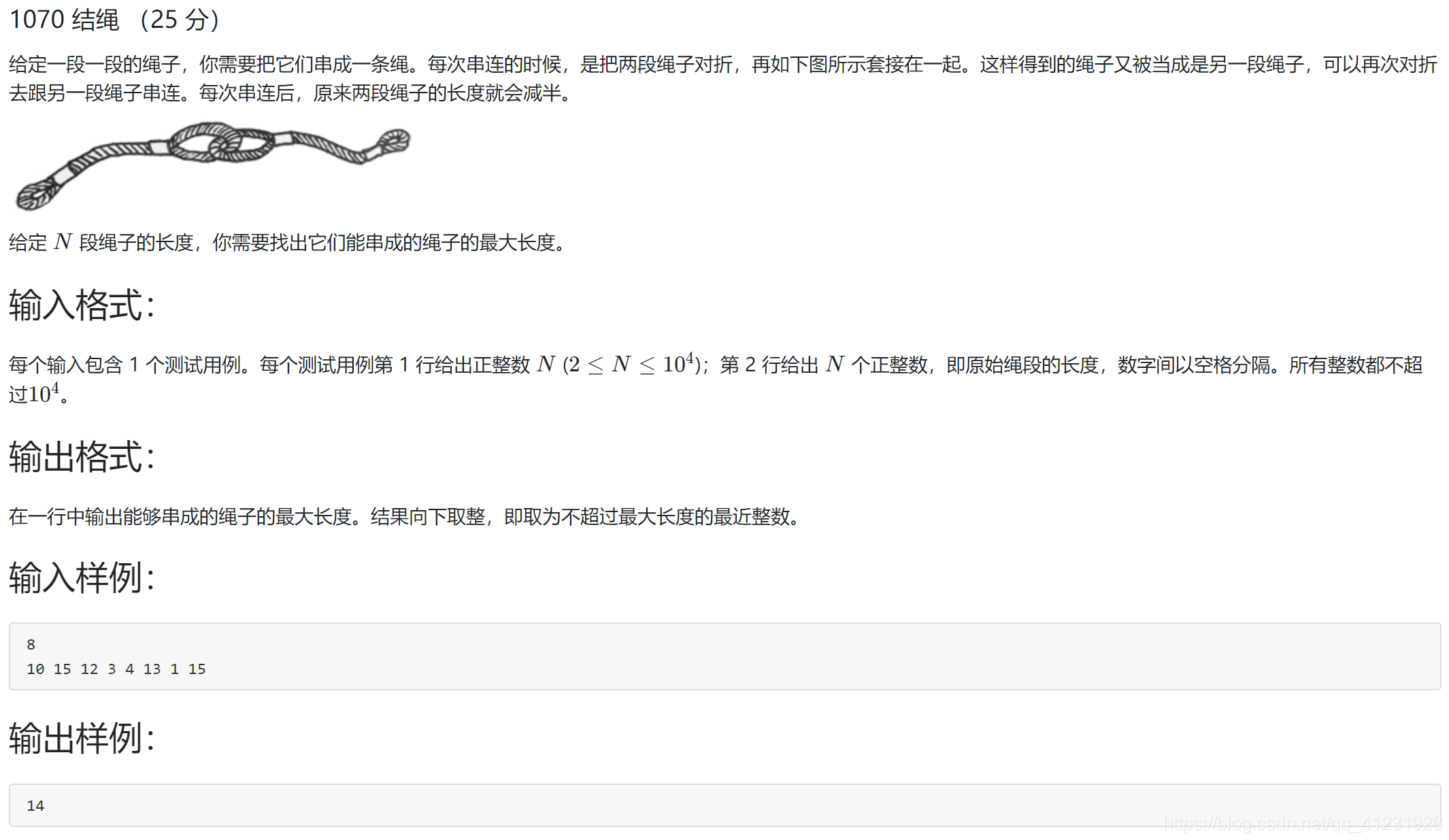
PAT-ADVANCED1125：

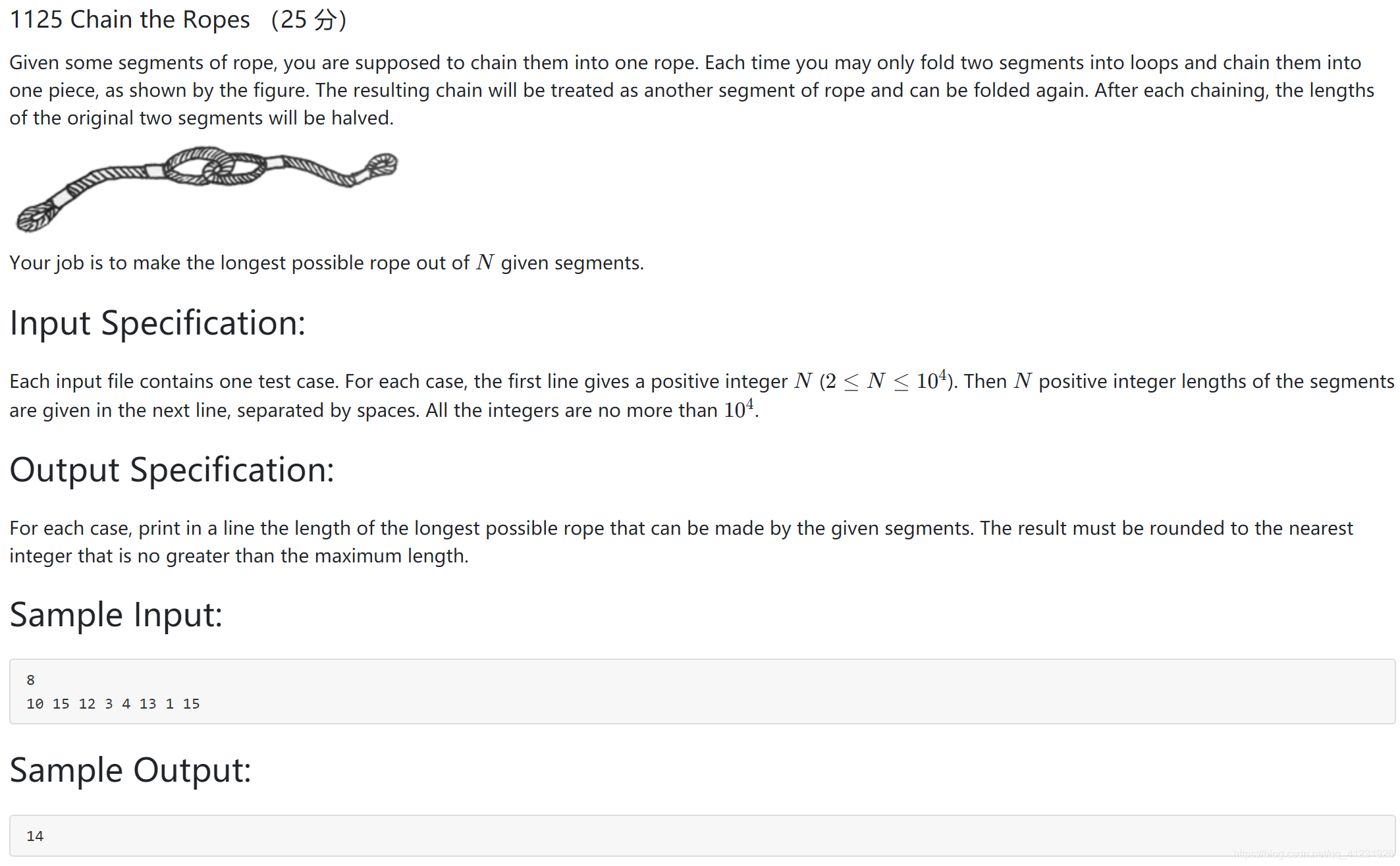
知识点：贪心算法

思路：先从小到大排序，再依次结绳

为什么从小到大排序后，再依次结绳所得到的绳子的长度最大呢？

假设一个序列[a1, a2, a3, a4, ..., a(n - 1), an]，其中a1 <= a2 <= a3 <= ... <= a(n - 1) <= an。交换其中任意两者的位置，为便于分析，我们假设交换[a(n - 1), an]的位置，则序列变成了[a1, a2, a3, a4, ..., an, a(n - 1)]。

假设[a1, a2, ..., a(n - 2)]的结绳后的长度为k。对于序列[a1, a2, a3, a4, ..., a(n - 1), an]，其结绳后的长度为(k / 4 + a(n - 1) / 4 + an / 2)，而对于序列[a1, a2, a3, a4, ..., an, a(n - 1)]，其结绳后的长度为(k / 4 + a(n) / 4 + a(n - 1) / 2)，由于我们前面假设了a(n - 1) <= an，因此(k / 4 + a(n - 1) / 4 + an / 2) >= (k / 4 + a(n) / 4 + a(n - 1) / 2)，即序列[a1, a2, a3, a4, ..., a(n - 1), an]的结绳长度大于等于序列[a1, a2, a3, a4, ..., an, a(n - 1)]的结绳长度。

这就证明了从小到大排序后的序列[a1, a2, a3, a4, ..., a(n - 1), an]的结绳长度是最大的。

结绳过程中用浮点数类型进行计算，最后输出结果时转换为int类型。

时间复杂度是O(NlogN)。空间复杂度是O(1)。

C++代码：

#include<iostream>
#include<algorithm>

using namespace std;

int main(){
	int N;
	scanf("%d", &N);
	double nums[N];
	for(int i = 0; i < N; i++){
		scanf("%lf", &nums[i]);
	}
	sort(nums, nums + N);
	double result = nums[0];
	for(int i = 1; i < N; i++){
		result = (result + nums[i]) / 2;
	}
	printf("%d\n", (int)result);
	return 0; 
}

C++解题报告：