2019牛客网多校第八场J：Just Jump题解

原创于 2019-08-15 02:20:34 发布 · 192 阅读

1 ·

CC 4.0 BY-SA版权

训练题解专栏收录该内容

4 篇文章

订阅专栏

本文深入探讨了Lucas定理在解决大规模数据范围组合数计算问题的应用，尤其是在1e7级别的数据处理中。通过实例解析，详细阐述了如何利用Lucas定理优化组合数的计算，同时介绍了将问题转化为从特定点中选取点的方案数的技巧，以及使用容斥原理处理复杂情况的方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目链接
思路：

补充：
1.由于数据范围达到1e7，只能通过lucas定理计算组合数。
2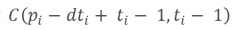 这个公式是怎么这个公式的推导过程：需要刚好花时间ti到达距离pi，每次移动至少d的方案数，等价于花时间ti到达距离pi-dti，每次不一定要移动的方案数。这个问题又可以转化成从pi-dti+ti-1 个点中选取ti-1个点的方案数。
3.gu[u][i] :受到含第i次攻击在内，一共收到奇/偶次攻击的情况数，再根据容斥原理，奇加偶减。

（这种题真是太难debug了，基本上就是照着ac代码一步一步调）

#include<bits/stdc++.h>
using namespace std;
typedef long long ll ;
const int MOD=998244353;
const int MAXN=1e7+5;

ll INV[MAXN],fac[MAXN],fac_p[MAXN];
ll num[2][MAXN],sum[MAXN],f[MAXN];
int L,d,m;
struct node {
    ll p,t;
    bool operator<(node y){
        return t<y.t;
    }
}nodes[3005];

ll powa(ll a, ll b){
    ll ans = 1;
    a %= MOD;
    while(b){
        if(b & 1)ans = (ans % MOD) * (a % MOD) % MOD;
        b /= 2;
        a = (a % MOD) * (a % MOD) % MOD;
    }
    ans %= MOD;
    return ans;
}


ll C(ll n, ll m){
    if(n<0||m<0)return 0;
    if(n<m) return 0;
    return fac[n]*fac_p[n-m]%MOD*fac_p[m]%MOD;
}
ll Lucas(ll n, ll m){
    if(n<0||m<0) return 0;//一定要提前判断n,m的正负，否则算出来的结果会相差很大。
	if(m==0) return 1;
    return C(n %MOD, m % MOD) * Lucas(n / MOD, m / MOD) % MOD;
}

void init(){
    fac[0]=1;
    for(int i=1;i<MAXN;i++) fac[i]=fac[i-1]*i%MOD;
    fac_p[MAXN-1]=powa(fac[MAXN-1],MOD-2);
    for(int i=MAXN-2;i>=1;i--) fac_p[i]=fac_p[i+1]*(i+1)%MOD;
}

int main()
{
	scanf("%d%d%d",&L,&d,&m);
	f[0]=sum[0]=1;
    init();
    for(int i=1;i<=L;i++)
	{
		if(i<d) f[i]=0;
		else f[i]=sum[i-d];
		sum[i]=(sum[i-1]+f[i])%MOD;
	}
    nodes[0].p=nodes[0].t=0;
    for(int i =1;i<=m;i++) {
        scanf("%lld %lld",&nodes[i].t,&nodes[i].p);
    }
    sort(nodes+1,nodes+m+1);
    ll ans=f[L];
    num[0][0]=1;
    for(int i=1;i<=m;i++){
        for(int k=0;k<2;k++){
            for(int j=0;j<i;j++){
                ll dp=nodes[i].p-nodes[j].p,dt=nodes[i].t-nodes[j].t;
                //printf("%lld %lld:%lld\n",dp-d*dt+dt-1,dt-1,Lucas(dp-d*dt+dt-1,dt-1));
                num[k][i]=(num[k][i]+num[1-k][j]*Lucas(dp-d*dt+dt-1,dt-1)%MOD)%MOD;
            }
        }
        ans=(ans+(num[0][i]-num[1][i]+MOD)%MOD*f[L-nodes[i].p]%MOD)%MOD;
        
    }
    printf("%lld\n",ans);
}