前情提要:SLAM问题用两个方程描述
运动方程:
x
k
+
1
=
f
(
x
k
,
u
k
)
+
w
k
观测方程:
z
k
,
j
=
g
(
x
k
,
y
j
)
+
v
k
,
j
运动方程:x_{k+1}=f(x_k,u_k)+w_k \\ 观测方程:z_{k,j}=g(x_k,y_j)+v_{k,j}
运动方程:xk+1=f(xk,uk)+wk观测方程:zk,j=g(xk,yj)+vk,j
其中,
k
k
k为离散时刻
x
x
x—位置
u
u
u—输入
w
w
w—该过程加入的噪声
z
k
,
j
z_{k,j}
zk,j—
z
z
z时刻对第
j
j
j个路标点的观测数据
y
j
y_j
yj—第
j
j
j个路标点
v
k
,
j
v_{k,j}
vk,j—观测噪声
问题:
- x k x_k xk如何表达
- f , g f,g f,g如何表达
- u , z u,z u,z–> x , y x,y x,y
1 点与坐标系
-
坐标系(参考系)
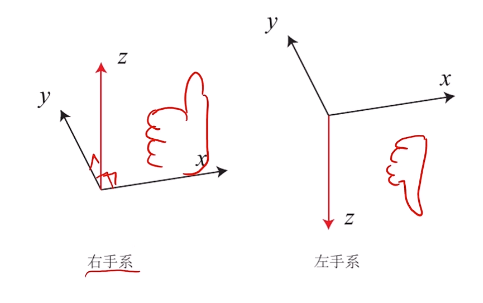
-
点
-
向量
内积(点乘)
外积(叉乘)
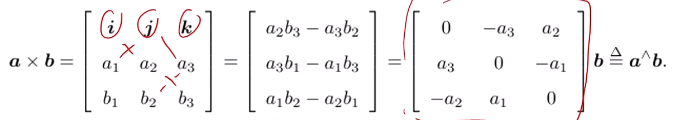
叉积计算可以转换为矩阵与向量相乘

-
向量的坐标
https://zhuanlan.zhihu.com/p/622668371
2 旋转矩阵

R
R
R称为旋转矩阵
-
R
R
R是一个正交矩阵
R − 1 = R T R^{-1}=R^{T} R−1=RT
R T R = I R^{T}R=I RTR=I - R R R的行列式为+1
n维旋转矩阵的集合定义如下:
SO
(
n
)
=
{
R
∈
R
n
×
n
∣
R
R
T
=
I
,
det
(
R
)
=
1
}
\operatorname{SO}(n)=\left\{\boldsymbol{R} \in \mathbb{R}^{n \times n} \mid \boldsymbol{R} \boldsymbol{R}^{\mathrm{T}}=\boldsymbol{I}, \operatorname{det}(\boldsymbol{R})=1\right\}
SO(n)={R∈Rn×n∣RRT=I,det(R)=1}
S
O
(
n
)
SO(n)
SO(n)是特殊正交群

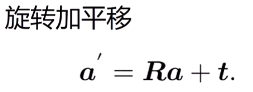
欧拉定理 (Euler’s rotation theorem):刚体在三维空间里的一般运动,可分解为刚体上方某一点的平移,以及绕经过此点的旋转轴的转动。
当表达复合情况时,增广方式构成齐次形式(homogeneous)
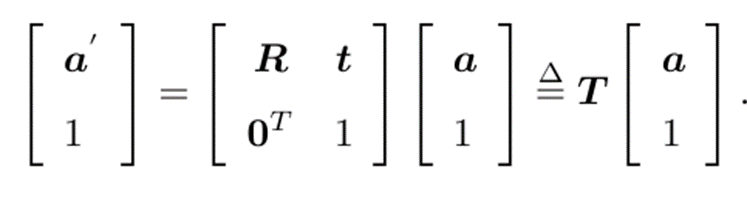
T
T
T为变换矩阵
齐次坐标
a
~
=
[
a
1
]
\tilde{a}=\begin{bmatrix} a \\ 1 \end{bmatrix}
a~=[a1]乘任意非零常数时仍表达同一坐标
a
~
=
[
a
1
]
=
k
[
a
1
]
\tilde{a}=\begin{bmatrix} a \\ 1 \end{bmatrix}=k\begin{bmatrix} a \\ 1 \end{bmatrix}
a~=[a1]=k[a1]
变换矩阵的集合称为特殊欧氏群
S
E
(
3
)
SE(3)
SE(3)(Special Euclidean Group)
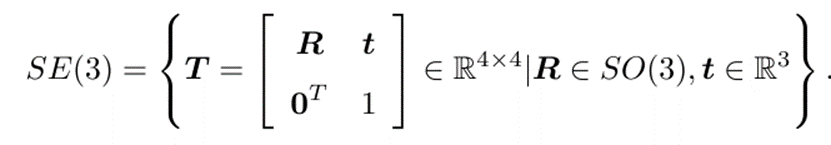
逆形式:
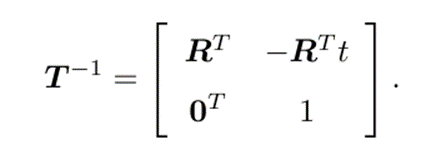
3 旋转向量和欧拉角
旋转矩阵具有冗余性,三个自由度用九个量表示
旋转向量
-
方向为旋转轴,长度为转过的角度
-
称为角轴/轴角 (Angle Axis) 或旋转向量(Rotation Vector)
已知旋转向量,求旋转矩阵

已知旋转矩阵,求旋转向量
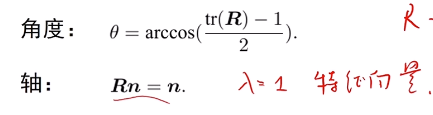
欧拉角
常见的有:yaw-pitch-roll,东北天
按Z-Y-X
绕定轴转或绕动轴转,顺序亦可不同(转前的轴还是转后的轴)存在万向锁问题
4 四元数
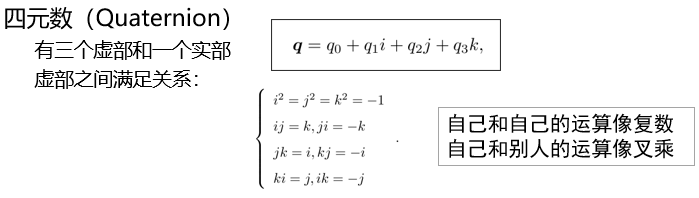
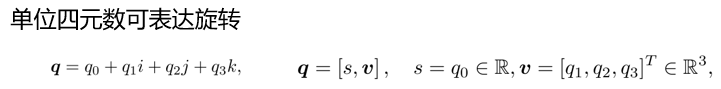
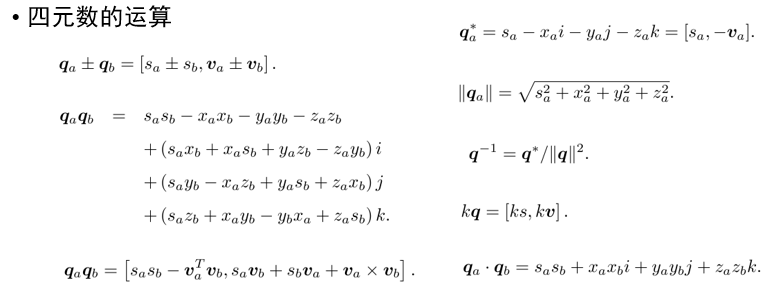
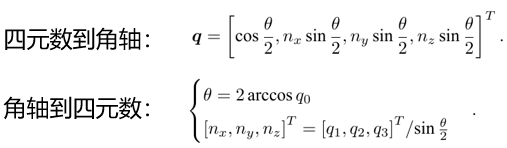





 本文探讨了SLAM问题中关键的数学概念,包括坐标系、旋转矩阵、旋转向量和欧拉角的表示与计算,以及四元数的应用,以解决定位与地图构建中的问题,最后提及了Eigen库在实践中的应用。
本文探讨了SLAM问题中关键的数学概念,包括坐标系、旋转矩阵、旋转向量和欧拉角的表示与计算,以及四元数的应用,以解决定位与地图构建中的问题,最后提及了Eigen库在实践中的应用。
















 1314
1314

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








