求最短路径的四种方法（Dijkstra，Floyd，Bellman-Ford，SPFA算法）

【前言】

还不知道图是什么的可以看看这篇：图的基本概念。

最短路径，即在网络（带权的图）中，求两个不同顶点之间的所有路径中，边的权值之和最小的那一条路径。第一个顶点为源点，最后一个顶点为终点。

【问题分类】

单源最短路问题（特定点到所有点的最短路）和多源最短路问题（任意两点之间的最短路）。其中又分为有向图和无向图，有权图和无权图。根据边权的正负，又分为带负权边和不带负权边的最短路。

【最短路算法】

无权图的单源最短路算法类似bfs算法的实现过程，依次遍历结点并将遍历到的现结点的所有邻接点（相邻连接的点）压入队列，继续遍历直到访问到所有结点。也可以看做是权值为1的有权图的单源最短路。

有权图的单源最短路算法：Dijkstra算法，运用了贪心的思想（类似Prim算法）。

【Dijkstra算法】 

• 令S={源点s + 已经确定了最短路径的顶点vi}
• 对任一未收录的顶点v，定义dist[v]为s到v的最短路径长度，但该路径仅经过S中的顶点，即路径{s->(vi∈S)->v}的最小长度。
• dist[w] = min{dist[w], dist[v] +<v,w>的权重}
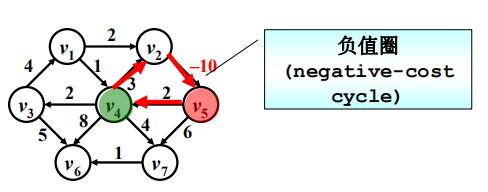
• 不适用于边权为负的情况,会出现负值圈。