【论文阅读】运动去模糊之BANet模型

【论文阅读】运动去模糊之BANet模型

BANet: A Blur-aware Attention Network for Dynamic Scene Deblurring（2022）

摘要：

图像运动模糊是物体运动和相机抖动共同作用的结果，这种模糊效果通常是方向性的且不均匀的。先前的研究尝试使用具有自注意力的自循环多尺度、多补丁或多时态架构来解决非均匀模糊，以获得不错的结果。然而，使用自循环框架通常会导致更长的推理时间，而像素间或通道间自注意力可能会导致内存使用过多。本文提出了一种模糊感知注意力网络（BANet），它通过单次前向传递实现准确高效的去模糊。我们的 BANet 利用基于区域的自注意力和多内核条带池来解开不同幅度和方向的模糊模式，并使用级联并行扩张卷积来聚合多尺度内容特征。 GoPro 和 RealBlur 基准测试的大量实验结果表明，所提出的 BANet 在模糊图像恢复方面的性能优于最先进的技术，并且可以实时提供去模糊结果。

‍

模型结构：

​​

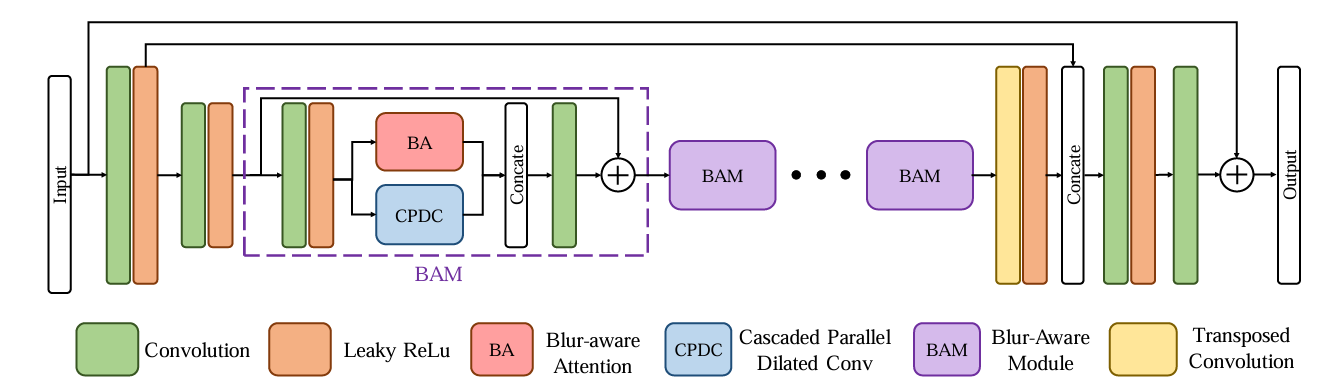
    BANet 从两个卷积层开始，其中步幅为 2，用于将输入图像下采样到一半分辨率。 末尾使用一个转置卷积层将特征上采样到原始大小。

    在这之间，堆叠一组 BAM 来关联具有相似模糊的区域并提取多尺度内容特征。 BAM 由两个组件组成：BA 和 CPDC，其中 BA 提取全局和局部模糊方向和幅度，CPDC 捕获多尺度模糊模式以自适应消除模糊。

模糊感知注意力（BA , Blur-awareAttention）的架构。它级联两部分，包括多内核剥离池（MKSP, Multi-Kernel StripPooling）和注意力细化（AR，Attention Refinement）。MKSP捕获不同幅度和方向的多尺度模糊模式，然后由AR在本地对其进行细化。

​​

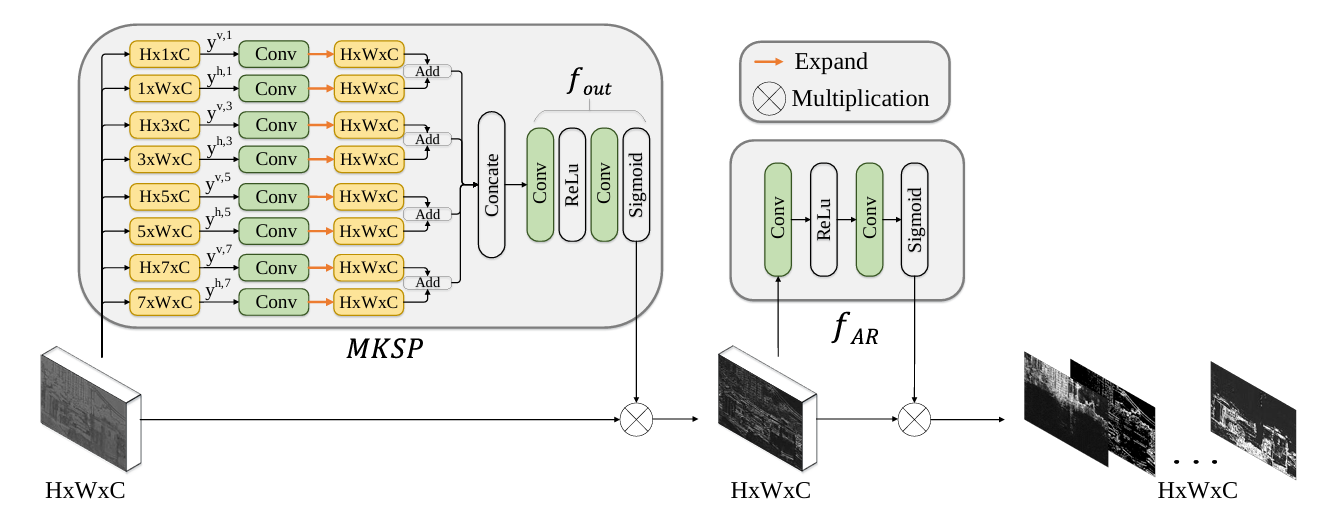
MKSP中，$y^{v,n}=[y_{i,j,c}^{v,n}],y^{h,n}=[y_{i,j,c}^{v,n}]$，n为不同尺度；

​ ​

$y_{i,j,c}^{v,n}=\frac{1}{K_h}{\sum }_{k=0}^{K_h-1}{x}_{i,(j\ast S_h+k),c}$ ；

$S_h=\lfloor \frac{W}{n}\rfloor ;K_h=W-(n-1)S_h；$

$y_{i,j,c}^{h,n}=\frac{1}{K_v}{\sum }_{k=0}^{K_v-1}{x}_{(i\ast S_v+k),j,c}$ ；

$S_v=\lfloor \frac{H}{n}\rfloor ；K_v=H-(n-1)S_v$ 。

即：将长度/宽度每隔n-1个像素取出，取平均，然后将平均后的列/行进行拼接。

卷积后再正交拼接：

$y_{i,j,c}^n=y_{i,\lfloor \frac{n\times j}{W}\rfloor ,c}^{v,n}+y_{\lfloor \frac{n\times i}{H}\rfloor ,j,c}^{h,n}$

即：把平均消掉的行/列通过复制恢复原来的大小，然后行生成的特征和列生成的特征对应元素相加。

四个尺度的在通道上拼接在经过$f_{out}(\ast )$输出注意力掩膜。

注意力掩码 $M_{mksp}$ 和输入张量的元素相乘获得全局关注特征后输入AR进行本地注意力细化。

‍

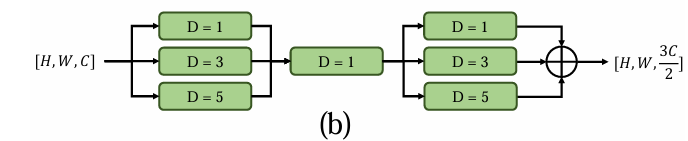
级联并行扩张卷积（CPDC，cascaded parallel dilated convolution ）（空洞卷积）

​​

‍

损失函数

$L_{char}=\sqrt{\Vert R-Y{\Vert }^2+{ϵ}^2}$，$ϵ=0.001$ ；

$L_{FFT}=\Vert F(R)-F(Y){\Vert }_1$；傅里叶变换

$L=L_{char}+\lambda L_{FFT},\lambda =0.01$；

‍

论文结果

​​

​​

​​

​​

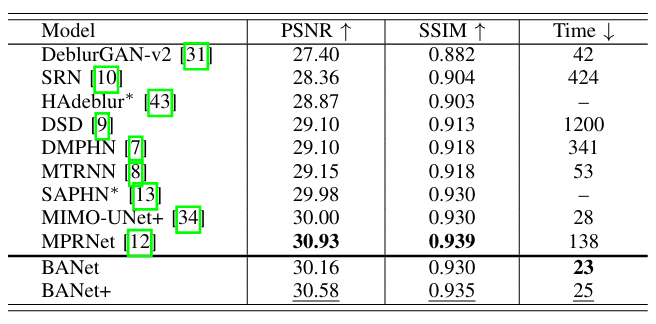
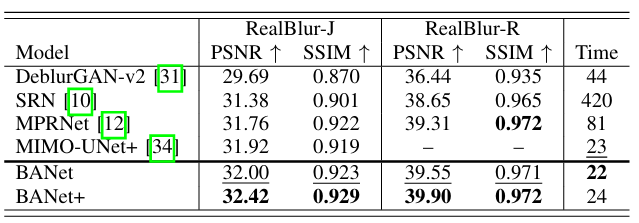
复现迁移：泛化能力较低，对真实数据集的效果不理想。

‍

论文：https://arxiv.org/pdf/2101.07518

Github：https://github.com/pp00704831/BANet-TIP-2022

‍

‍