VLSI数字信号处理系统——第十四章冗余运算

VLSI数字信号处理系统——第十四章冗余运算

作者：夏风喃喃
参考：
(1) VLSI数字信号处理系统:设计与实现 （美）Keshab K.Parhi／著
(2) socvista https://wenku.baidu.com/u/socvista?from=wenku

一. 引言

在普通的非冗余基r数字系统中，所有的数字都能够以唯一的方式表示。一个基r冗余有符号数位数字系统是允许任意数字可以有多种有符号格式表示，因此名为冗余。

冗余有符号数字系统的吸引人之处在于其“无进位”加法的性质。使得在除法和平方根操作的数位串行实现中非常有用，这些运算都是从最高数位(msd)开始计算的，最高数位优先冗余运算也被称为在线运算。

二. 冗余数表示

对称有符号数表示法：
使用数位集合 D < r , a > = { a ‾ , . . . , 1 ‾ , 0 , 1 , . . . , a } D_{<r,a>}=\{\overline{a},...,\overline{1},0,1,...,a\} D<r,a>​={a,...,1,0,1,...,a}，其中r为基，a为数位集合中最大数位。一个使用这种表示法的数字可以写为：

数字的符号由最高的非零数位的符号给定。

冗余度：
有符号数位表示法的冗余度用冗余因子ρ来度量，ρ定义为：
$$\rho =\frac{\alpha }{r-1}$$

可以用有符号表示法表示的数字范围是$[-\rho (r-r^{-W+1}),\rho (r-r^{-W+1})]$。该范围取决于字长W和冗余因子ρ。

三. 无进位基2加法与减法

基2有符号数位数字用两个无符号二进制数字编码，一个为正一个为负，$X=X^{+}-X^{-}$。因此，每个有符号数位用两个位表示，$x_i=x_i^{+}-x_i^{-}$，其中 x i + , x i − ∈ { 0 , 1 } x_i^+,x_i^-\in \{0,1\} xi+​,xi−​∈{0,1}且 x i ∈ { 1 ‾ , 0 , 1 } x_i\in \{\overline{1},0,1\} xi​∈{1,0,1}。本节考虑基2混合的和有符号数位的加法和减法。在混合操作中，一个输入操作数以及输出操作数是用冗余有符号数位表示法表示的，第二个输入操作数是普通的无符号数字。一个有符号数位加法可以看做是一个混合加法和一个混合减法的串联。

3.1 混合基2加法

考虑一个基2有符号数位数字和一个无符号普通数字的加法
$$S_{<2,1>}=X_{<2,1>}+Y$$
其中$X_{<r,a>}=x_{W-1}{x}_{W-2}...x_0,Y_{<b,a>}=y_{W-1}{y}_{W-2}...y_0$，且 x i ∈ { 1 ‾ , 0 , 1 } , y i ∈ { 0 , 1 } x_i\in \{\overline{1},0,1\},y_i\in \{0,1\} xi​∈{1,0,1},yi​∈{0,1}。这个加法用两步完成。

1. 第一步，以并行方式在所有位置$i(0\le i\le W-1)$上进行的。计算出中间和$p_i=x_i+y_i$，它的值在集合 { 1 ‾ , 0 , 1 , 2 } \{\overline{1},0,1,2\} {1,0,1,2}中。这个加法表示为
   $$x_i+y_i=(x_i^{+}-x_i^{-}+y_i^{+})=p_i=(2t_i^{+}-u_i^{-})=2t_i+u_i$$
   其中$t_i$是转移数位，值为$0$或$1$，记作$t_i^{+}$；$u_i$是临时和，值为$\overline{1}$或$0$，记作$-u_i^{-}$。最低的转移数位$t_{-1}$和最高的临时和数位$u_W$被置为0。
2. 第二步，将$t_{i-1}^{+}$和$u_i^{-}$组合成一个数位得到和的数位：
   $$s_i=s_i^{+}-s_i^{-}=t_{i-1}^{+}-u_i^{-}$$
   
   可以用加-加-减加法器(PPM)，实现8数位并行混合基2加法器结构。
   
   混合冗余加法也可以通过折叠用一个PPM加法器串行分时完成。
   

3.2 混合基2减法

考虑一个基2有符号数位数字和一个无符号普通数字的减法
$$S_{<2,1>}=X_{<2,1>}-Y$$
可以按照与混合加法相似方式完成。区别在于这里使用的是负的转移数位$t_i$。
3. 第一步，计算中间差$p_i=x_i-y_i$，它的值在集合 { 2 ‾ , 1 ‾ , 0 , 1 } \{\overline{2},\overline{1},0,1\} {2,1,0,1}中，用下式表示
$$x_i-y_i=(x_i^{+}-x_i^{-}-y_i^{-})=p_i=(-2t_i^{-}+u_i^{+})=2t_i+u_i$$
其中转移数位的值为$\overline{1}$或$0$，记作$-t_i^{-}$，临时差$u_i$的值为$0$或$1$，记作$u_i^{+}$。
4. 第二步，将$t_{i-1}^{-}$和$u_i^{+}$组合成一个数位得到和的数位：
$$s_i=s_i^{+}-s_i^{-}=-t_{i-1}^{-}+u_i^{-}$$

可以用减-减-加加法器(MMP)，实现8数位并行混合基2减法器结构。

3.3 混合基2加法减法器

混合加法减法器可以将一个有符号数位数字加上或减去一个无符号数字。混合减法可以通过混合加法完成，即被减数加上减数的2的补码（减数的相反数）并舍去最高数位上的进位输出。所以加法减法器可以同样的硬件实现。

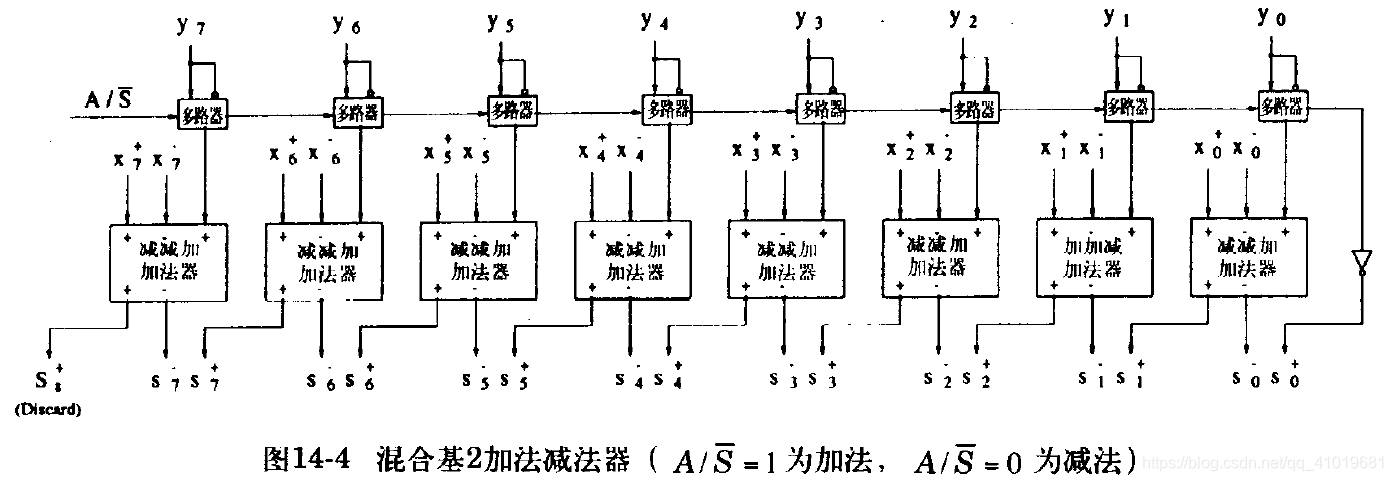
3.4 有符号二进制数位加法减法器

两个有符号数位加法可以通过进行一次混合加法和一次混合减法实现，如下所示：

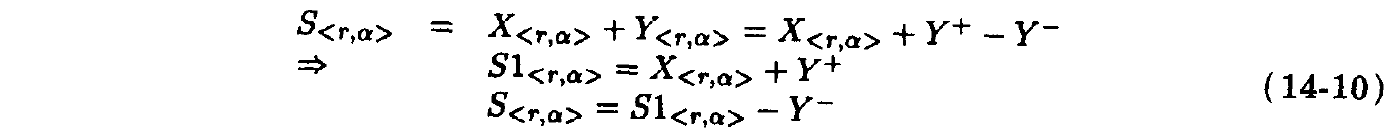
由于$-Y_{<2,1>}=Y^{-}-Y^{+}$，两个有符号数位减法可以通过交换减数的二进制数位码的正位和负位实现。

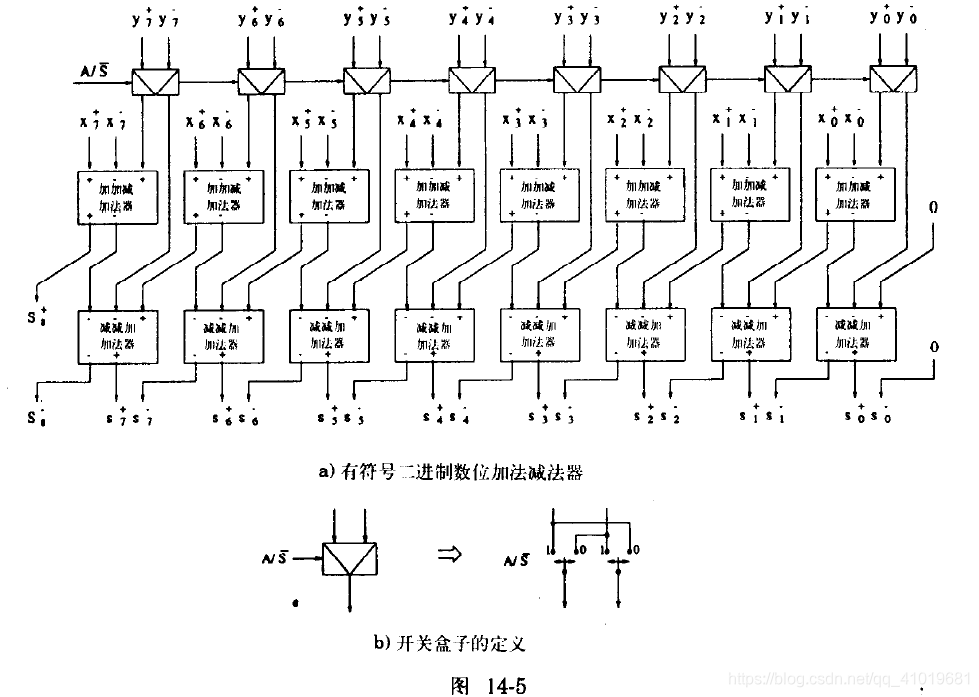
数位串行有符号二进制数位(SBD)加法器可以通过将数位并行加法器按最低数位优先或者最高数位优先的模式折叠得到。

四. 混合基4加法

基4因为所需要的迭代步数只是基2的一半而且实现并不比基2复杂许多，因而很有吸引力。基4冗余有符号数位集合可以是最大冗余，即基于数位集合$D_{<4,3>}$，也可以是最小冗余，即基于数位集合$D_{<4,2>}$。

4.1 最大冗余混合基4加法

最大冗余混合基4加法$S_{<4,3>}=X_{<4,3>}+Y_4$，其中数位$x_i、s_i\in D_{<4,3>},y_i\in D_4$的二进制码对应于两个连续的基2数位的带权加法。

1. 第一步，运算操作计算
   $$x_i+y_i=4t_i+u_i$$
   带入二进制码得到：
   $$(2x_i^{+2}-2x_i^{-2}+2y_i^{+2})+(x_i^{+}-x_i^{-}+y_i^{+})=4t_i^{+}+2u_i^{+2}-2u_i^{-2}-u_i^{-}$$
   
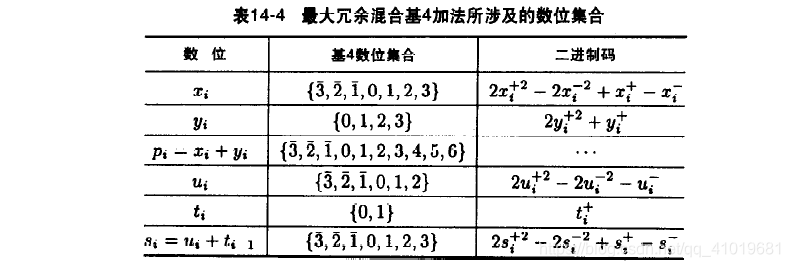
   使用最大冗余混合基4加法单元（MRHY4A）来完成上述的运算。这个单元含有两个PPM加法器，并行完成在括号内的两个加法，位数从6越减至4，权重由右端给出。
   
2. 第二步，混合加法算法由$s_i=u_i+t_{i-1}$给定。将$s_i、u_i、t_{i-1}$用相应的二进制码代替，得到$s_i^{+2}=u_i^{+2},s_i^{-2}=u_i^{-2},s_i^{+}=t_{i-1}^{+},s_i^{-}=u_i^{-}$。

混合基4加法器如下所示，W数位MRHY4A的结构与2W数位混合基2加法器完全相同。

4.2 最小冗余混合基4加法

最小冗余基4加法（mrHY4A）$S_{<4,2>}=X_{<4,2>}+Y_4$，其中数位$x_i$和$s_i\in D_{<4,2>}$的编码用3位表示，即一个权重为2的负位和两个权重为1的正位。

1. 第一步，运算操作计算
   $$x_i+y_i=4t_i+u_i$$
   带入二进制码得到：
   $$(-2x_i^{-2}+2y_i^{+2})+(x_i^{+}+x_i^{++}+y_i^{+})=4t_i^{+}-2u_i^{-2}+u_i^{+}$$
   
   mrHY4A单元由下图所示，其中一个全加器（FA）将三个权重为1的位（$x_i^{+}、x_i^{++}、y_i^{+}$）约减为两位（$u_i^{+}$和中间进位$c_i^{+2}$），接着一个PPM加法器将三个权重为2的位（$x_i^{-2}、y_i^{+2}$和$c_i^{+2}$）约减为两个新的位（$t_i^{+}$和$u_i^{-2}$）。
   
2. 第二步，利用$s_i^{-2}=u_i^{-2}、s_i^{+}=u_i^{+}、s_i^{++}=t_{i-1}^{+}$产生和的数位。mrHY4A的结构如下。
   

五. 基2混合冗余乘法架构（略）

六. 数据格式转换

6.1 非冗余到冗余转换

由于非冗余输入数位集合是冗余输入数位集合的子集，这个转换相对来说比较容易。

6.1.1 基2表示法

设非冗余数字$X$记为$X=x_3\cdot x_2{x}_1{x}_0$，相应的冗余表示记作$Y=y_3\cdot y_2{y}_1{y}_0$，其中每个数位$y_i$编码为$y_i^{+}-y_i^{-}$，而每个数位$x_i$表示1或0。注意在2的补码(2C)数字系统中位$x_3$的权重为-1。转换由下图表示。

6.1.2 基4表示法

七. 冗余到非冗余转换器（略）

7.1 最低数位优先转换（略）

7.2 最高数位优先转换（略）

八. 结论

本章给出了冗余数字系统和冗余运算的基本概念，从而得到了无进位加法的特性。本章还研究了混合基2和基4加减法器，以及有符号数加减法器的算法和架构。最后给出了非冗余到冗余的数据格式转换。