网络流： HDU 3338

HDU 3338

hdu 3338
Kakuro Extension
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2809 Accepted Submission(s): 971
Special Judge

Problem Description
If you solved problem like this, forget it.Because you need to use a completely different algorithm to solve the following one.
Kakuro puzzle is played on a grid of “black” and “white” cells. Apart from the top row and leftmost column which are entirely black, the grid has some amount of white cells which form “runs” and some amount of black cells. “Run” is a vertical or horizontal maximal one-lined block of adjacent white cells. Each row and column of the puzzle can contain more than one “run”. Every white cell belongs to exactly two runs — one horizontal and one vertical run. Each horizontal “run” always has a number in the black half-cell to its immediate left, and each vertical “run” always has a number in the black half-cell immediately above it. These numbers are located in “black” cells and are called “clues”.The rules of the puzzle are simple:

1.place a single digit from 1 to 9 in each “white” cell
2.for all runs, the sum of all digits in a “run” must match the clue associated with the “run”

Given the grid, your task is to find a solution for the puzzle.

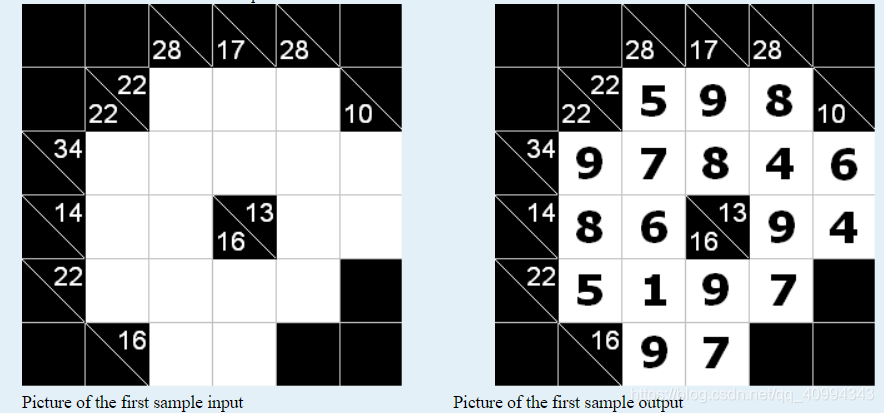
Sample Input

6 6
XXXXXXX XXXXXXX 028\XXX 017\XXX 028\XXX XXXXXXX
XXXXXXX 022\022 ....... ....... ....... 010\XXX
XXX\034 ....... ....... ....... ....... .......
XXX\014 ....... ....... 016\013 ....... .......
XXX\022 ....... ....... ....... ....... XXXXXXX
XXXXXXX XXX\016 ....... ....... XXXXXXX XXXXXXX
5 8
XXXXXXX 001\XXX 020\XXX 027\XXX 021\XXX 028\XXX 014\XXX 024\XXX
XXX\035 ....... ....... ....... ....... ....... ....... .......
XXXXXXX 007\034 ....... ....... ....... ....... ....... .......
XXX\043 ....... ....... ....... ....... ....... ....... .......
XXX\030 ....... ....... ....... ....... ....... ....... XXXXXXX

Sample Output

_ _ _ _ _ _
_ _ 5 8 9 _
_ 7 6 9 8 4
_ 6 8 _ 7 6
_ 9 2 7 4 _
_ _ 7 9 _ _
_ _ _ _ _ _ _ _
_ 1 9 9 1 1 8 6
_ _ 1 7 7 9 1 9
_ 1 3 9 9 9 3 9
_ 6 7 2 4 9 2 _

题意：给你一个n*m的矩阵，然后每个位置有一段长度为7的字符串，根据他对各个字符串的定义，会有一些要填入的总数和，有些是要计算出的总数和，有些是要你填的位置。他要求你填入一些数，使行和列的值的总和满足他给你要求的值，就是图中白色区域的行列值的和和黑色区域要求的值相等。

解题思路：据说这个是个很神奇的网络流，不过我的思路很常规，有一个处理的地方，因为他说填入的数的范围是[1,9]，而最大流无法规定下限，所以我们采取减1，取[0,8]的范围，最后再给他加上去就好了。大源点和大汇点，大源点向他提供的“源点”建一条流量为他要求的值的边，他提供的“汇点”向大汇点建一条流量为他要求的值的边。然后就是提供“源点”向要填入的数的点（空白点）建一条流量为8的边，空白点向提供“汇点”建一条流量为8的边。注意因为可能提供“汇点”和提供“源点”是同一个点，所以我们要拆一下点，虽然这个拆了点不是原来拆点的用处，只是为了让他变成两个不同的点，为了敲的方便，所以拆点了。。。。。然后就跑个最大流，再把流量输出就行了。

答案很多的原因：

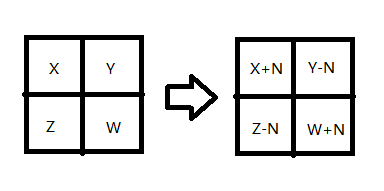
对答案是没有影响的

完整代码:

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <algorithm>
#include <queue>
using namespace std;
const int maxn=205;
const int inf=0x3f3f3f3f;
struct Edge{
    int u,v,c;
    int next;
}edge[maxn*maxn];
int n,m;
int edn;//边数
int head[maxn*maxn],dis[maxn*maxn];
int sp,tp;//原点，汇点

void addedge(int u,int v,int c)
{
    edge[edn].u=u; edge[edn].v=v; edge[edn].c=c;
    edge[edn].next=head[u]; head[u]=edn++;

    edge[edn].u=v; edge[edn].v=u; edge[edn].c=0;
    edge[edn].next=head[v]; head[v]=edn++;
}
int bfs()
{
    queue <int> q;
    memset(dis,-1,sizeof(dis));
    dis[sp]=0;
    q.push(sp);
    while(!q.empty())
    {
        int cur=q.front();
        q.pop();
        for(int i=head[cur];i!=-1;i=edge[i].next)
        {
            int u=edge[i].v;
            if(dis[u]==-1 && edge[i].c>0)
            {
                dis[u]=dis[cur]+1;
                q.push(u);
            }
        }
    }
    return dis[tp] != -1;
}
int dfs(int a,int b)
{
    int r=0;
    if(a==tp)return b;
    for(int i=head[a];i!=-1 && r<b;i=edge[i].next)
    {
        int u=edge[i].v;
        if(edge[i].c>0 && dis[u]==dis[a]+1)
        {
            int x=min(edge[i].c,b-r);
            x=dfs(u,x);
            r+=x;
            edge[i].c-=x;
            edge[i^1].c+=x;
        }
    }
    if(!r)dis[a]=-2;
    return r;
}

int dinic(int sp,int tp)
{
    int total=0,t;
    while(bfs())
    {
        while(t=dfs(sp,inf))
        total+=t;
    }
    return total;
}
int mp[105][105][3];
int main()
{
    int i,u,v,c;
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        edn=0;//初始化
        memset(head,-1,sizeof(head));
        memset(mp,0,sizeof(mp));
        for(int i=0;i<n;i++)
        {
            for(int j=0;j<m;j++)
            {
                char q[10];
                scanf("%s",q);
                if(q[3]=='X')
                {
                    mp[i][j][0]=-1;
                    continue;
                }else{
                    if(q[3]=='.')
                    {
                        mp[i][j][0]=1;
                        continue;
                    }
                    if(q[0]!='X')
                    {
                        mp[i][j][2]=(q[0]-'0')*100+(q[1]-'0')*10+(q[2]-'0');
                    }
                    if(q[4]!='X')
                    {
                        mp[i][j][1]=(q[4]-'0')*100+(q[5]-'0')*10+q[6]-'0';
                    }

                }
            }
        }
        sp=0,tp=n*m*2+1;
        for(int i=0;i<n;i++)
        {
            for(int j=0;j<m;j++)
            {
                if(mp[i][j][1]!=0)
                {

                    int k;
                    for(k=j+1;k<m;k++)
                    {
                        if(mp[i][k][0]==1)
                        {
                             addedge(i*m+j+1,i*m+k+1,8);//提供“源点”向空白点建边
                        }else{
                            break;
                        }
                    }
                    addedge(sp,i*m+j+1,mp[i][j][1]-(k-1-j));//大源点向提供“源点”建边
                }
                if(mp[i][j][2]!=0)
                {
                    int k;
                    for(k=i+1;k<n;k++)
                    {
                        if(mp[k][j][0]==1)
                        {
                            addedge(k*m+j+1,n*m+i*m+j+1,8);//空白点向提供“汇点”建边
                        }else
                            break;
                    }
                    addedge(n*m+i*m+j+1,tp,mp[i][j][2]-(k-1-i));//提供“汇点”向大汇点建边
                }
            }
        }
        int ans=dinic(sp,tp);
        for(int i=0;i<n;i++)
        {
            for(int j=0;j<m-1;j++)
            {
                if(mp[i][j][0]==1)
                {
                    for(int u=head[i*m+j+1];u!=-1;u=edge[u].next)
                    {
                        printf("%d ",edge[u].c+1);
                        break;
                    }
                }else{
                    printf("_ ");
                }
            }
            if(mp[i][m-1][0]==1)
            {
                    for(int u=head[i*m+m-1+1];u!=-1;u=edge[u].next)
                    {
                        printf("%d\n",edge[u].c+1);
                        break;
                    }
            }else{
                    printf("_\n");
            }
        }
    }


    return 0;
}