gym101982 B Coprime Integers （莫比乌斯）

链接：http://codeforces.com/gym/101982/attachments
题意：有两个区间[a，b]和[c，d]，求gcd(i，j)==1的对数，i$\in$[a，b]，j$\in$[c，d]

$和那种[1，a]和[1，b]两个区间求gcd(i，j)==1的对数的题目很类似。$
$在[1，a]和[1，b]两个区间求gcd(i，j)==1的问题中，$
$定义f(d)为gcd(i,j)==d的对数$
$定义g(n)为gcd(i,j)\%n==0的对数$
$这样就有了一个公式：g(n)=\sum (f(d))$ _n|d
$根据反演公式:F(n)=\sum (U(d/n)\ast G(d))$_n|d
$那么f(n)=\sum (u(d/n)\ast g(d))$_n|d
$求gcd==1，也就是求f(1)=\sum (u(d)\ast g(d))$_1|d
$反演的本质是一个未知的函数由一个已知的函数通过一些变化来得到，所以需要观察g(d)$
$g(d)为gcd(i,j)\%d==0的对数，也就是说i和j都是d的倍数，那么就看i有几个j有几个，相乘就是g(d)了$
$i和j的个数很显然就是上界/d，所以g(d)=(a/d)\ast (b/d)最后f(1)=\sum (u(d)\ast (a/d)\ast (b/d))$_1|d

到这里右边全部都是已知的，枚举下可取范围内的d（也就是原来n的倍数，这里n是1）
再回过来看看这道题，可以利用容斥原理，先求出[1，b]和[1，d]，再减去[1，a-1]和[1，d]以及[1，b]和[1，c-1]，最后加上多减的部分[1，a-1]和[1，c-1]。是不是有点像二维的前缀和求一个矩形的求法。

最后考虑下优化，这里求的gcd是1，也就是说范围内的每个数字都要枚举。$f(1)=\sum (u(d)\ast (a/d)\ast (b/d))$，观察发现当上界很大时，会有很长的一段区间[l，r]满足a/x的值相同，x$\in$[l，r]，这里(a/d)∗(b/d)的值是有两个区间合成的

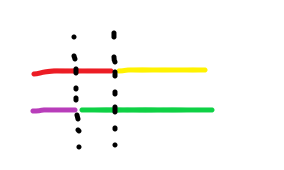
不同颜色表示不同的值，这样合成的不同值有三个，这个也是代码中左边界取min的意义。
如果现在有一段区间的(a/d)∗(b/d)值相同了，简单表示x=(a/d)∗(b/d)，那么这段区间的最终贡献为:x*∑u(l->r)，其中∑u(l->r)用前缀和维护下就可以O1得到，这个优化差不多是降ON为O根号N

参考代码：

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;

const int N=1e7+5;
const int maxn=1e7;
int mu[N],prime[N];
bool vis[N];
void work_mobius()
{
    mu[1]=1;
    int cnt=0;
    for(int i=2;i<=maxn;i++)
    {
        if(!vis[i])
        {
            prime[cnt++]=i;
            mu[i]=-1;
        }
        for(int j=0;j<cnt&&i*prime[j]<=maxn;j++)
        {
            vis[i*prime[j]]=true;
            if(i%prime[j]) mu[i*prime[j]]=-mu[i];
            else
            {
                mu[i*prime[j]]=0;
                break;
            }
        }
    }
    for(int i=2;i<=maxn;i++)
        mu[i]=mu[i-1]+mu[i];
}

ll solve(int b,int d){
    ll ret=0;
    for(int l=1,r=0;l<=min(b,d);l=r+1){
        r=min(b/(b/l),d/(d/l));//不理解的看看上面的图 (b/l)是第一个区间这段的值，b/(b/l)就变成这一段最右边的那个位置
        ret+=1ll*(mu[r]-mu[l-1])*(b/l)*(d/l);
    }
    return ret;
}


int main(){
    work_mobius();
    int a,b,c,d;
    scanf("%d%d%d%d",&a,&b,&c,&d);
    printf("%lld\n",solve(b,d)-solve(a-1,d)-solve(b,c-1)+solve(a-1,c-1));
    return 0;
}