664. 奇怪的打印机(动态规划)

664. 奇怪的打印机(动态规划)

有台奇怪的打印机有以下两个特殊要求：

• 打印机每次只能打印由 同一个字符 组成的序列。
• 每次可以在任意起始和结束位置打印新字符，并且会覆盖掉原来已有的字符。

给你一个字符串 s ，你的任务是计算这个打印机打印它需要的最少打印次数。

示例 1：

输入：s = "aaabbb"
输出：2
解释：首先打印 "aaa" 然后打印 "bbb"。

示例 2：

输入：s = "aba"
输出：2
解释：首先打印 "aaa" 然后在第二个位置打印 "b" 覆盖掉原来的字符 'a'。

提示：

• 1 <= s.length <= 100
• s 由小写英文字母组成

解法一、动态规划（区间dp）

1. ​ 定义子问题：

   分析 aba：

   (1) a子串 打印a 最少打印次数=1

   (2) ab子串 打印 aa 第二个用b覆盖 最少打印次数=2

   (3) aba串 打印aaa 中间b覆盖 最少打印次数=2 ps:增加的是a 与第一个字符相等，最少打印次数=（2）

可以看出当字符串长度变长时，最少最少打印次数与增加的这个字符息息相关。

那么有$dp[i,j]$,表示 $[i,j]$区间内的最少打印次数。

2. 分析$dp[i,j]$:

   • 初始化: 对于$dp[i][i]$，初始值为1，$[i,i]$打印一次。

   • 递推关系：对于字符串s，当$0<i<j<s.length()$:

     对于$dp[i][j]$: 若$s[i]==s[j]$,则说明打印机可以提前打印$s[j]$,这个状态可由一个子状态多打印一位而来。

     若$s[i]!=s[j]$,

     ​ 打印abab时，区间为$[0,3]$时（小于$[0,3]$的区间的$dp[i][j]$全部推出），$s[0]!=s[3]$ 需要会abab进行拆分，拆成aba，b 或 a， bab为最少打印数。

     则 遍历所有$[i,j]$中所有可能组合 ,取最小值，即： $dp[i][j]={\max }_{i<k<j}(dp[i][k]+dp[k][j])$

   • 总结有：
     

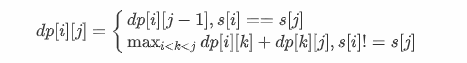
3. 确定递推公式计算顺序:

可以从公式中看到$s[i]!=s[j]$时，有取中间值k.此时$i<k<j$.

从前往后$dp[i][j]$时，j是小于i的，写起来要交换次序。故选择从后往前方便一些。

4. 空间优化:无

public int strangePrinter(String s) {
        int n = s.length();
        int[][] dp = new int[n][n];
        
        char[] words = s.toCharArray();
        
        //从后往前dp
        for(int i = n-1; i >= 0; --i){
            dp[i][i] = 1;  //初始化
            for(int j = i+1; j < n; ++j){
                if(words[i]==words[j]){
                    dp[i][j] = dp[i][j-1];
                }else{
                    int minn = Integer.MAX_VALUE;
                    for(int k = i; k < j; ++k){
                        minn= Math.min(minn, dp[i][k]+dp[k+1][j]);
                    }
                    dp[i][j] = minn;
                }
            }
        }
        return dp[0][n-1];
    }