[论文笔记]ACL-2021-Named Entity Recognition with Small Strongly Labeled and Large Weakly Labeled Data-优快云博客

该研究提出NEEDLE框架，解决NER任务中强标注数据不足、弱标注数据丰富的挑战。通过弱标签补全、噪音感知损失函数和强标签数据微调，有效抑制弱标签噪声，提升模型性能。在电商和生物医学领域实验中取得显著效果，尤其在生物医学NER数据集上刷新SoTa F1分数。

Named Entity Recognition with Small Strongly Labeled and Large Weakly Labeled Data

作者提出一个新的方法,用于解决强标注数据少,弱标注数据多的NER问题

动机

实际工程中,既有少量的强标注数据,又有大量的弱标注数据,直接组合或者加权组合这两种数据来训练NER模型,由于弱标签广泛的噪声,不一定能改善性能,甚至会影响模型性能

作者提出一个新的多阶段计算框架NEEDLE,主要包括①弱标签补全、②噪音感知损失函数、③强标签数据微调,通过电子商务和生物医学进行实验,证明了NEEDLE有效地抑制了弱标签的噪音，并在生物医学领域的3个NER数据集取得了新的SoTa F1分数

方法

0 符号定义

1. 给定一个N-Token的句子 $X=[x1,…,xN]\boldsymbol{X}=\left[x_{1}, \ldots, x_{N}\right]$ , 实体是一个多个token的span $s=[xi,…,xj](0≤i≤j≤N)\boldsymbol{s}=\left[x_{i}, \ldots, x_{j}\right](0 \leq i \leq j \leq N)$

使用BIO标注， $X$ 的真实标签为 $Y=[y1,…,yN]\boldsymbol{Y}=\left[y_{1}, \ldots, y_{N}\right]$

2. 给定M个已经标注好的句子作为强标签数据集$\left{\left(\boldsymbol{X}{m}, \boldsymbol{Y}{m}\right)\right}_{m=1}^{M} $, 用$ f(\boldsymbol{X} ; \theta)$来表示NER模型,训练模型可表示为

$θ^=argmin⁡θ1M∑m=1Mℓ(Ym,f(Xm;θ)) \widehat{\theta}=\underset{\theta}{\operatorname{argmin}} \frac{1}{M} \sum_{m=1}^{\mathrm{M}} \ell\left(\boldsymbol{Y}_{m}, f\left(\boldsymbol{X}_{m} ; \theta\right)\right)$
$ℓ(⋅,⋅)\ell(\cdot, \cdot)$ 是令牌式分类模型的交叉熵损失或CRF模型中的负似然函数

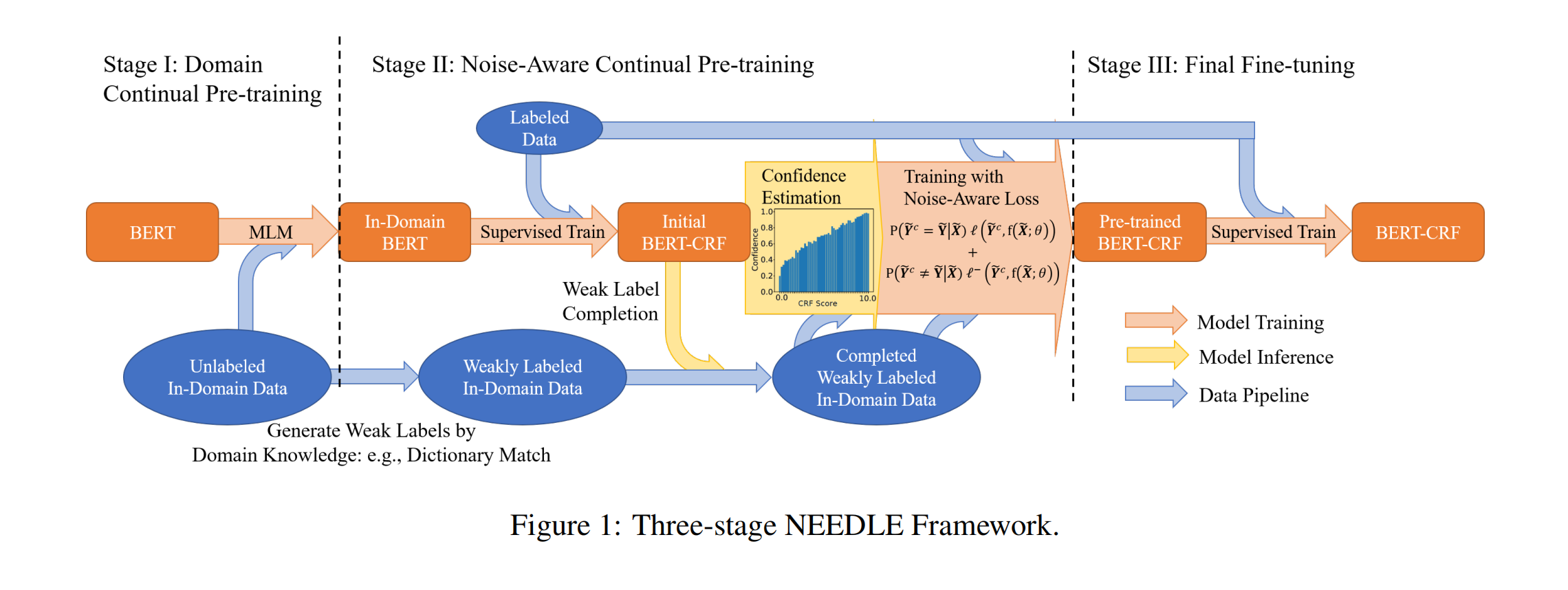
模型

总体设计

阶段1

使用未标注的域内数据进行持续预训练(MLM),模型会从朴素BERT变化为In-Domain BERT

阶段2

使用领域内的知识库通过弱监督的方式将无标签数据转换为弱标签的数据
对In-Domain BERT使用强标签数据进行有监督训练,得到Initial BERT-CRF
Weak Label Comletion:使用Initial BERT-CRF对弱标签数据进行一次预测,对弱标签中标签值为O的,使用预测结果进行补全。数学描述如下:
$y_{i}^{c}=\left\{\begin{array}{lr} y_{i}^{p} & y_{i}^{w}=O(\text { non }-\text { entity }) \\ y_{i}^{w} & \text { otherwise } \end{array}\right.$
- 对Initial BERT-CRF使用补全后的弱标签数据和强标签数据进一步训练,得到模型Pre-trained BERT-CRF
  $\begin{aligned} \min _{\theta} & \frac{1}{M+\widetilde{M}}\left[\sum_{m=1}^{M} \ell\left(\boldsymbol{Y}_{m}, f\left(\boldsymbol{X}_{m} ; \theta\right)\right)\right. \left.+\sum_{m=1}^{\widetilde{M}} \ell_{\mathrm{NA}}\left(\tilde{\boldsymbol{Y}}_{m}^{c}, f\left(\widetilde{\boldsymbol{X}}_{m} ; \theta\right)\right)\right] \end{aligned}$
  
  为解决模型过拟合到弱标签数据的噪声上,训练过程中使用作者全新设计的损失函数Noise-Aware Loss Function:主要思想是当我们对模型预测的一个实体的置信度较高时，我们就希望这个损失函数更“激进”一些，模型拟合得更多一些；置信度较低时，则希望模型拟合得更“保守”一些。

阶段3

对Pre-trained BERT-CRF使用强标签数据进行微调，获得最终模型BERT-CRF

Weak Label Comletion

为了缓解标签丢失问题

使用In-Domain BERT，对CRF进行随机初始化，获得模型 $)f\left(; \theta^{\text {Init }}\right)$ ，其中 $=\theta^{\text {Init }}=$ $(θenc,θCRF)\left(\theta_{\mathrm{enc}}, \theta_{\mathrm{CRF}}\right)$
给定一个弱标签集中的句子 $X~=[x1,…,xN]\widetilde{\boldsymbol{X}}=\left[x_{1}, \ldots, x_{N}\right]$ ，那么有原始弱标签 $Y~w=[y1w,…,yNw]\tilde{\boldsymbol{Y}}^{w}=\left[y_{1}^{w}, \ldots, y_{N}^{w}\right]$ ，以及模型预测结果 $))=[y1w,…,yNw]\tilde{\boldsymbol{Y}}^{p}=\operatorname{argmin}_{\boldsymbol{Y}} \ell\left(\boldsymbol{Y}, f\left(\widetilde{\boldsymbol{X}} ; \theta^{\text {Init }}\right)\right)=\left[y_{1}^{w}, \ldots, y_{N}^{w}\right]$
以原始弱标签的实体标注 $Y~w\tilde{\boldsymbol{Y}}^{w}$ 为主，但对于标注为non-entity的O标签,使用模型的预测结果 $Y~p\tilde{\boldsymbol{Y}}^{p}$ ,最终得到补全的弱标签标注序列 $Y~c=[y1c,…,yNc]\tilde{\boldsymbol{Y}}^{c}=\left[y_{1}^{c}, \ldots, y_{N}^{c}\right]$
$$
\begin{gathered}

y_{i}^{c}= \begin{cases}y_{i}^{p} & \text { if } y_{i}^{w}=0(\text { non-entity) } \
y_{i}^{w} & \text { otherwise }\end{cases}
\end{gathered}
$$

Noise-Aware Loss Function

为缓解模型过拟合弱标签数据的噪声

使用基于 $Y~c\tilde{\mathbf{Y}}^{c}$ 的置信度估计设计一个损失函数,

基于 $Y~c\tilde{\mathbf{Y}}^{c}$ 的置信度是指为 $Y~c\tilde{\mathbf{Y}}^{c}$ 为真实标签 $Y~\tilde{\mathbf{Y}}$ 的估计概率,即 $Y~:P^(Y~c=Y~∣X~)\tilde{\mathbf{Y}}: \widehat{P}\left(\tilde{\mathbf{Y}}^{c}=\tilde{\mathbf{Y}} \mid \widetilde{\mathbf{X}}\right)$ ,这个估计概率可以通过模型预测得分 $f(X~;θ)f(\widetilde{\mathbf{X}} ; \theta)$ 和直方图分档histogram binning进行估计,详见后面的cofidence Estimation专题
损失函数定义为:

$KaTeX parse error: No such environment: equation at position 12: { } \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ \begin{aligned…$

$P^(Y~c=Y~∣X~)\hat{P}\left(\widetilde{Y}^{c}=\tilde{Y} \mid \tilde{X}\right)$ : 置信度估计，也就是模型预测的弱标签等于其实际标的概率。

$P^(Y~c≠Y~∣X~)\hat{P}\left(\tilde{Y}^{c} \neq \tilde{Y} \mid \tilde{X}\right)$ : 表示的是模型预测的弱标签不等于其实际标签的概率。

$\left.\mathbf{1}\left(\widetilde{Y}{m}=\widetilde{Y}{m}^{c}\right)\right) $ : 是一个Indicator function，其含义是如果后面这个表达式为真,则值为 1否则为0

$ \ell(\boldsymbol{Y}, f(\boldsymbol{X} ; \theta))=-\log P_{f(\boldsymbol{X} ; \theta)}(\boldsymbol{Y}) $是负似然估计函数, 最小化$ \ell$的过程就是使得模型预测结果跟真实结果拟合的过程,

$ℓ−(Y,f(X;θ))=−log⁡[1−Pf(X;θ)(Y)]\ell^{-}(\boldsymbol{Y}, f(\boldsymbol{X} ; \theta))=-\log \left[1-P_{f(\boldsymbol{X} ; \theta)}(\boldsymbol{Y})\right]$ ,同理,最小化 $ℓ−\ell ^{-}$ 的过程就是使得模型预测结果跟真实结果偏离,

这个公式相当于是一个求期望的过程:

当 $Y^\hat{Y}$ 和 $Y^c\hat{Y}^{c}$ 相等时，取 $P^(Y~c=Y~∣X~)l(Y~c,f(X~;θ))\hat{P}\left(\widetilde{Y}^{c}=\widetilde{Y} \mid \widetilde{X}\right) l\left(\widetilde{Y}^{c}, f(\widetilde{X} ; \theta)\right)$ 作为损失;
当 $Y^\hat{Y}$ 和 $Y^c\hat{Y}^{c}$ 不等时，取 $P^(Y~c≠Y~∣X~)l−(Y~c,f(X~;θ))\hat{P}\left(\widetilde{Y}^{c} \neq \widetilde{Y} \mid \widetilde{X}\right) l^{-}\left(\widetilde{Y}^{c}, f(\widetilde{X} ; \theta)\right)$ 作为损失。

这就实现了"当我们对模型预测的一个实体的置信度较高时，我们就希望这个损失函数更“激进”一些，模型拟合得更多一些；置信度较低时，则希望模型拟合得更“保守”一些。"的初衷

置信度估计

假设补充完标签后的弱标签数据真正的golden标签是 $Y~\widetilde{Y}$ ,$ \hat{P}\left(\widetilde{Y}^{c}=\widetilde{Y} \mid \widetilde{X}\right)$ 的含义就是估计我们使用的 $Y~c\widetilde{Y}^{c}$ 为真实标签的概率。

置信度估计,简单的说就是评估补全后的弱标签 $Y~c\widetilde{Y}^{c}$ 的可靠程度。由前面可知, $Y~c\widetilde{Y}^{c}$ 由两部分组成，分别是原始的弱标签(利用知识库中知识通过规则转化来的) $Y~w\widetilde{Y}^{w}$ 和模型预测得到的标签(使用模型补全的) $Y~p\widetilde{Y}^{p}$ ，所以作者对这两部分的预测值进行求期望过程就得到了 $P^(Y~c=Y~∣X~)\hat{P}\left(\widetilde{Y}^{c}=\widetilde{Y} \mid \widetilde{X}\right)$ 的预测值。其计算公式如下:

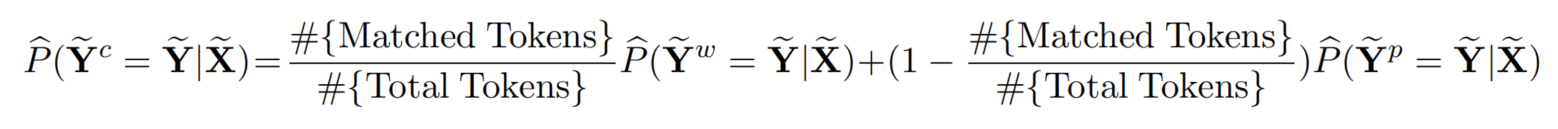
其中Total Tokens是一条句子的长度，而Matched Tokens 是其中标签不为 $O$ 的长度, $}\frac{\#\{\text { Matched Tokens }\}}{\#\{\text { Total Tokens }\}}$ 表示所有标签中弱标签预测的占比, $}1-\frac{\#\{\text { Matched Tokens }\}}{\#\{\text { Total Tokens }\}}$ 表示所有标签中基于模型补全的标签的占比。

令弱标签预测的置信度 $P^(Y~w=Y~∣X~)=1\hat{P}\left(\widetilde{Y}^{w}=\widetilde{Y} \mid \widetilde{X}\right)=1$ ，因为预测的标签都是基于领域的知识库匹配而来的，歧义更少
对于模型预测而补全的标签的置信度 $P^(Y~p=Y~∣X~)\hat{P}\left(\widetilde{Y}^{p}=\widetilde{Y} \mid \widetilde{X}\right)$ ,比较麻烦,采用模型校准的方法
1. 使用CRF模型求出最优序列,并获取最优序列对应的Score: $s (Y)$
  $\tilde{\mathbf{Y}}^{p}=\arg \max _{\mathbf{Y}} s(\mathbf{Y})=\operatorname{Decode}(\mathbf{Y}, f(\tilde{\mathbf{X}} ; \theta))$
2. 根据 $s (Y)$ 设置直方图分档
  
  就是对 $s (Y)$ 整个范围划分为n个bin,比如 $\in (3.16,5.31)$ 设置为一个bin
  
  对于每个bin使用一个小的验证集来计算 $模型预测正确的序列数验证集的总序列数\frac{\text{模型预测正确的序列数}}{验证集的总序列数}$ 作为置信度confidence,此时得到直方图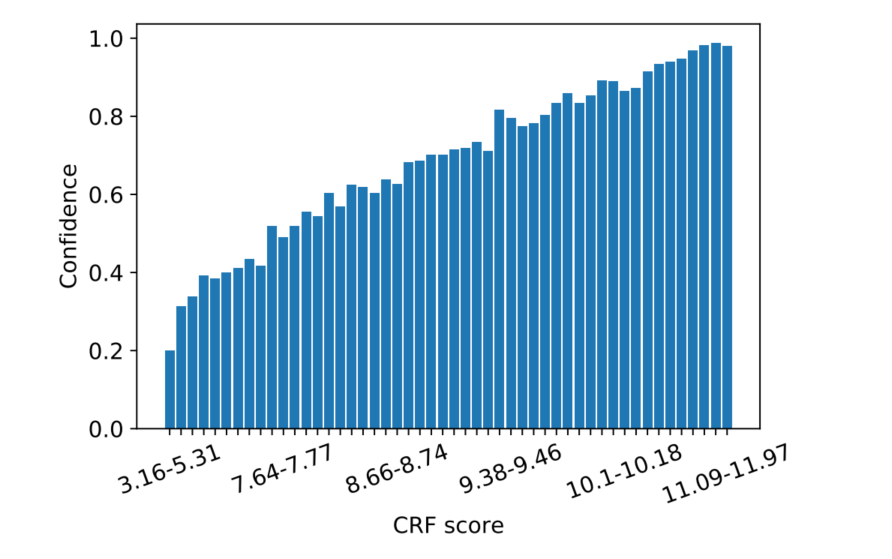
3. 对于每个样本,首先计算 $s (Y)$ ,然后通过上图找到对应的bin的置信度confidence,作为估计预测的置信度 $P^(Y~p=Y~∣X~)=confidence\hat{P}\left(\widetilde{Y}^{p}=\widetilde{Y} \mid \widetilde{X}\right) = confidence$
最终,强制平滑函数来进行保守的估计
$P\left(\tilde{\mathbf{Y}}^{c}=\tilde{\mathbf{Y}} \mid \tilde{\mathbf{X}}\right)=\min \left(0.95, P\left(\tilde{\mathbf{Y}}^{c}=\tilde{\mathbf{Y}} \mid \tilde{\mathbf{X}}\right)\right)$
强制执行这样的平滑来计算任何潜在的错误（例如，不准确的原始弱标签），并防止模型过拟合。平滑参数固定为0.95