李宏毅《机器学习》| 回归

最新推荐文章于 2025-05-15 07:55:33 发布

哒卜琉歪歪

最新推荐文章于 2025-05-15 07:55:33 发布

阅读量355

点赞数 2

文章标签：机器学习回归人工智能

本文链接：https://blog.youkuaiyun.com/qq_40857571/article/details/122461655

版权

一、定义

二、模型步骤

step1：模型假设，选择模型框架(线性模型)

1. 一元线性模型

2. 多元线性模型

step2：模型评估，判断模型的好坏(损失函数)

step3：模型优化，筛选最优的模型(梯度下降)

梯度下降(Gradient Descent)

step3：加入正则化项(Regularization)

一、定义

输入特征 x，通过找到的函数function输出数值Scalar

应用举例：

股市预测（Stock market forecast）
- 输入：过去10年股票的变动、新闻咨询、公司并购咨询等
- 输出：预测股市明天的平均值
自动驾驶（Self-driving Car）
- 输入：无人车上的各个sensor的数据，例如路况、测出的车距等
- 输出：方向盘的角度
商品推荐（Recommendation）
- 输入：商品A的特性，商品B的特性
- 输出：购买商品B的可能性
Pokemon精灵攻击力预测（Combat Power of a pokemon）：
- 输入：进化前的CP值、物种（Bulbasaur）、血量（HP）、重量（Weight）、高度（Height）
- 输出：进化后的CP值
- 下面的模型也以该例为基础进行展示

二、模型步骤

step1：模型假设，选择模型框架(线性模型)

1. 一元线性模型

即模型为单个输入特征，线性模型假设为 $y=b+\omega *x$

2. 多元线性模型

即模型为多个输入特征，线性模型假设为 $y=b+\sum \omega_{i} *x_{i}$

其中 $x_{i}$ 表示输入的多个特征， $\omega _{i}$ 表示各输入特征的权重，b表示偏移量

图中 $x^{1}$ 为进化前的CP值， $y\hat{}^{1}$ 表进化后的CP值，即输出的Scalar， $hat{}$ 所代表的是真实值

上图为10组数据在二维图中的展示，每一个点代表输入进化前的CP值和进化后的CP值

step2：模型评估，判断模型的好坏(损失函数)

我们可以将损失函数(Loss Function)理解成函数的函数，输入的是一个function，输出的是该function不好的程度。对于本例，使用距离即计算进化后的CP值与模型预测的CP值之间的的差值来判定模型的好坏，即计算 $\left ( y\hat{}^{n}-f(x_{cp}^{n}) \right )^{2}$ 的和，和越小，该模型越好。

$\omega$ 和b $b$ 在二维坐标图中的情况如下图所示，图中每一个点代表一个function，颜色代表根据所定义的损失函数该function效果好坏的程度。点所处的区域颜色越红越靠近图片下方，代表代表该function的效果越差。

step3：模型优化，筛选最优的模型(梯度下降)

最终需要找到使得损失函数 $L$ 的值达到最小的 $f^{*}$ ，下图展示的即为该模型中的最优化问题。

我们使用梯度下降法(Gradient Descent)求解该问题，该方法的优点在于只要损失函数 $L$ 可微分，则该问题就可求解。

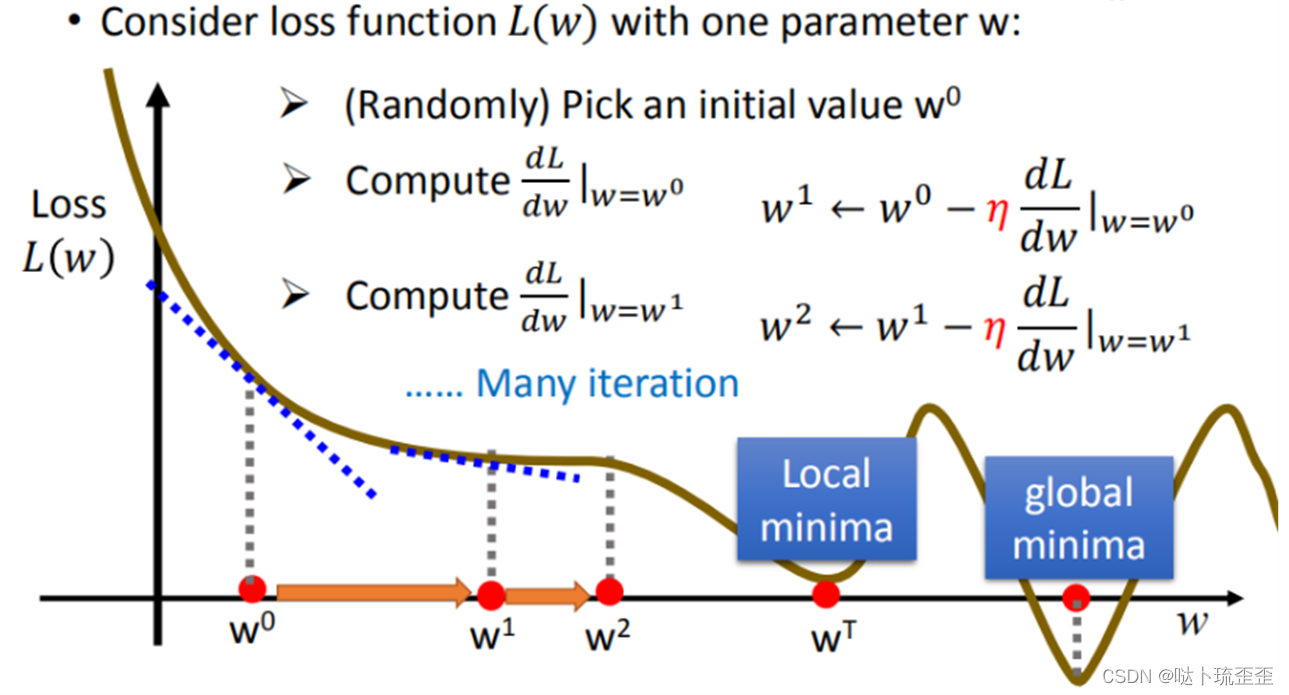
梯度下降(Gradient Descent)

先从最简单的只有一个参数 $\omega$ 入手，定义 $\omega =arg\mathop {\min }\limits_\omega L(\omega )$

穷举 $\omega$ 所有可能值，并代入损失函数 $L$ 中求不同 $\omega$ 下的损失。随机选取一个初始的 $\omega ^{0}$ ，计算 $L$ 在 $\omega =\omega ^{0}$ 时的微分（即切线斜率），若小于0（即图中所示情况），说明 $\omega ^{0}$ 左边的损失较高，右边损失较低，我们需要寻找使得损失函数 $L$ 达到最小的 $\omega$ ，所以此时应该增大 $\omega$ 的值；反之，应减小 $\omega$ 的值。

寻找下一个 $\omega$ 时应该增大或减小的量取决于两个因素，一个是 $L$ 在 $\omega =\omega ^{0}$ 时微分的大小，微分的绝对值越大，代表该点损失函数 $L$ 的值越大，切线越陡峭，则“迈出的步长”也应该越大；另一个是事先指定的常数项 $\eta$ ，即学习率(Learning Rate)， $\eta$ 越大，则“迈出的步长”的幅度即参数更新的幅度越大，学习的速度就越快。