(二叉树DFS)天平UVa 839

题目

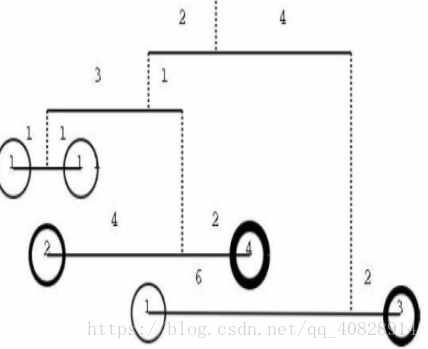
输入一个树状天平，根据力矩相等原则判断是否平衡。如图6-5所示，所谓力矩相等，就是WlDl=WrDr，其中Wl和Wr分别为左右两边砝码的重量，D为距离。采用递归（先序）方式输入：每个天平的格式为Wl，Dl，Wr，Dr，当Wl或Wr为0时，表示该“砝码”实际是一个子天平，接下来会描述这个子天平。当Wl=Wr=0时，会先描述左子天平，然后是右子天平。

样例输入：

1
0 2 0 4
0 3 0 1
1 1 1 1
2 4 4 2
1 6 3 2

输出
YES

分析与解答

刘汝佳说要完全理解这个程序，那我就把递归过程写了一下

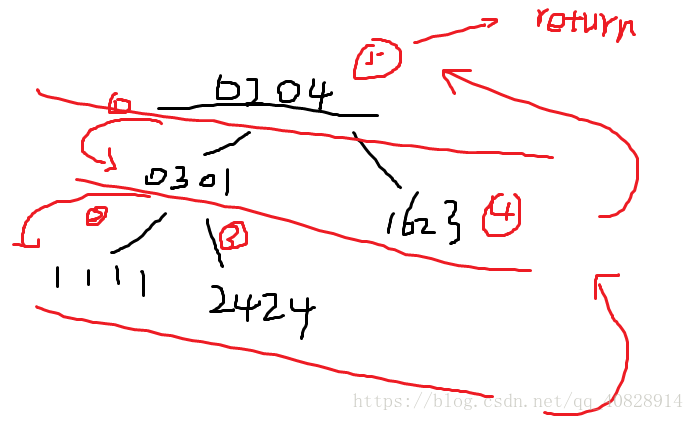
输入采用先序，并且输入顺序刚好就是递归的顺序，那就可以在输入过程进行判断
对每个结点判断，如果有子节点，那么就要判断左右子树是否平衡，以及这个树本身是否平衡，b1为true说明左子树平衡，b2右子树，w1是左边子天平所有砝码的总重量，w2右边。（w1*d1==w2*d2）说明这个树平衡。由于solv函数采用传引用方式，所以，每次那一层的函数返回时，w1和w2都已经分别赋为那个子树所有