个人项目数独

一 项目地址

二 PSP

三 解题思路

四 设计实现过程

五 代码说明

一 项目地址

代码托管在了GitHub上，地址：https://github.com/lll1230/sudoku

二 PSP

 

三 解题思路

   要写一个求解数独的程序，必须要线弄清楚要用什么方法去求解数独。一般是采取简单的摒除法，然而事实上摒除法并不能做比较高级的数独。深究下去发现较高级的数独可用的方法多达十种，而且面对不同的数独要运用不同的方法，相应的算法打码量十分庞大，而且并没有一个一定的套路。计算机擅长重复单调工作，为了程序能更好的设计，我考虑使用候选数法，在候选数法不能得到解的时候采取搜索的方法，这样能保证一定的性能下一定能求出一个数独的解。数独要求每行每列相邻位置的数不能一样，同时，每行每列一种数字只出现一次。

查看文档 

http://blog.sina.com.cn/s/blog_a28e3dd90101e1i2.html

http://www.cnblogs.com/Aria-K-Alethia/p/7593964.html

https://en .wikipedia.org/wiki/Sudoku_solving_algorithms

http://www.runoob.com/w3cnote/git-guide.html

  1、每个格子都填入了数字；

    2、每一行都要有1~9这9个数字填入；

    3、每一列都要有1~9这9个数字填入；

    4、每一块都要有1~9这9个数字填入。

    所以，01模型中列的定义就出来了。

    （i，j，k表示在棋盘上i行j列填入数字k。）

    1到81，表示棋盘中9*9=81个格子是否填入了数字。如果是，则选取的01行在该01列上有1。

    对应的01列编号为：(i-1)*9+j。

    81+1到81*2，表示棋盘中9行，每行的9个不同的数字是否填入。棋盘上某行已经填入了某个数字，则在选取

    的01行上， 对应的01列有1。

    对应的01列编号为：81+(i-1)*9+k

    81*2+1到81*3，表示棋盘中9列，每列的9个不同的数字是否填入。

    对应的01列编号为：81*2+(j-1)*9+k

    81*3+1到81*4，表示棋盘中9块，每块的9个不同的数字是否填入。

    01行是状态。数独做完后的状态是什么，就是棋盘上每个格子填入的究竟是什么数字。

    所以，01行表示的是，棋盘上某个格子填入的是什么数字

    那01行的行数就是9*9*9。

    每01行，既在棋盘中某个格子填入一个数字，会影响01矩阵的那些01列呢。

四 设计实现过程

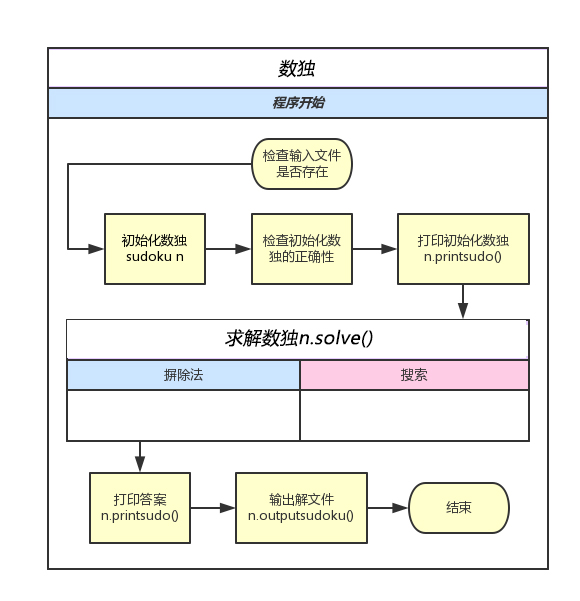
主要流程

这里主要涉及两个功能，一个是摒除法，一个是搜索。 
那么这里是先使用摒除法，如果摒除法不可继续求解的时候使用搜索，搜索之后使用摒除法探求正确性，一旦有错回溯并搜索下一个可能解。 

这是程序的大致框架：

五 代码说明

主要功能

采用分离实现和接口的方式。

为了能更好的计算候选数，同时不给原来的数独带来麻烦，我设计两个数组：一个是用来记录数独的，一个是用来记录候选数的。 
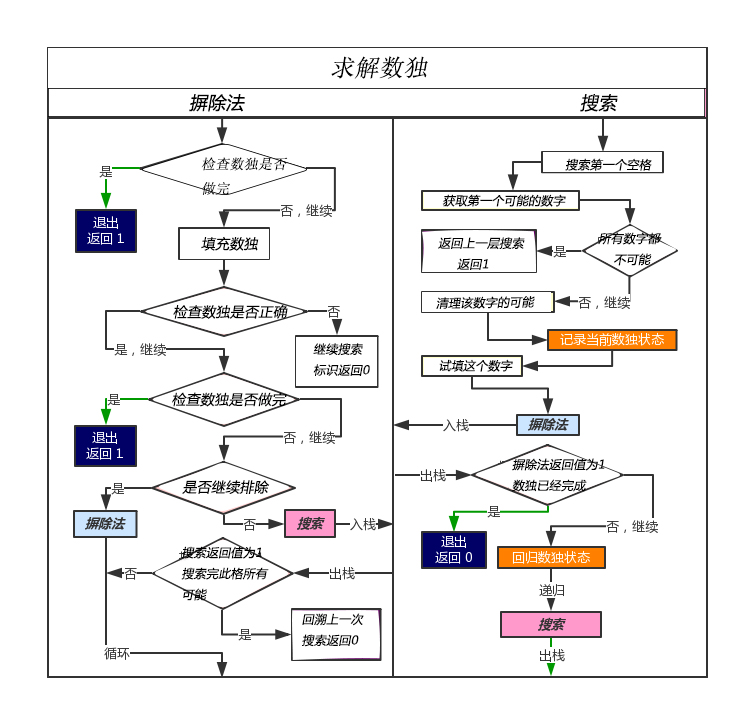
填充数独的时候先使用摒除法 base_solve() ，首先删除不可能的候选数 clear_solv_sudoku(int, int, int) ，然后填写唯一候选数到数独 update_ques_sudoku() 。然后在不能继续摒除的时候使用搜索 search() 。 

总体程序框架如下

功能实现

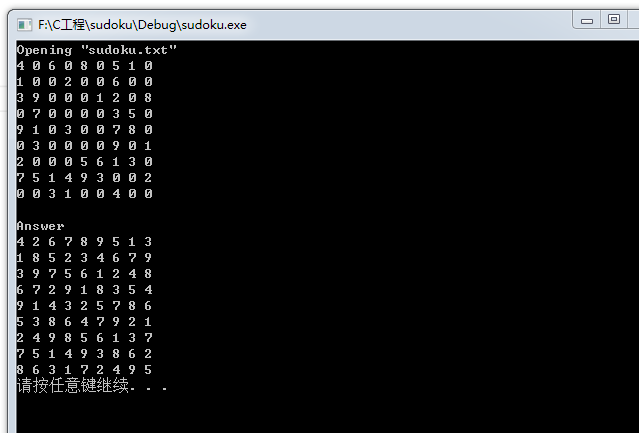
程序测试结果：

总结

通过这一次软件工程个人项目，了解到了自己的不足，看到了自己代码编程能力的薄弱，也学到了GitHub

以后继续努力