目录:
1、硬间隔
(1)SVM-统计学习基础
最小间距超平面:所有样本到平面的距离最小。而距离度量有了函数间隔和几何间隔,函数间隔与法向量 w w w和 b b b有关, w w w变为 2 w 2w 2w则函数间距变大了,于是提出了几何距离,就是对 w w w处理,除以 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣,除以向量长度,从而让几何距离不受影响。
但是支持向量机提出了最大间隔分离超平面,这似乎与上面的分析相反,其实这个最大间隔是个什么概念呢?通过公式来分析一下,正常我们假设超平面公式是:
w
T
x
+
b
=
0
/
/
超
平
面
w^{T}x+b=0 // 超平面
wTx+b=0//超平面
max
w
,
b
γ
s
.
t
.
y
i
(
w
∣
∣
w
∣
∣
x
i
+
b
∣
∣
w
∣
∣
)
>
γ
\max \limits_{w,b} \quad \gamma \ s.t. \quad y_i(\frac{w}{||w||}x_i+\frac{b}{||w||}) > \gamma
w,bmaxγ s.t.yi(∣∣w∣∣wxi+∣∣w∣∣b)>γ 也就是说对于所有的样本到超平面距离 都大于
γ
\gamma
γ,那这个
γ
\gamma
γ如何求解,文中约定了概念支持向量:正负样本最近的两个点,这两个点之间的距离就是
γ
\gamma
γ,那么问题来了,这中间的超平面有无数个,如何确定这个超平面呢?于是我们可以约束这个超平面到两个最近的点的距离是一样的。
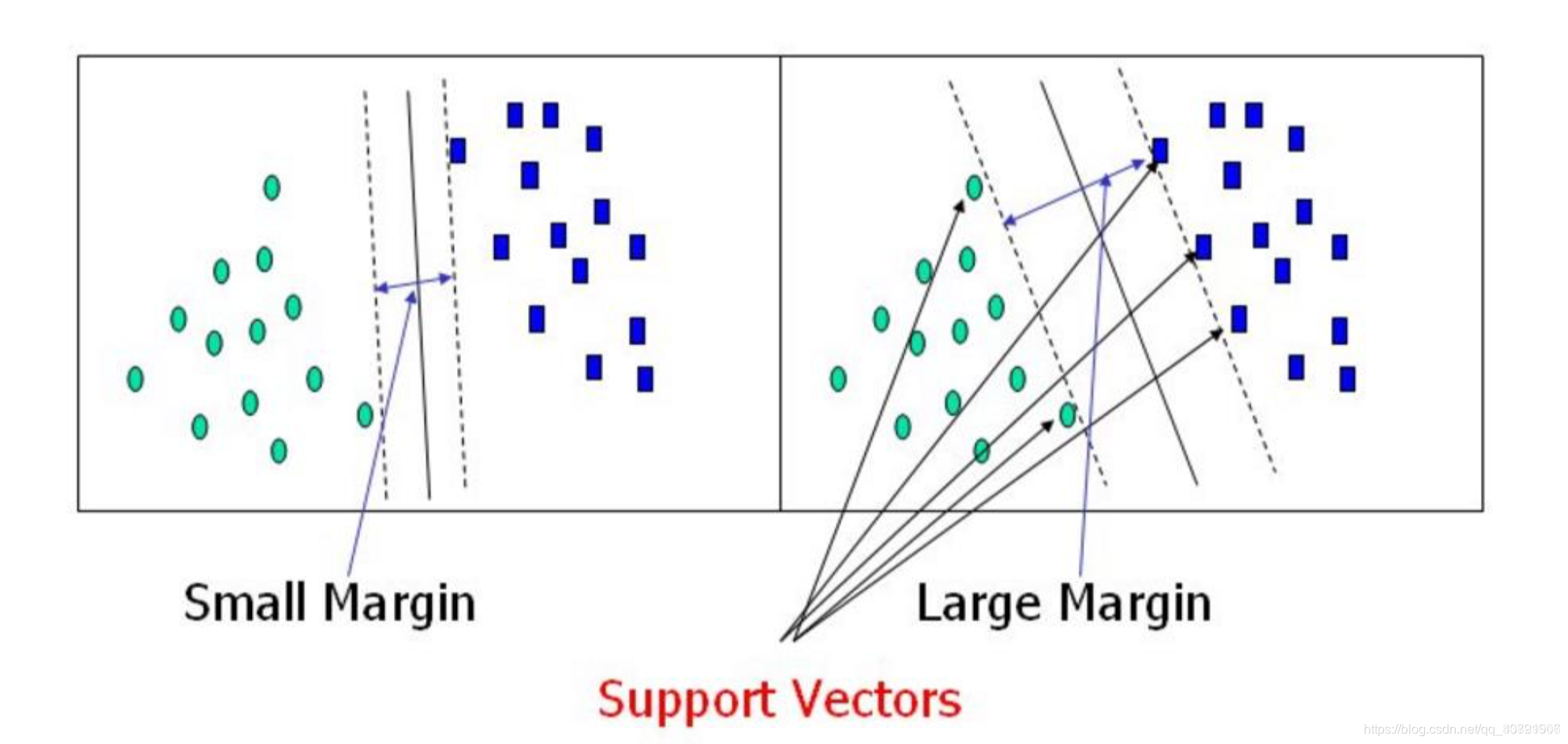
以上右图中两个绿色圆形点与三个蓝色方形点就是支持向量,通过这个求解目标,以及约束条件来求解这个超平面。书中有完整的公式装换以及证明这个超平面的唯一性。
这里要讲解一个样本点到直线的距离, 正常我们可能难以理解公式里
y
y
y去哪里了,拿二维空间做例子,正常我们说一个线性方程都是
y
=
a
x
+
b
y=ax+b
y=ax+b,其中a和b都是常量,这个线性方程中有两个变量
x
x
x和
y
y
y,转换公式就是
y
−
a
x
−
b
=
0
y-ax-b=0
y−ax−b=0,从线性矩阵的角度来思考问题就是
y
y
y是
x
1
x_1
x1,
x
x
x是
x
2
x_2
x2,用一个
w
T
w^T
wT来表示这两者的系数,用
b
b
b代替
−
b
-b
−b,所以公式就变为了:
w
T
x
+
b
=
0
w^{T}x+b=0
wTx+b=0 于是任意一个样本点到超平面的距离是:
r
=
∣
w
T
x
+
b
∣
∣
∣
w
∣
∣
r = \frac{|w^{T}x+b|}{||w||}
r=∣∣w∣∣∣wTx+b∣ 也就是说约束条件中要求
>
γ
>\gamma
>γ,其实就是大于支持向量到超平面的距离。
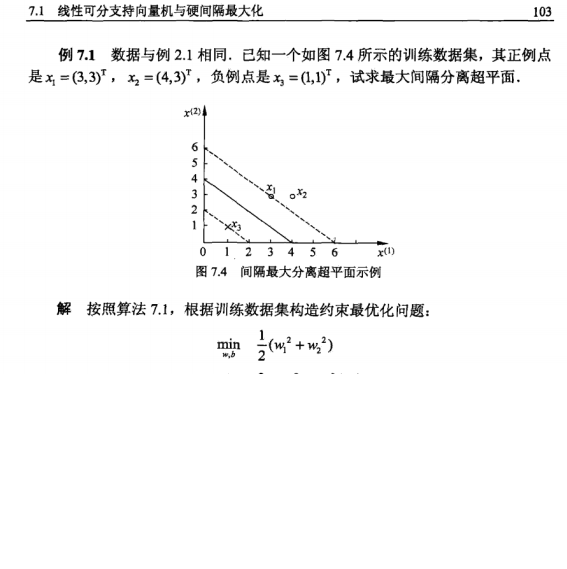
通过一个例子来看看: 这里例子中有
w
1
,
w
2
w_1,w_2
w1,w2,这是因为坐标点是二维的,相当于样本特征是两个,分类的结果是这两个特征的结果标签,所以这里的
w
w
w就是一个二维的,说明在具体的应用里需要根据特征来确定
w
w
w的维度。
(2)对偶讲解
①转化对偶问题
我们的目标函数:
(1)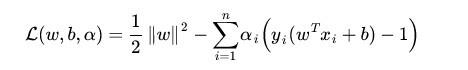
我们在优化时喜欢求最小值,将上式转化正等价的求最小值如下:
(2)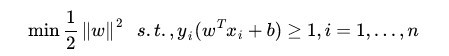
对于(2)式,这是一个凸二次规划问题,我们可以使用拉格朗日乘数法进行优化。
(3)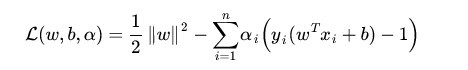
(3)式中的是拉格朗日乘子,然后我们令:
(4)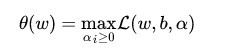
为什么能这样假设呢?如果约束条件都满足,(4)式的最优值就是,和目标函数一样。
因此我们可以直接求(4)式的最小值,等价于求原目标函数。因此目标函数变成如下:
(5)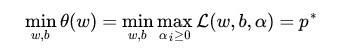
将求最大值和最小值交换位置后
(6)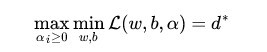
交换以后的新问题是原始问题的对偶问题,这个新问题的最优值用来表示。而且有d≤p,在满足某些条件的情况下,这两者相等,这个时候就可以通过求解对偶问题来间接地求解原始问题。为什么要这样转换呢?此处借他人之言,之所以从minmax的原始问题,转化为maxmin的对偶问题,一者因为是的近似解,二者,转化为对偶问题后,更容易求解。下面可以先求L 对w、b的极小,再求L 对的极大。
②求解对偶问题
回顾一下上面的目标函数L
(7)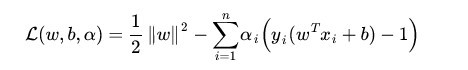
这是一个拉格朗日乘法优化方法得到的,由于要求
(8)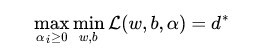
先求最大值,后求最小值,求最小值时,将a看成常量,那么L就是w,b的函数了。极值在导数为0的点处取到,因此分
别求L对w,b的导数,并令其为0,得如下结果。
(9)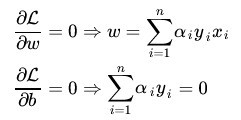
将(9)式带入(7)(为什么呢?)得到:
(10)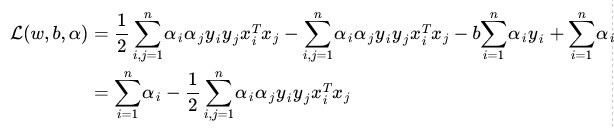
为什么能将(9)式带入(7)式呢?因为极值在导数为零的点处取到,因此(9)式符合(7)式取极值时w,b的取值。(10)式就是(7)式的最小值了,求完最小值,然后求最大值。求对的极大,即是关于对偶问题的最优化问题。经过上面第一个步骤的求w和b,得到的拉格朗日函数式子已经没有了变量w,b,只有。从上面的式子得到:
(11)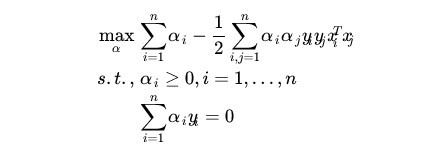
(11)式是关于a的式子,如果能求出a,则可以根据(7)式求出w。求出w后可以根据前面函数距离等于1的假设求出b
怎样求a呢?这需要后面的核函数和松弛量的知识,利用SMO算法求解。
最后附一张手写推导图,是上面内容的简化版本。

2.软间隔
硬间隔是方便用来分隔线性可分的数据,如果样本中的数据是线性不可分的呢?也就是如图所示: 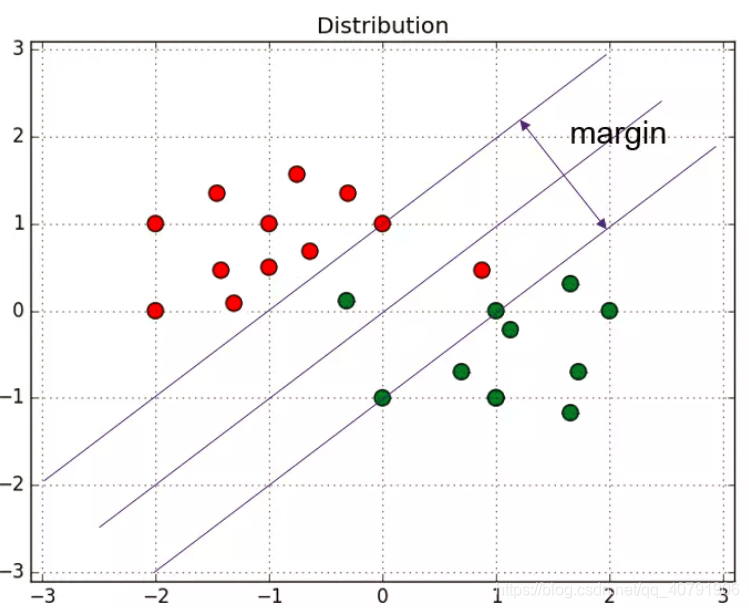
有一部分红色点在绿色点那边,绿色点也有一部分在红色点那边,所以就不满足上述的约束条件:
s
.
t
.
y
i
(
x
i
+
b
)
>
1
s.t. \quad y_i(x_i+b) >1
s.t.yi(xi+b)>1,软间隔的最基本含义同硬间隔比较区别在于允许某些样本点不满足原约束,从直观上来说,也就是“包容”了那些不满足原约束的点。软间隔对约束条件进行改造,迫使某些不满足约束条件的点作为损失函数,如图所示:

软间隔公式 这里要区别非线性情况,非线性的意思就是一个圆圈,圆圈里是一个分类结果,圆圈外是一个分类结果。这就是非线性的情况。
其中当样本点不满足约束条件时,损失是有的,但是满足条件的样本都会被置为0,这是因为加入了转换函数,使得求解min的条件会专注在不符合条件的样本节点上。
但截图中的损失函数非凸、非连续,数学性质不好,不易直接求解,我们用其他一些函数来代替它,叫做替代损失函数(surrogate loss)。后面采取了松弛变量的方式,来使得某些样本可以不满足约束条件。
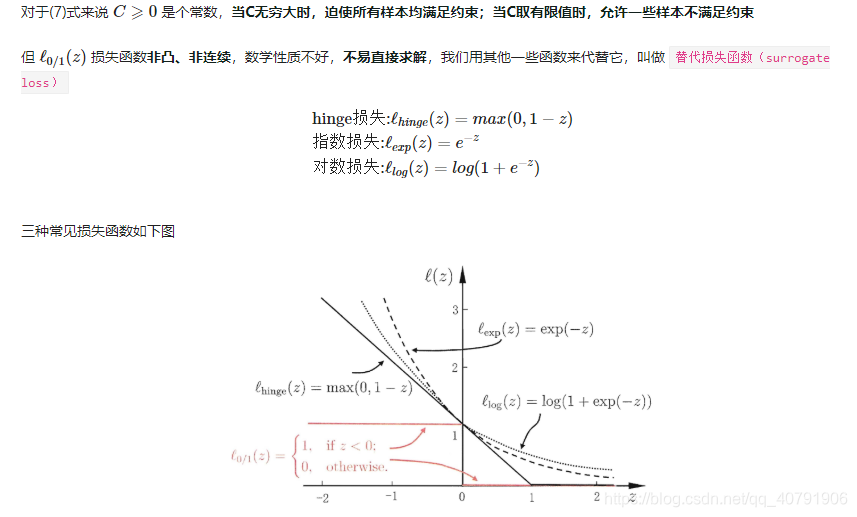
这里思考一个问题:既然是线性不可分,难道最后求出来的支持向量就不是直线?某种意义上的直线? 其实还是直线,不满足条件的节点也被错误的分配了,只是尽可能的求解最大间隔,
3.核函数
引入核函数可以解决非线性的情况:将样本从原始空间映射到一个更高为的特征空间,使得样本在这个特征空间内线性可分。图片所示:

粉红色平面就是超平面,椭圆形空间曲面就是映射到高维空间后的样本分布情况,为了将样本转换空间或者映射到高维空间,我们可以引用一个映射函数,将样本点映射后再得到超平面。这个技巧不仅用在SVM中,也可以用到其他统计任务。 但映射函数并不是最重要的,核函数是重要的,看到《统计学习方法》中提到的概念: 
其中映射函数与核函数之间有函数关系,一般我们显示的定义核函数,而不显示的定义映射函数,一方面是因为计算核函数比映射函数简单,我们对一个二维空间做映射,选择的新空间是原始空间的所有一阶和二阶的组合,得到了五个维度;如果原始空间是三维,那么我们会得到 19 维的新空间,这个数目是呈爆炸性增长的,这给 的计算带来了非常大的困难,而且如果遇到无穷维的情况,就根本无从计算了。所以就需要 Kernel 出马了。这样,一个确定的核函数,都不能确定特征空间和映射函数,同样确定了一个特征空间,其映射函数也可能是不一样的。举个例子:

上述例子很好说明了核函数和映射函数之间的关系。这就是核技巧,将原本需要确定映射函数的问题转换为了另一个问题,从而减少了计算量,也达到了线性可分的目的,
原始方法: 样本X ----> 特征空间Z ---- > 内积求解超平面
核函数: 样本X ---- > 核函数 求解超平面
但是我一直很疑惑,为什么这个核函数就正好是映射函数的内积?他为什么就可以生效?核函数的参数是哪里来的?就是样本中的两个样本点 ? 查看了一些博客之后,慢慢理解,得到以下的内容。 
这也说明核函数是作用在两个样本点上的,
最理想的情况下,我们希望知道数据的具体形状和分布,从而得到一个刚好可以将数据映射成线性可分的 ϕ(⋅) ,然后通过这个 ϕ(⋅) 得出对应的 κ(⋅,⋅) 进行内积计算。然而,第二步通常是非常困难甚至完全没法做的。不过,由于第一步也是几乎无法做到,因为对于任意的数据分析其形状找到合适的映射本身就不是什么容易的事情,所以,人们通常都是“胡乱”选择映射的,所以,根本没有必要精确地找出对应于映射的那个核函数,而只需要“胡乱”选择一个核函数即可——我们知道它对应了某个映射,虽然我们不知道这个映射具体是什么。由于我们的计算只需要核函数即可,所以我们也并不关心也没有必要求出所对应的映射的具体形式。
常用的核函数及对比:
Linear Kernel 线性核
k
(
x
i
,
x
j
)
=
x
i
T
x
j
k(x_i,x_j)=x_i^{T}x_j
k(xi,xj)=xiTxj 线性核函数是最简单的核函数,主要用于线性可分,它在原始空间中寻找最优线性分类器,具有参数少速度快的优势。 如果我们将线性核函数应用在KPCA中,我们会发现,推导之后和原始PCA算法一模一样,这只是线性核函数偶尔会出现等价的形式罢了。
Polynomial Kernel 多项式核 k ( x i , y j ) = ( x i T x j ) d k(x_i,y_j)=(x_i^{T}x_j)^d k(xi,yj)=(xiTxj)d 也有复杂的形式: k ( x i , x j ) = ( a x i T x j + b ) d k(x_i,x_j)=(ax_i^{T}x_j+b)^d k(xi,xj)=(axiTxj+b)d 其中 d ≥ 1 d\ge1 d≥1为多项式次数,参数就变多了,多项式核实一种非标准核函数,它非常适合于正交归一化后的数据,多项式核函数属于全局核函数,可以实现低维的输入空间映射到高维的特征空间。其中参数d越大,映射的维度越高,和矩阵的元素值越大。故易出现过拟合现象。
径向基函数 高斯核函数 Radial Basis Function(RBF)
k ( x i , x j ) = e x p ( − ∣ ∣ x i − x j ∣ ∣ 2 2 σ 2 ) k(x_i,x_j)=exp(-\frac{||x_i-x_j||^2}{2\sigma^2}) k(xi,xj)=exp(−2σ2∣∣xi−xj∣∣2)
σ > 0 \sigma>0 σ>0是高斯核带宽,这是一种经典的鲁棒径向基核,即高斯核函数,鲁棒径向基核对于数据中的噪音有着较好的抗干扰能力,其参数决定了函数作用范围,超过了这个范围,数据的作用就“基本消失”。高斯核函数是这一族核函数的优秀代表,也是必须尝试的核函数。对于大样本和小样本都具有比较好的性能,因此在多数情况下不知道使用什么核函数,优先选择径向基核函数。
Laplacian Kernel 拉普拉斯核 k ( x i , x j ) = e x p ( − ∣ ∣ x i − x j ∣ ∣ σ ) k(x_i,x_j)=exp(-\frac{||x_i-x_j||}{\sigma}) k(xi,xj)=exp(−σ∣∣xi−xj∣∣)
Sigmoid Kernel Sigmoid核 k ( x i , x j ) = t a n h ( α x T x j + c ) k(x_i,x_j)=tanh(\alpha x^Tx_j+c) k(xi,xj)=tanh(αxTxj+c) 采用Sigmoid核函数,支持向量机实现的就是一种多层感知器神经网络。
其实还有很多核函数,在参考博客里大家都可以看到这些核函数,对于核函数如何选择的问题,吴恩达教授是这么说的:
如果Feature的数量很大,跟样本数量差不多,这时候选用LR或者是Linear Kernel的SVM
如果Feature的数量比较小,样本数量一般,不算大也不算小,选用SVM+Gaussian Kernel
如果Feature的数量比较小,而样本数量很多,需要手工添加一些feature变成第一种情况
4、软间隔详解
(1)前言
根据之前的介绍,相比于硬间隔,如果样本中与较多的异常点,可能对样本较敏感,不利于模型泛化,于是有了软间隔的支持向量机形式,本文来了解一下此问题。
(2)软间隔最大化
引入松弛变量,使得一部分异常数据也可以满足约束条件: y i ( x i + b ) > = 1 − ε i y_i(x_i+b) >=1 - \varepsilon_i yi(xi+b)>=1−εi,既然约束条件引入了松弛变量,那么点到超平面的距离是不是也要改变,于是调整为: min 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i N ε i s . t . y i ( x i + b ) ≥ 1 − ε i i=1,2...,n ε i ≥ 0 \min \quad \frac{1}{2} ||w||^2+C\sum_{i}^{N}\varepsilon_i \ s.t. \quad y_i(x_i+b) \ge 1 - \varepsilon_i \qquad \text{i=1,2...,n}\ \varepsilon_i \ge 0 min21∣∣w∣∣2+Ci∑Nεi s.t.yi(xi+b)≥1−εii=1,2...,n εi≥0
C:表示惩罚因子,这个值大小表示对误分类数据集的惩罚,调和最大间距和误分类点个数之间的关系。
ε
i
\varepsilon_i
εi:也作为代价。
这也是一个凸二次规划问题,可以求解得到
w
w
w,但b的求解是一个区间范围,让我们来看看是怎么回事,求解流程跟硬间隔没差别,直接得到拉格朗日对偶问题:
max a i > 0 , μ > 0 min w i , b , ε L ( w , b , ε , a , μ ) = 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i N ε i + ∑ i = 1 N a i [ 1 − y i ( w x i + b ) + ε i ] + ∑ i N μ i ε i \max_{a_i>0,\mu>0} \min_{w_i,b,\varepsilon} \quad L(w,b,\varepsilon,a,\mu)= \frac{1}{2} ||w||^2+C\sum_{i}^{N}\varepsilon_i+\sum_{i=1}^{N}a_{i}[1-y_i(wx_i+b)+\varepsilon_i]+\sum_{i}^{N} \mu_i \varepsilon_i ai>0,μ>0maxwi,b,εminL(w,b,ε,a,μ)=21∣∣w∣∣2+Ci∑Nεi+i=1∑Nai[1−yi(wxi+b)+εi]+i∑Nμiεi 继续按照流程走:
对w、b、
ε
\varepsilon
ε 求偏导,让偏导等于0,结果为:
w
=
∑
i
a
i
y
i
x
i
∑
i
a
i
y
i
=
0
C
−
a
i
−
u
i
=
0
w = \sum_{i}a_iy_ix_i \ \sum_{i}a_iy_i = 0 \ C-a_i-u_i =0
w=i∑aiyixi i∑aiyi=0 C−ai−ui=0
代入上面的方程得到:
max
a
i
>
0
,
μ
>
0
L
(
w
,
b
,
ε
,
a
,
μ
)
=
−
1
2
∑
i
∑
j
a
i
a
j
y
i
y
j
(
x
i
∗
x
j
)
+
∑
i
a
i
s
.
t
.
∑
i
N
a
i
y
i
=
0
0
≤
a
i
≤
C
\max_{a_i>0,\mu>0} \quad L(w,b,\varepsilon,a,\mu) = -\frac{1}{2}\sum_{i} \sum_{j}a_{i}a_{j}y_{i}y_{j}(x_i * x_j) + \sum_{i}a_i \ s.t. \quad \sum_{i}^{N}a_iy_i=0 \ \quad 0\le a_i\le C
ai>0,μ>0maxL(w,b,ε,a,μ)=−21i∑j∑aiajyiyj(xi∗xj)+i∑ai s.t.i∑Naiyi=0 0≤ai≤C 去掉符号,将max 转换为 min :
min
a
i
>
0
,
μ
>
0
L
(
w
,
b
,
ε
,
a
,
μ
)
=
1
2
∑
i
∑
j
a
i
a
j
y
i
y
j
(
x
i
∗
x
j
)
−
∑
i
a
i
s
.
t
.
∑
i
N
a
i
y
i
=
0
0
≤
a
i
≤
C
\min_{a_i>0,\mu>0} \quad L(w,b,\varepsilon,a,\mu) = \frac{1}{2}\sum_{i} \sum_{j}a_{i}a_{j}y_{i}y_{j}(x_i * x_j) - \sum_{i}a_i \ s.t. \quad \sum_{i}^{N}a_iy_i=0 \ \quad 0\le a_i\le C
ai>0,μ>0minL(w,b,ε,a,μ)=21i∑j∑aiajyiyj(xi∗xj)−i∑ai s.t.i∑Naiyi=0 0≤ai≤C 这里代入之后就只有一个因子
a
i
a_i
ai,对此方程求解
a
i
a_i
ai
w、b: w = ∑ i a i y i x i w = \sum_{i}a_iy_ix_i \ w=i∑aiyixi b的计算就需要思考了,选取满足 0 ≤ a i ≤ C \quad 0\le a_i\le C 0≤ai≤C的 a i a_i ai,利用这些点来求解b: b = y j − ∑ i a i y i ( x i ∗ x j ) b = y_j-\sum_{i}a_iy_i(x_i*x_j) b=yj−i∑aiyi(xi∗xj) 当然符合这个条件的也不只有一个,存在多个条件。求解平均值作为一个唯一值。
超平面 y = w x + b y = wx+b y=wx+b
和上一篇的硬间隔最大化的线性可分SVM相比,多了一个约束条件: 0 ≤ a i ≤ C 0\le a_i \le C 0≤ai≤C。
5、SMO求解SVM
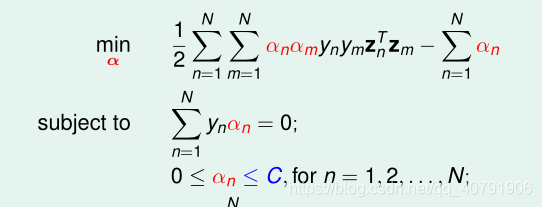
这就是SMO要解决的凸优化问题,它的特殊之处在于:它是另一个问题的对偶问题,还满足KKT条件,怎么充分利用这个特殊性呢?
随机找一个α=(α1,α2,…,αN)。假设它就是最优解,就可以用KKT条件来计算出原问题的最优解(w,b),就是这个样子:
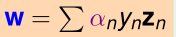
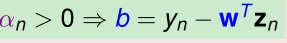
进而可以得到分离超平面:
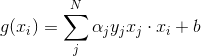
按照SVM的理论,如果这个g(x)是最优的分离超平面,就有:
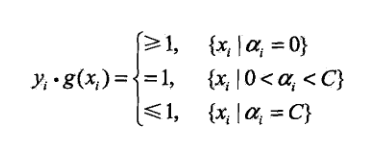
姑且称这个叫g(x)目标条件吧。
根据已有的理论,上面的推导过程是可逆的。也就是说,只要我能找到一个α,它除了满足对偶问题的两个初始限制条件:
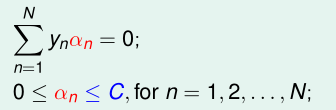
由它求出的分离超平面g(x)还能满足g(x)目标条件,那么这个α就是对偶问题的最优解!!!
至此,我们的思路已经确定了:首先,初始化一个α,让它满足对偶问题的两个初始限制条件,然后不断优化它,使得由它确定的分离超平面满足g(x)目标条件,在优化的过程中始终确保它满足初始限制条件,这样就可以找到最优解。
具体怎么优化α呢?经过思考,我发现必须遵循如下两个基本原则:
每次优化时,必须同时优化α的两个分量,因为只优化一个分量的话,新的α就不再满足初始限制条件中的等式条件了。
每次优化的两个分量应当是违反g(x)目标条件比较多的。就是说,本来应当是大于等于1的,越是小于1违反g(x)目标条件就越多,这样一来,选择优化的两个分量时,就有了基本的标准。
好,我先选择第一个分量吧,α的分量中有等于0的,有等于C的,还有大于0小于C的,直觉告诉我,先从大于0小于C的分量中选择是明智的,如果没有找到可优化的分量时,再从其他两类分量中挑选。
现在,我选了一个分量,就叫它α1吧,这里的1表示它是我选择的第一个要优化的分量,可不是α的第1个分量。
选α2的标准:我为每一个分量算出一个指标E,它是这样的:
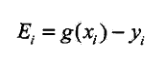
我发现,当|E1-E2|越大时,优化后的α1、α2改变越大。所以,如果E1是正的,那么E2越负越好,如果E1是负的,那么E2越正越好。这样,我就能选到我的α2啦。
怎么优化α1、α2可以确保优化后,它们对应的样本能够满足g(x)目标条件或者违反g(x)目标条件的程度变轻呢?其实只要优化后是在朝着好的方向发展就可以。
再看对偶问题:
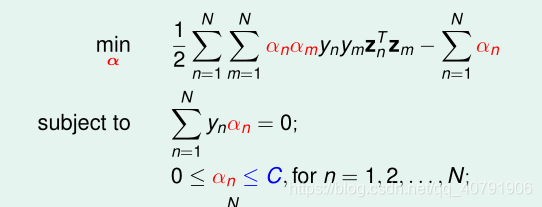
我们发现虽然我不知道怎样优化α1、α2,让它们对应的样本违反g(x)目标条件变轻,但是我们可以让它们优化后目标函数的值变小啊!使目标函数变小,肯定是朝着正确的方向优化!也就肯定是朝着使违反g(x)目标条件变轻的方向优化,二者是一致的。
此时,将α1、α2看做变量,其他分量看做常数,对偶问题就是一个超级简单的二次函数优化问题:
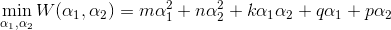
其中:
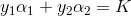
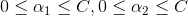
至此,这个问题已经变得非常简单:举例来说明一下,假设y1和y2都等于1,那么第一个限制条件就变成了
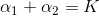
首先,将α1=K-α2代入目标函数,这时目标函数变成了关于α2的一元函数,对α2求导并令导数为0可以求出α2_new。
然后,观察限制条件,第一个条件α1=K-α2相当于
0≦K-α2≦C
进而求得:
K-C≦α2≦K,再加上原有的限制
0≦α2≦C,可得
max(K-C,0)≦α2≦min(K,C)
如果α2_new就在这个限制范围内,OK!求出α1_new,完成一轮迭代。如果α2_new不在这个限制范围内,进行截断,得到新的α2_new_new,据此求得α1_new_new,此轮迭代照样结束。
6、代码实现
(1) 输入数据
这里使用两个原始数据文件 trainingData.txt,testData.txt。
trainingData.txt:
1 -0.214824 0.662756 -1.000000
2 -0.061569 -0.091875 1.000000
3 0.406933 0.648055 -1.000000
4 0.223650 0.130142 1.000000
5 0.231317 0.766906 -1.000000
6 -0.748800 -0.531637 -1.000000
7 -0.557789 0.375797 -1.000000
8 0.207123 -0.019463 1.000000
9 0.286462 0.719470 -1.000000
10 0.195300 -0.179039 1.000000
11 -0.152696 -0.153030 1.000000
12 0.384471 0.653336 -1.000000
13 -0.117280 -0.153217 1.000000
14 -0.238076 0.000583 1.000000
15 -0.413576 0.145681 1.000000
16 0.490767 -0.680029 -1.000000
17 0.199894 -0.199381 1.000000
18 -0.356048 0.537960 -1.000000
19 -0.392868 -0.125261 1.000000
20 0.353588 -0.070617 1.000000
21 0.020984 0.925720 -1.000000
22 -0.475167 -0.346247 -1.000000
23 0.074952 0.042783 1.000000
24 0.394164 -0.058217 1.000000
25 0.663418 0.436525 -1.000000
26 0.402158 0.577744 -1.000000
27 -0.449349 -0.038074 1.000000
28 0.619080 -0.088188 -1.000000
29 0.268066 -0.071621 1.000000
30 -0.015165 0.359326 1.000000
31 0.539368 -0.374972 -1.000000
32 -0.319153 0.629673 -1.000000
33 0.694424 0.641180 -1.000000
34 0.079522 0.193198 1.000000
35 0.253289 -0.285861 1.000000
36 -0.035558 -0.010086 1.000000
37 -0.403483 0.474466 -1.000000
38 -0.034312 0.995685 -1.000000
39 -0.590657 0.438051 -1.000000
40 -0.098871 -0.023953 1.000000
41 -0.250001 0.141621 1.000000
42 -0.012998 0.525985 -1.000000
43 0.153738 0.491531 -1.000000
44 0.388215 -0.656567 -1.000000
45 0.049008 0.013499 1.000000
46 0.068286 0.392741 1.000000
47 0.747800 -0.066630 -1.000000
48 0.004621 -0.042932 1.000000
49 -0.701600 0.190983 -1.000000
50 0.055413 -0.024380 1.000000
51 0.035398 -0.333682 1.000000
52 0.211795 0.024689 1.000000
53 -0.045677 0.172907 1.000000
54 0.595222 0.209570 -1.000000
55 0.229465 0.250409 1.000000
56 -0.089293 0.068198 1.000000
57 0.384300 -0.176570 1.000000
58 0.834912 -0.110321 -1.000000
59 -0.307768 0.503038 -1.000000
60 -0.777063 -0.348066 -1.000000
61 0.017390 0.152441 1.000000
62 -0.293382 -0.139778 1.000000
63 -0.203272 0.286855 1.000000
64 0.957812 -0.152444 -1.000000
65 0.004609 -0.070617 1.000000
66 -0.755431 0.096711 -1.000000
67 -0.526487 0.547282 -1.000000
68 -0.246873 0.833713 -1.000000
69 0.185639 -0.066162 1.000000
70 0.851934 0.456603 -1.000000
71 -0.827912 0.117122 -1.000000
72 0.233512 -0.106274 1.000000
73 0.583671 -0.709033 -1.000000
74 -0.487023 0.625140 -1.000000
75 -0.448939 0.176725 1.000000
76 0.155907 -0.166371 1.000000
77 0.334204 0.381237 -1.000000
78 0.081536 -0.106212 1.000000
79 0.227222 0.527437 -1.000000
80 0.759290 0.330720 -1.000000
81 0.204177 -0.023516 1.000000
82 0.577939 0.403784 -1.000000
83 -0.568534 0.442948 -1.000000
84 -0.011520 0.021165 1.000000
85 0.875720 0.422476 -1.000000
86 0.297885 -0.632874 -1.000000
87 -0.015821 0.031226 1.000000
88 0.541359 -0.205969 -1.000000
89 -0.689946 -0.508674 -1.000000
90 -0.343049 0.841653 -1.000000
91 0.523902 -0.436156 -1.000000
92 0.249281 -0.711840 -1.000000
93 0.193449 0.574598 -1.000000
94 -0.257542 -0.753885 -1.000000
95 -0.021605 0.158080 1.000000
96 0.601559 -0.727041 -1.000000
97 -0.791603 0.095651 -1.000000
98 -0.908298 -0.053376 -1.000000
99 0.122020 0.850966 -1.000000
100 -0.725568 -0.292022 -1.000000
testData.txt:
1 3.542485 1.977398 -1
2 3.018896 2.556416 -1
3 7.551510 -1.580030 1
4 2.114999 -0.004466 -1
5 8.127113 1.274372 1
6 7.108772 -0.986906 1
7 8.610639 2.046708 1
8 2.326297 0.265213 -1
9 3.634009 1.730537 -1
10 0.341367 -0.894998 -1
11 3.125951 0.293251 -1
12 2.123252 -0.783563 -1
13 0.887835 -2.797792 -1
14 7.139979 -2.329896 1
15 1.696414 -1.212496 -1
16 8.117032 0.623493 1
17 8.497162 -0.266649 1
18 4.658191 3.507396 -1
19 8.197181 1.545132 1
20 1.208047 0.213100 -1
21 1.928486 -0.321870 -1
22 2.175808 -0.014527 -1
23 7.886608 0.461755 1
24 3.223038 -0.552392 -1
25 3.628502 2.190585 -1
26 7.407860 -0.121961 1
27 7.286357 0.251077 1
28 2.301095 -0.533988 -1
29 -0.232542 -0.547690 -1
30 3.457096 -0.082216 -1
31 3.023938 -0.057392 -1
32 8.015003 0.885325 1
33 8.991748 0.923154 1
34 7.916831 -1.781735 1
35 7.616862 -0.217958 1
36 2.450939 0.744967 -1
37 7.270337 -2.507834 1
38 1.749721 -0.961902 -1
39 1.803111 -0.176349 -1
40 8.804461 3.044301 1
41 1.231257 -0.568573 -1
42 2.074915 1.410550 -1
43 -0.743036 -1.736103 -1
44 3.536555 3.964960 -1
45 8.410143 0.025606 1
46 7.382988 -0.478764 1
47 6.960661 -0.245353 1
48 8.234460 0.701868 1
49 8.168618 -0.903835 1
50 1.534187 -0.622492 -1
51 9.229518 2.066088 1
52 7.886242 0.191813 1
53 2.893743 -1.643468 -1
54 1.870457 -1.040420 -1
55 5.286862 -2.358286 1
56 6.080573 0.418886 1
57 2.544314 1.714165 -1
58 6.016004 -3.753712 1
59 0.926310 -0.564359 -1
60 0.870296 -0.109952 -1
61 2.369345 1.375695 -1
62 1.363782 -0.254082 -1
63 7.279460 -0.189572 1
64 1.896005 0.515080 -1
65 8.102154 -0.603875 1
66 2.529893 0.662657 -1
67 1.963874 -0.365233 -1
68 8.132048 0.785914 1
69 8.245938 0.372366 1
70 6.543888 0.433164 1
71 -0.236713 -5.766721 -1
72 8.112593 0.295839 1
73 9.803425 1.495167 1
74 1.497407 -0.552916 -1
75 1.336267 -1.632889 -1
76 9.205805 -0.586480 1
77 1.966279 -1.840439 -1
78 8.398012 1.584918 1
79 7.239953 -1.764292 1
80 7.556201 0.241185 1
81 9.015509 0.345019 1
82 8.266085 -0.230977 1
83 8.545620 2.788799 1
84 9.295969 1.346332 1
85 2.404234 0.570278 -1
86 2.037772 0.021919 -1
87 1.727631 -0.453143 -1
88 1.979395 -0.050773 -1
89 8.092288 -1.372433 1
90 1.667645 0.239204 -1
91 9.854303 1.365116 1
92 7.921057 -1.327587 1
93 8.500757 1.492372 1
94 1.339746 -0.291183 -1
95 3.107511 0.758367 -1
96 2.609525 0.902979 -1
97 3.263585 1.367898 -1
98 2.912122 -0.202359 -1
99 1.731786 0.589096 -1
100 2.387003 1.573131 -1
(2)SMO算法实现
定义数据结构体optStruct,用于缓存,提高运行速度。SMO算法具体实现如下
"""
支持向量机代码实现
SMO(Sequential Minimal Optimization)最小序列优化
"""
import numpy as np
#核转换函数(一个特征空间映射到另一个特征空间,低维空间映射到高维空间)
#高维空间解决线性问题,低维空间解决非线性问题
#线性内核 = 原始数据矩阵(100*2)与原始数据第一行矩阵转秩乘积(2*1) =>(100*1)
#非线性内核公式:k(x,y) = exp(-||x - y||**2/2*(e**2))
#1.原始数据每一行与原始数据第一行作差,
#2.平方
def kernelTrans(dataMat, rowDataMat, kTup):
m,n=np.shape(dataMat)
#初始化核矩阵 m*1
K = np.mat(np.zeros((m,1)))
if kTup[0] == 'lin': #线性核
K = dataMat*rowDataMat.T
elif kTup[0] == 'rbf':#非线性核
for j in range(m):
#xi - xj
deltaRow = dataMat[j,:] - rowDataMat
K[j] = deltaRow*deltaRow.T
#1*m m*1 => 1*1
K = np.exp(K/(-2*kTup[1]**2))
else: raise NameError('Houston We Have a Problem -- That Kernel is not recognized')
return K
#定义数据结构体,用于缓存,提高运行速度
class optStruct:
def __init__(self, dataSet, labelSet, C, toler, kTup):
self.dataMat = np.mat(dataSet) #原始数据,转换成m*n矩阵
self.labelMat = np.mat(labelSet).T #标签数据 m*1矩阵
self.C = C #惩罚参数,C越大,容忍噪声度小,需要优化;反之,容忍噪声度高,不需要优化;
#所有的拉格朗日乘子都被限制在了以C为边长的矩形里
self.toler = toler #容忍度
self.m = np.shape(self.dataMat)[0] #原始数据行长度
self.alphas = np.mat(np.zeros((self.m,1))) # alpha系数,m*1矩阵
self.b = 0 #偏置
self.eCache = np.mat(np.zeros((self.m,2))) # 保存原始数据每行的预测值
self.K = np.mat(np.zeros((self.m,self.m))) # 核转换矩阵 m*m
for i in range(self.m):
self.K[:,i] = kernelTrans(self.dataMat, self.dataMat[i,:], kTup)
#计算原始数据第k项对应的预测误差 1*m m*1 =>1*1
#oS:结构数据
#k: 原始数据行索引
def calEk(oS, k):
#f(x) = w*x + b
fXk = float(np.multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)
Ek = fXk - float(oS.labelMat[k])
return Ek
#在alpha有改变都要更新缓存
def updateEk(oS, k):
Ek = calEk(oS, k)
oS.eCache[k] = [1, Ek]
#第一次通过selectJrand()随机选取j,之后选取与i对应预测误差最大的j(步长最大)
def selectJ(i, oS, Ei):
#初始化
maxK = -1 #误差最大时对应索引
maxDeltaE = 0 #最大误差
Ej = 0 # j索引对应预测误差
#保存每一行的预测误差值 1相对于初始化为0的更改
oS.eCache[i] = [1,Ei]
#获取数据缓存结构中非0的索引列表(先将矩阵第0列转化为数组)
validEcacheList = np.nonzero(oS.eCache[:,0].A)[0]
#遍历索引列表,寻找最大误差对应索引
if len(validEcacheList) > 1:
for k in validEcacheList:
if k == i:
continue
Ek = calEk(oS, k)
deltaE = abs(Ei - Ek)
if(deltaE > maxDeltaE):
maxK = k
maxDeltaE = deltaE
Ej = Ek
return maxK, Ej
else:
#随机选取一个不等于i的j
j = selectJrand(i, oS.m)
Ej = calEk(oS, j)
return j,Ej
#随机选取一个不等于i的索引
def selectJrand(i, m):
j = i
while (j == i):
j = int(np.random.uniform(0, m))
return j
#alpha范围剪辑
def clipAlpha(aj, L, H):
if aj > H:
aj = H
if aj < L:
aj = L
return aj
#从文件获取特征数据,标签数据
def loadDataSet(fileName):
dataSet = []; labelSet = []
fr = open(fileName)
for line in fr.readlines():
#分割
lineArr = line.strip().split('\t')
dataSet.append([float(lineArr[0]), float(lineArr[1])])
labelSet.append(float(lineArr[2]))
return dataSet, labelSet
#计算 w 权重系数
def calWs(alphas, dataSet, labelSet):
dataMat = np.mat(dataSet)
#1*100 => 100*1
labelMat = np.mat(labelSet).T
m, n = np.shape(dataMat)
w = np.zeros((n, 1))
for i in range(m):
w += np.multiply(alphas[i]*labelMat[i], dataMat[i,:].T)
return w
#计算原始数据每一行alpha,b,保存到数据结构中,有变化及时更新
def innerL(i, oS):
#计算预测误差
Ei = calEk(oS, i)
#选择第一个alpha,违背KKT条件2
#正间隔,负间隔
if ((oS.labelMat[i] * Ei < -oS.toler) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i] * Ei > oS.toler) and (oS.alphas[i] > 0)):
#第一次随机选取不等于i的数据项,其后根据误差最大选取数据项
j, Ej = selectJ(i, oS, Ei)
#初始化,开辟新的内存
alphaIold = oS.alphas[i].copy()
alphaJold = oS.alphas[j].copy()
#通过 a1y1 + a2y2 = 常量
# 0 <= a1,a2 <= C 求出L,H
if oS.labelMat[i] != oS.labelMat[j]:
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
if L == H :
print ("L == H")
return 0
#内核分母 K11 + K22 - 2K12
eta = oS.K[i, i] + oS.K[j, j] - 2.0*oS.K[i, j]
if eta <= 0:
print ("eta <= 0")
return 0
#计算第一个alpha j
oS.alphas[j] += oS.labelMat[j]*(Ei - Ej)/eta
#修正alpha j的范围
oS.alphas[j] = clipAlpha(oS.alphas[j], L, H)
#alpha有改变,就需要更新缓存数据
updateEk(oS, j)
#如果优化后的alpha 与之前的alpha变化很小,则舍弃,并重新选择数据项的alpha
if (abs(oS.alphas[j] - alphaJold) < 0.00001):
print ("j not moving enough, abandon it.")
return 0
#计算alpha对的另一个alpha i
# ai_new*yi + aj_new*yj = 常量
# ai_old*yi + ai_old*yj = 常量
# 作差=> ai = ai_old + yi*yj*(aj_old - aj_new)
oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])
#alpha有改变,就需要更新缓存数据
updateEk(oS, i)
#计算b1,b2
# y(x) = w*x + b => b = y(x) - w*x
# w = aiyixi(i= 1->N求和)
#b1_new = y1_new - (a1_new*y1*k11 + a2_new*y2*k21 + ai*yi*ki1(i = 3 ->N求和 常量))
#b1_old = y1_old - (a1_old*y1*k11 + a2_old*y2*k21 + ai*yi*ki1(i = 3 ->N求和 常量))
#作差=> b1_new = b1_old + (y1_new - y1_old) - y1*k11*(a1_new - a1_old) - y2*k21*(a2_new - a2_old)
# => b1_new = b1_old + Ei - yi*(ai_new - ai_old)*kii - yj*(aj_new - aj_old)*kij
#同样可推得 b2_new = b2_old + Ej - yi*(ai_new - ai_old)*kij - yj*(aj_new - aj_old)*kjj
bi = oS.b - Ei - oS.labelMat[i]*(oS.alphas[i] - alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j] - alphaJold)*oS.K[i,j]
bj = oS.b - Ej - oS.labelMat[i]*(oS.alphas[i] - alphaIold)*oS.K[i,j] - oS.labelMat[j]*(oS.alphas[j] - alphaJold)*oS.K[j,j]
#首选alpha i,相对alpha j 更准确
if (0 < oS.alphas[i]) and (oS.alphas[i] < oS.C):
oS.b = bi
elif (0 < oS.alphas[j]) and (oS.alphas[j] < oS.C):
oS.b = bj
else:
oS.b = (bi + bj)/2.0
return 1
else:
return 0
#完整SMO核心算法,包含线性核核非线性核,返回alpha,b
#dataSet 原始特征数据
#labelSet 标签数据
#C 凸二次规划参数
#toler 容忍度
#maxInter 循环次数
#kTup 指定核方式
#程序逻辑:
#第一次全部遍历,遍历后根据alpha对是否有修改判断,
#如果alpha对没有修改,外循环终止;如果alpha对有修改,则继续遍历属于支持向量的数据。
#直至外循环次数达到maxIter
#相比简单SMO算法,运行速度更快,原因是:
#1.不是每一次都全量遍历原始数据,第一次遍历原始数据,
#如果alpha有优化,就遍历支持向量数据,直至alpha没有优化,然后再转全量遍历,这是如果alpha没有优化,循环结束;
#2.外循环不需要达到maxInter次数就终止;
def smoP(dataSet, labelSet, C, toler, maxInter, kTup = ('lin', 0)):
#初始化结构体类,获取实例
oS = optStruct(dataSet, labelSet, C, toler, kTup)
iter = 0
#全量遍历标志
entireSet = True
#alpha对是否优化标志
alphaPairsChanged = 0
#外循环 终止条件:1.达到最大次数 或者 2.alpha对没有优化
while (iter < maxInter) and ((alphaPairsChanged > 0) or (entireSet)):
alphaPairsChanged = 0
#全量遍历 ,遍历每一行数据 alpha对有修改,alphaPairsChanged累加
if entireSet:
for i in range(oS.m):
alphaPairsChanged += innerL(i, oS)
print ("fullSet, iter: %d i:%d, pairs changed %d" %(iter, i, alphaPairsChanged))
iter += 1
else:
#获取(0,C)范围内数据索引列表,也就是只遍历属于支持向量的数据
nonBounds = np.nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
for i in nonBounds:
alphaPairsChanged += innerL(i, oS)
print ("non-bound, iter: %d i:%d, pairs changed %d" %(iter, i, alphaPairsChanged))
iter += 1
#全量遍历->支持向量遍历
if entireSet:
entireSet = False
#支持向量遍历->全量遍历
elif alphaPairsChanged == 0:
entireSet = True
print ("iteation number: %d"% iter)
print ("entireSet :%s"% entireSet)
print ("alphaPairsChanged :%d"% alphaPairsChanged)
return oS.b,oS.alphas
#绘制支持向量
def drawDataMap(dataArr,labelArr,b,alphas):
import matplotlib.pyplot as plt
#alphas.A>0 获取大于0的索引列表,只有>0的alpha才对分类起作用
svInd=np.nonzero(alphas.A>0)[0]
#分类数据点
classified_pts = {'+1':[],'-1':[]}
for point,label in zip(dataArr,labelArr):
if label == 1.0:
classified_pts['+1'].append(point)
else:
classified_pts['-1'].append(point)
fig = plt.figure()
ax = fig.add_subplot(111)
#绘制数据点
for label,pts in classified_pts.items():
pts = np.array(pts)
ax.scatter(pts[:, 0], pts[:, 1], label = label)
#绘制分割线
w = calWs(alphas, dataArr, labelArr)
#函数形式:max( x ,key=lambda a : b ) # x可以是任何数值,可以有多个x值
#先把x值带入lambda函数转换成b值,然后再将b值进行比较
x1, _=max(dataArr, key=lambda x:x[0])
x2, _=min(dataArr, key=lambda x:x[0])
a1, a2 = w
y1, y2 = (-b - a1*x1)/a2, (-b - a1*x2)/a2
#矩阵转化为数组.A
ax.plot([x1, x2],[y1.A[0][0], y2.A[0][0]])
#绘制支持向量
for i in svInd:
x, y= dataArr[i]
ax.scatter([x], [y], s=150, c ='none', alpha=0.7, linewidth=1.5, edgecolor = '#AB3319')
plt.show()
#alpha>0对应的数据才是支持向量,过滤不是支持向量的数据
sVs= np.mat(dataArr)[svInd] #get matrix of only support vectors
print ("there are %d Support Vectors.\n" % np.shape(sVs)[0])
#训练结果
def getTrainingDataResult(dataSet, labelSet, b, alphas, k1=1.3):
datMat = np.mat(dataSet)
#100*1
labelMat = np.mat(labelSet).T
#alphas.A>0 获取大于0的索引列表,只有>0的alpha才对分类起作用
svInd=np.nonzero(alphas.A>0)[0]
sVs=datMat[svInd]
labelSV = labelMat[svInd];
m,n = np.shape(datMat)
errorCount = 0
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
# y(x) = w*x + b => b = y(x) - w*x
# w = aiyixi(i= 1->N求和)
predict = kernelEval.T * np.multiply(labelSV, alphas[svInd]) + b
if np.sign(predict)!=np.sign(labelSet[i]): errorCount += 1
print ("the training error rate is: %f" % (float(errorCount)/m))
def getTestDataResult(dataSet, labelSet, b, alphas, k1=1.3):
datMat = np.mat(dataSet)
#100*1
labelMat = np.mat(labelSet).T
#alphas.A>0 获取大于0的索引列表,只有>0的alpha才对分类起作用
svInd=np.nonzero(alphas.A>0)[0]
sVs=datMat[svInd]
labelSV = labelMat[svInd];
m,n = np.shape(datMat)
errorCount = 0
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
# y(x) = w*x + b => b = y(x) - w*x
# w = aiyixi(i= 1->N求和)
predict=kernelEval.T * np.multiply(labelSV,alphas[svInd]) + b
if np.sign(predict)!=np.sign(labelSet[i]): errorCount += 1
print ("the test error rate is: %f" % (float(errorCount)/m))
(3)测试代码
"""
测试代码
"""
#通过训练数据计算 b, alphas
dataArr,labelArr = loadDataSet('./trainingData.txt')
b, alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', 0.10))
drawDataMap(dataArr,labelArr,b,alphas)
getTrainingDataResult(dataArr, labelArr, b, alphas, 0.10)
dataArr1,labelArr1 = loadDataSet('./testData.txt')
#测试结果
getTestDataResult(dataArr1, labelArr1, b, alphas, 0.10)
通过训练数据计算出 b, 权重矩阵,从而分类超平面和决策分类函数就明确了,然后测试数据以决策分类函数进行预测。
这里采用高斯核RBF。
(4)运行结果

“j not moving enough, abandon it” 表示数据项对应的 和 非常接近,不需要优化;
“fullSet” 表示全量数据遍历;
“non-bound” 表示非边界遍历,也就是只遍历属于支持向量的数据项。
支持向量的数据项绘制结果:
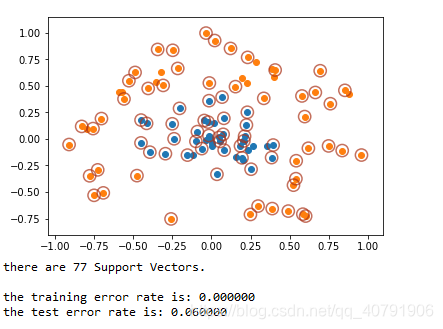
可以看出,有77个支持向量,训练差错率是0,测试差错率6%。




 本文深入解析支持向量机(SVM)的基本原理,包括硬间隔与软间隔的概念,核函数的应用,以及SMO算法的实现细节。通过实例演示SVM如何处理线性和非线性分类问题,同时介绍了SMO算法在SVM中的应用,实现高效的模型训练。
本文深入解析支持向量机(SVM)的基本原理,包括硬间隔与软间隔的概念,核函数的应用,以及SMO算法的实现细节。通过实例演示SVM如何处理线性和非线性分类问题,同时介绍了SMO算法在SVM中的应用,实现高效的模型训练。
















 1123
1123

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








