并查集——徒子徒孙

多个黑帮混战，但是由于都光着膀子，并且每个人只认识自己的师父（每个黑帮祖师爷只认识自己，毕竟目中无人嘛！）。现在有两个人碰在一起，但是他们不知道对方是敌人还是一个帮派的，请你来告诉他们（祖师爷一样就代表是同一个黑帮）

样例输入：

n，m               n代表一共n个人，m代表一共m个师徒关系

接下来m行，每行两个整数，第一个整数代表徒弟的编号，第二个代表他的师父

接下来输入x，y请判断x和y是不是同一个黑帮的呢

样例输出：

yes  or   no

 

解题代码：

#include<iostream>
using namespace std;
int n,m,x,y;
int par[10000];//此数组对应每个人所对应的师父 
int find(int a){
	if (par[a] == a){
	    return a;
    }else{
		return par[a] = find(par[a]);
	}
}
int main()
{
	for(int i=0;i<10000;i++){
		par[i]=i;//数组初始化，先使每个人把自己做为师父 
	}
	cin>>n>>m;
	for(int i=0;i<m;i++){
		int x1,y1;
		cin>>x1>>y1;
		par[x1]=y1; //更新师徒关系 
	} 
	cin>>x>>y;
	x=find(x);
	y=find(y);
	if(x==y)cout<<"yes"<<endl;
	else cout<<"no"<<endl;
	return 0;
} 

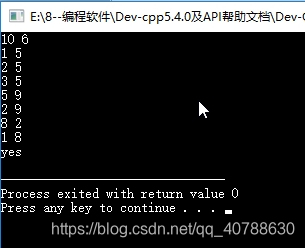
运行结果：