C程序-ACM竞赛-Zrain的文学题

Description

当你我遇见，每个名字每张笑脸。我们相聚在这里，但终将要离开。在长亭下许下的誓言，在柳树旁见过的花瓣飘飞。我们在旖旎烂熳的夕阳下，约定好一定会再相见。

当你我再见，万水千山已走遍。等风过老树叶尖，把故事连缀成篇。当笙箫响起时，相片在心底浮现；当离歌唱尽后，只剩梧桐树枯萎的叶片。

不禁唱起了那首美好的歌“开始的开始，我们都是孩子。最后的最后，渴望变成天使。歌谣的歌谣，藏着童话的影子。孩子的孩子…该要飞往哪儿去。”

ZRain不知道收到了什么刺激，开始迷恋上了诗歌和音乐（虽然他的五音和文采真的…）

现在ZRain要让n个孩子变成天使，每个孩子都有一个RP值，当RP值为一个质数时孩子就能变成天使。但是改变孩子的RP值是有代价的，比如rp从x改到y需要付出|x-y|的代价。ZRain真的太喜欢这些孩子了，他希望这些孩子都变成可爱的天使，但又希望付出最小的代价。 

Input

第一行为一个正整数n，表示孩子的个数(n <= 10^5)。

后面有n行，每行一个正整数rp，表示孩子初始的rp值(rp< = 10^7)。

Output

一共有n行，第i行的整数表示ZRain让第i个孩子变成天使所要付出的最小代价。

Sample Input

5
5
18
22
30
92

Sample Output

0
1
1
1
3

HINT

样例解释：

可以将每个孩子的rp值分别改成5,17,23,29,89。

思路：根据题目先求出100W以内的素数，然后在直接查找rp所在区间，直接一个一个比较查找会超时（时间复杂度为n），因此必须用时间复杂度小的查找方法，二分法的时间复杂度为（），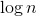

代码：

#include <iostream>
#include <stdio.h>
#include <stdlib.h>

const int N = 10000001;
bool PRIME[N]={0};//素数表
int PrimeTable[664579 + 10];//这里的664579是1  - 10000000里面的素数的最大个数

void getPrimetable()//求素数 
{
    for(int i=3;i<=3333;i+=2)
    {
        if (PRIME[i]==0)
        {
            for(int j=i*i;j<N;j+=2*i)//检查9,15（3*5），21（3*7）。。。。奇数乘以偶数得到一偶数，所以这里j+=2*i
            {
                PRIME[j]=1;//不和要求，不是素数
            }
        }
    }

    int total_prime=1;//考虑2是素数
    PrimeTable[1]=2;
    for (int i=3;i<N;i++)
    {
        if (i%2 != 0 && PRIME[i]==0)//这里排除掉所有的偶数
        {
            PrimeTable[++total_prime]=i;
        }
    }

}


int binsearch(int *sortedSeq, int seqLength, int keyData)//二分法查找 
{
    int low = 0, mid, high = seqLength - 1;

    while (low <= high)
    {
        mid = (low + high) / 2;//奇数，无论奇偶，有个值就行
        if (keyData < sortedSeq[mid])
        {
            high = mid - 1;//是mid-1，因为mid已经比较过了
        }
        else if (keyData > sortedSeq[mid])
        {
            low = mid + 1;
        }
        else
        {
            return mid;
        }
    }
    return mid;
}

int main( ) 
{
    int i,j,n,rp,a,b,c;
    getPrimetable();
    scanf("%d",&n);
    for(j=0;j<n;j++)
    {
        scanf("%d",&rp);
        c=binsearch(PrimeTable,664579,rp);//得到一个下标 
        
        //确定RP值所在区间 
        a=rp-PrimeTable[c];
        if(a>=0)
        {
            b=PrimeTable[c+1]-rp;//返回下标值在rp右边，比rp大 
        }
        else
        {
            b=rp-PrimeTable[c-1];//返回下标值在rp左边，比rp小 
            a=-a;
        }
        if(a>b)//输出与rp最近的素数的差值 
        printf("%d\n",b);
        else
        printf("%d\n",a);
    }


    return 0;
}