tensorflow所构建的体系是清楚明了的,所以我们只需要在其提供的默认图上添加各种op,然后执行相应的op即可
下面的这个例子将从拟合一维函数的角度对tensorflow编程进行一个简单的介绍
1.编程思路
在区间[-5, 5]内随机生成若干个点,作为函数的自变量采样点序列x,然后手动生成这个自变量序列所对应的函数值序列y,这个序列要加上噪声。
# 首先生成x坐标数据
x = np.float32(np.random.rand(1, num_of_x)*10-5)
x = np.sort(x)
# 然后生成y坐标数据,注意产生噪声
y = np.sin(x) + np.random.normal(size=x.shape)*0.5然后我们使用单隐藏层全连接网络(因为神经网络的 万能近似定理 告诉我们,单隐藏层就足够了,差别在于神经元的个数,和隐藏层的层数关系不大),设置神经元个数为200,输入一维,输出也是一维,如下图:

输入 x_data 是一个数据点,维度 1*1,令隐藏层的 w 矩阵为 1*200,b 为 1*200,那么将得到 out1 = x*w+b 维度 1*200,接下来让out1通过输出层,输出层 w 矩阵为200*1,b 为 1*1,那么将得到 out2 = out1 * w + b,最后结果仍然是一个数
# 设置全链接网络层
# w每一层,第一个维度是输入维度,第二个维度是本层神经元个数
w = [tf.Variable(tf.random_normal([1, 200])), tf.Variable(tf.random_normal([200, 1]))]
b = [tf.Variable(tf.random_normal([1, 200])), tf.Variable(tf.random_normal([1, 1]))]
x_data = tf.placeholder(tf.float32)
y_data = tf.placeholder(tf.float32)
out = []
out.append(tf.sigmoid(x_data * w[0] + b[0]))
#out.append(x_data * w[0] + b[0])
out.append(tf.matmul(out[0], w[1]) + b[1])
y_predict = tf.reduce_mean(out[1])使用平方误差函数作为损失函数(或者说,评估函数),设置一个节点对loss进行最小化操作。
# 设置误差函数
loss = tf.reduce_mean(tf.square(y_predict - y_data))
# 设置优化操作
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
rzc_train = optimizer.minimize(loss)输入的x_data和y_data都是一次训练只输入一个点,所以需要设置成placeholder占位符,每次运行“loss最小化操作”这个节点时都喂入相应的数据即可:
x_data = tf.placeholder(tf.float32)
y_data = tf.placeholder(tf.float32)
...
sess.run(rzc_train, feed_dict={x_data:x[0][i%num_of_x], y_data:y[0][i%num_of_x]})2.编程中遇到的问题
1. 注意运行图中的某一个节点时,一定要注意该节点值的计算过程中是否用到了其他占位符,如果用到了,那就必须提供这些占位符的具体值,否则将会报错。如果填入其他值,还可以实现某些技巧性的效果,如下:
# 希望根据已经计算好的w、b矩阵得到网络所代表的函数的函数图像
# 这里的x=array([[-9.74, ...]]),是一个array矩阵,x[0]才是这个矩阵的第一行
y_draw = [sess.run(y_predict, feed_dict={x_data:i}) for i in x[0]]2. 学习率设置的过高(有时0.01都算过高),将会导致梯度下降学习算法发散失效。反正设置得小一点总是没有任何问题的,
3.结果
如果不引入神经元激活函数(本程序中是sigmoid),那么这个网络的输出将是输入的纯线性函数,也就是说,只能拟合最佳直线,如图:
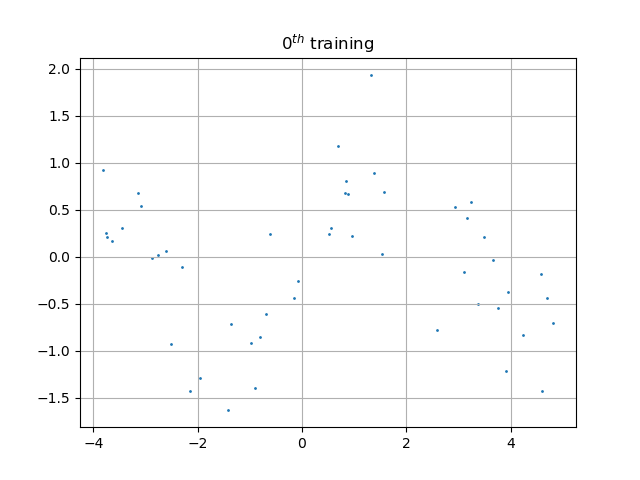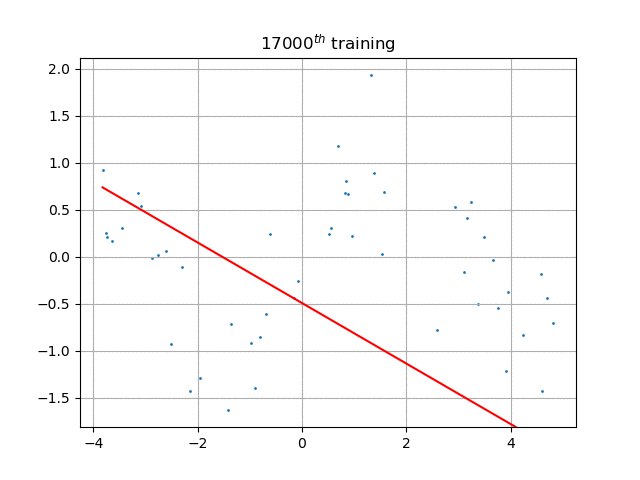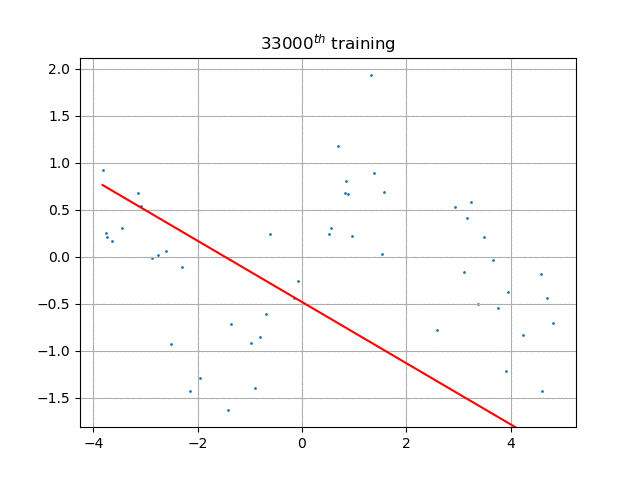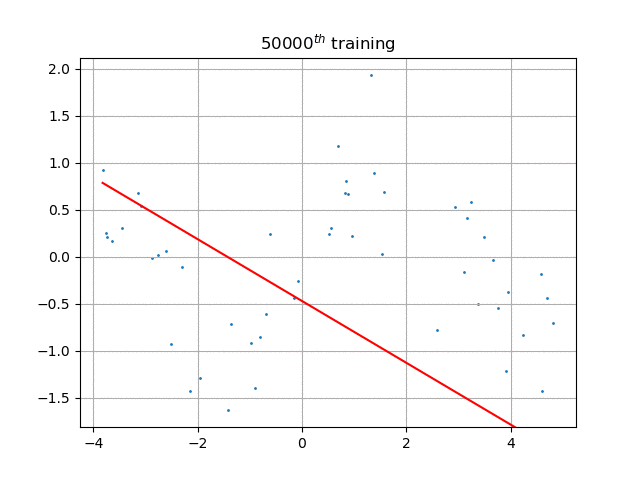
如果引入激活函数,将按照正常方式工作:
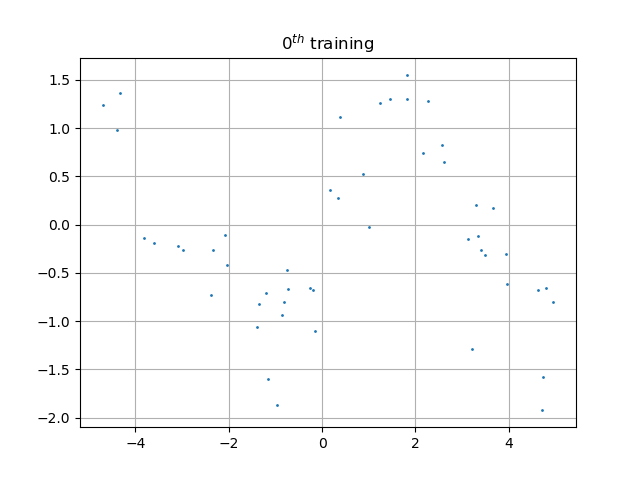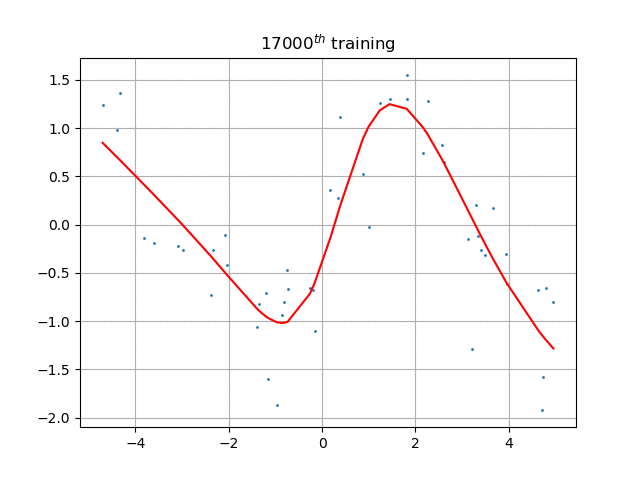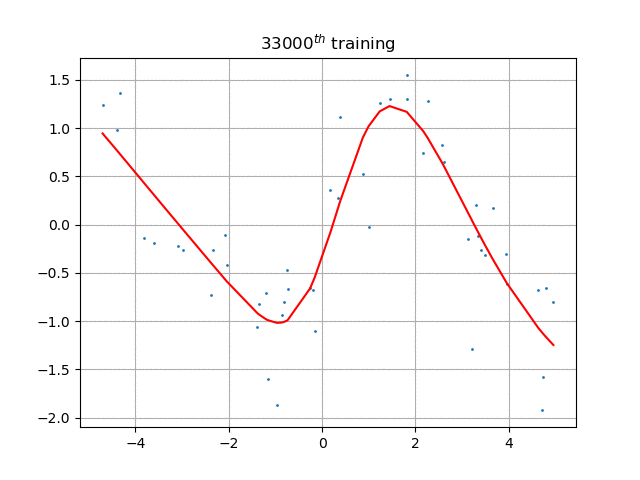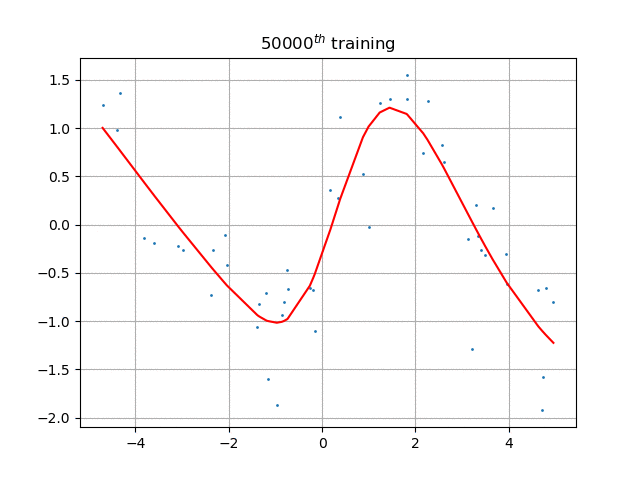
























 7万+
7万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








