If the degree of the numerator of a rational function is one greater than the degree of the denominator, the graph has an oblique(slanted)asymptote. We find an equation for the asymptote by dividing numerator by denominator to express f as a linear function plus a remainder that goes to zero as  . Here is an example.
. Here is an example.

The function f(x) = x is called the identity function.
All composites of continuous functions are continuous.
The rules of exponents tell us that ![]() if a is any number different from zero. They also tell us that
if a is any number different from zero. They also tell us that ![]() if n is any positive number.
if n is any positive number.
![]() .
.
max { a, b } = (a+b)/2 + |a+b|/2
min { a, b } = (a+b)/2 - |a+b|/2
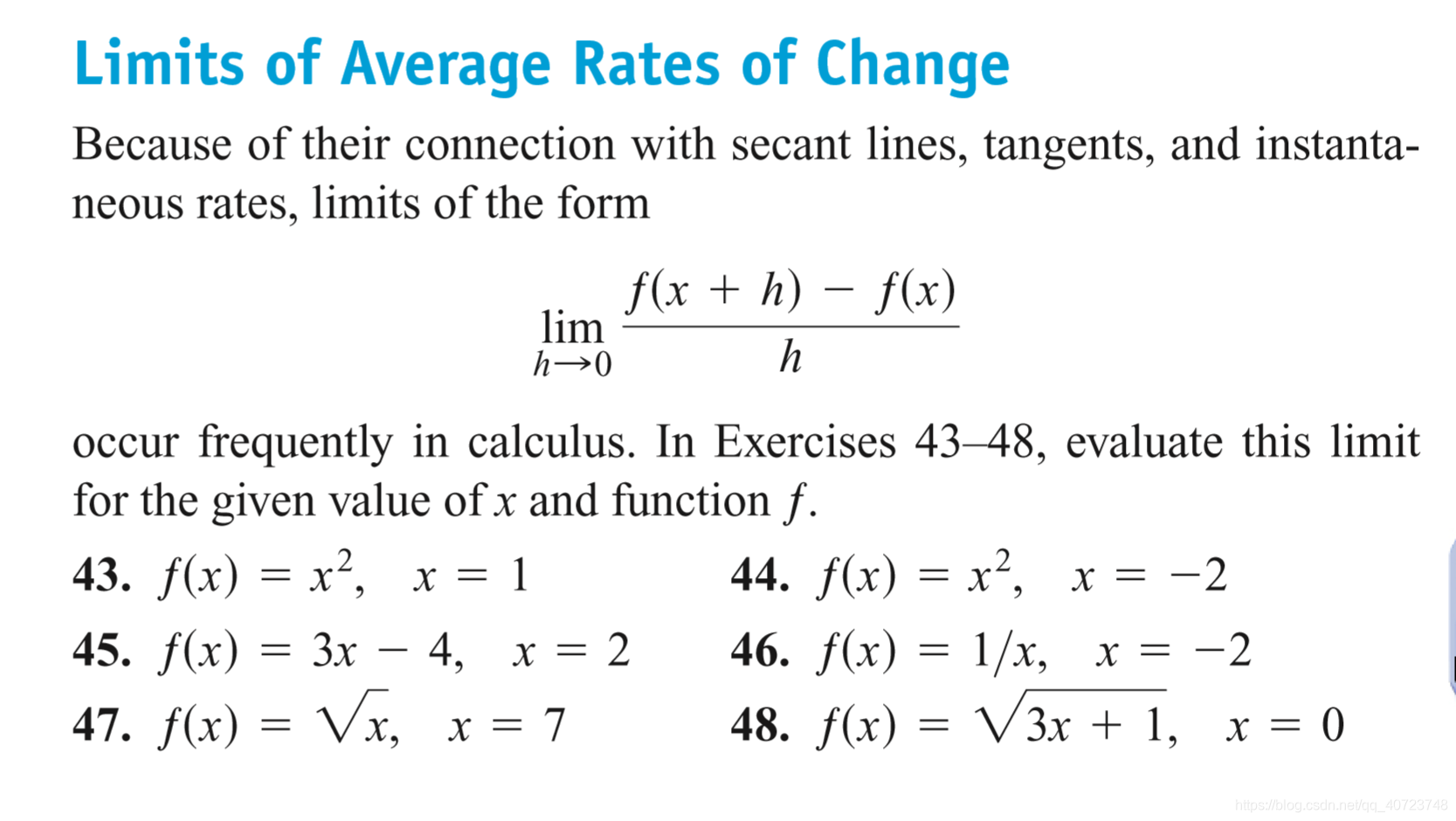
Answer:
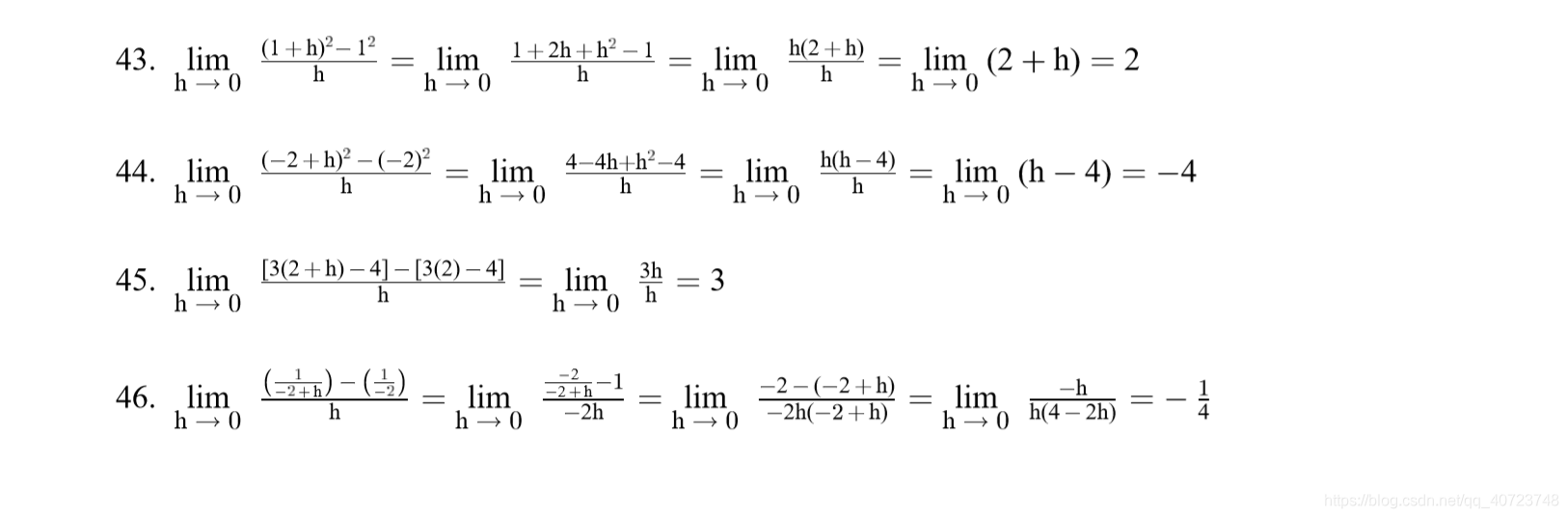
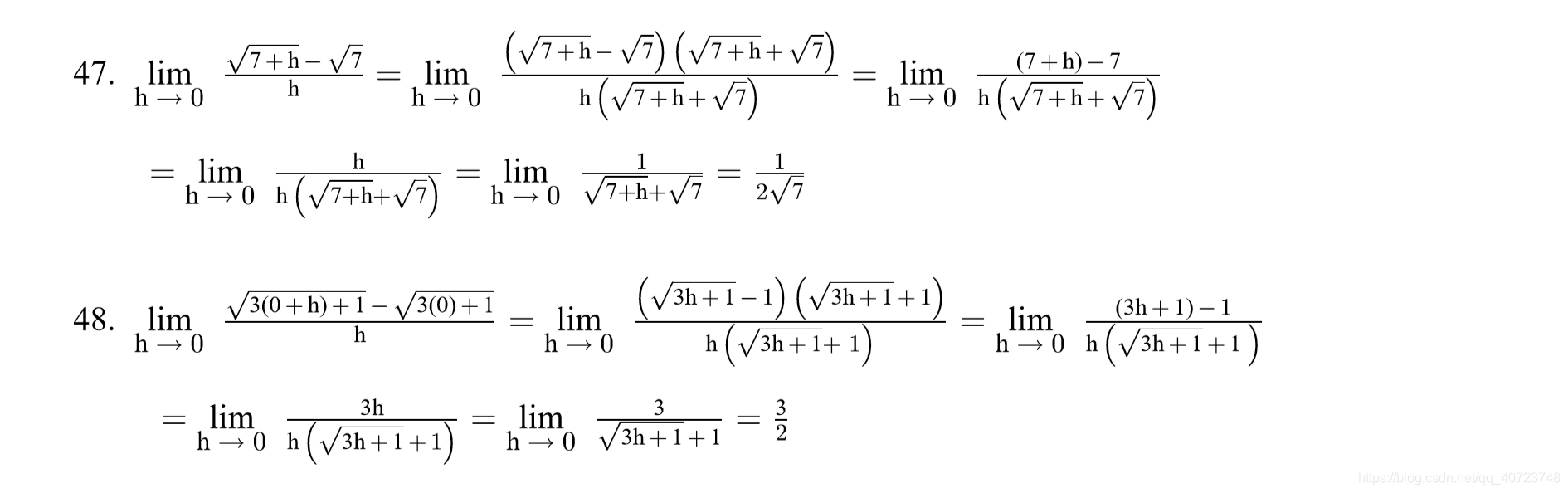
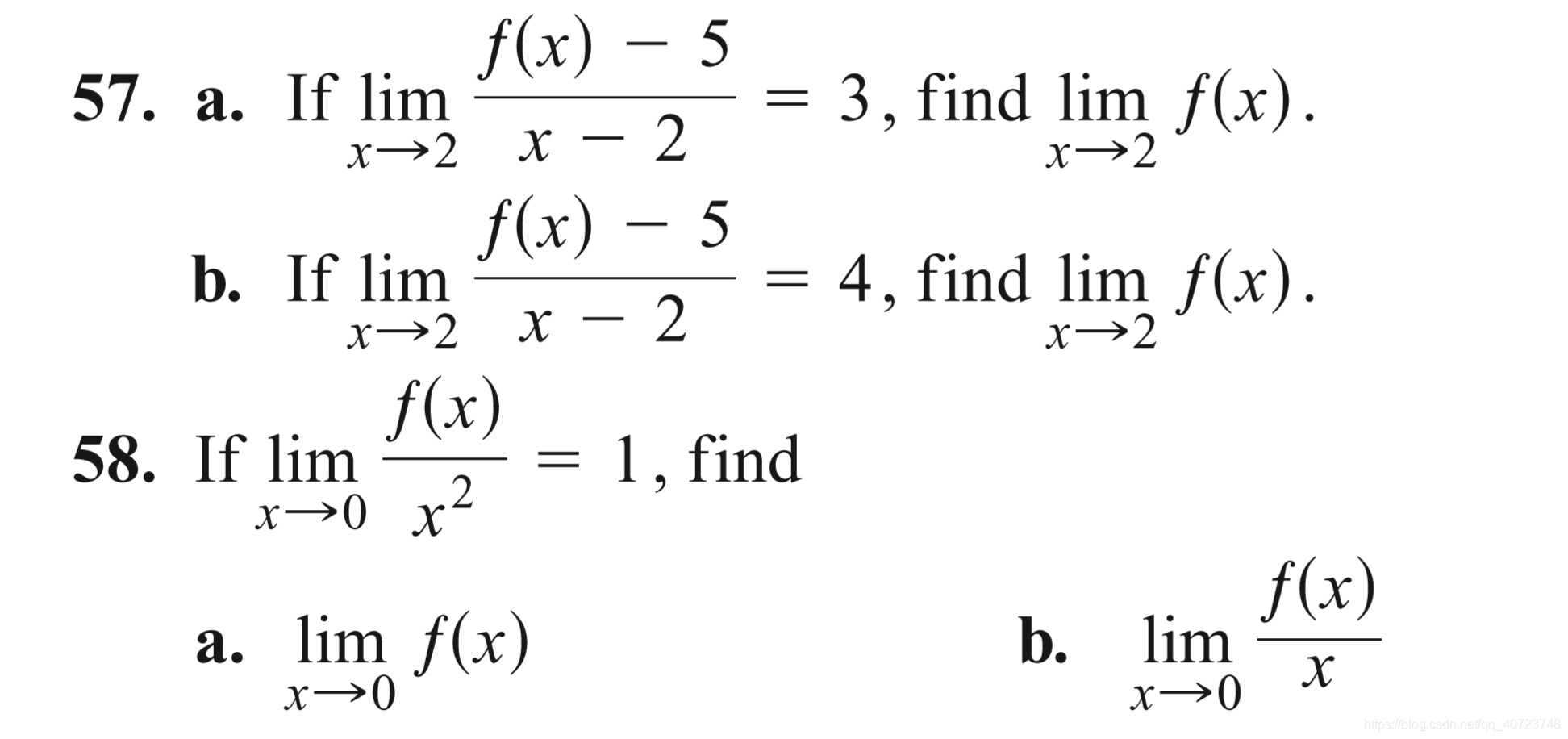
Answer:
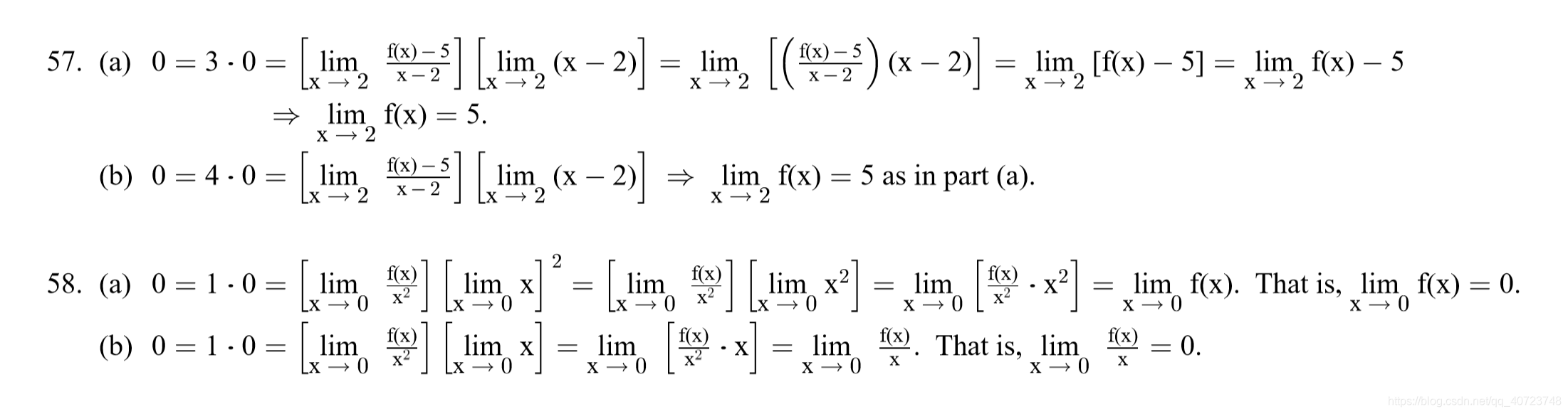

Answer:
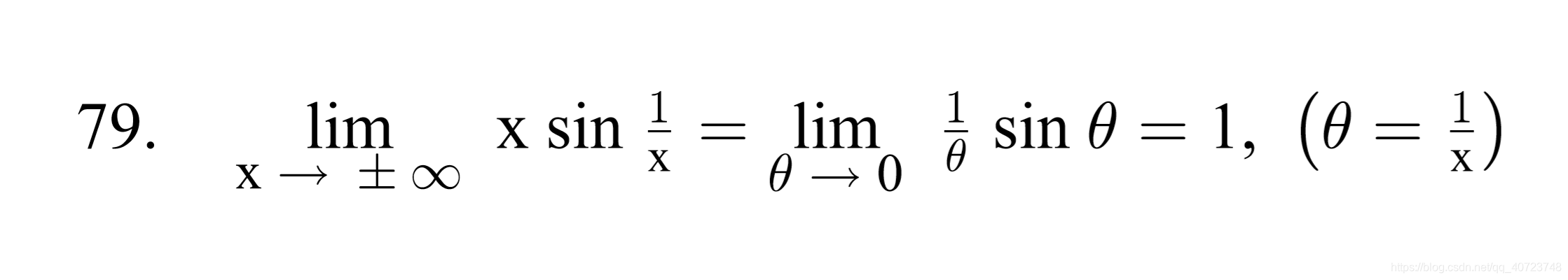
At what points are the following functions continuous?
1. ![]()
2. ![]() 3.
3. ![]()
Answer:
-
 (k is any integer)
(k is any integer) -

-

Lorentz contraction
In relativity theory, the length of an object, say a rocket, appears to an observer to depend on the speed at which the object is traveling with respect to the observer. If the observer measures the rocket's length as at rest, then at speed
 the length will appear to be
the length will appear to be .
.This equation is the Lorentz contraction formula. Here, c is the speed of light in a vacuum.
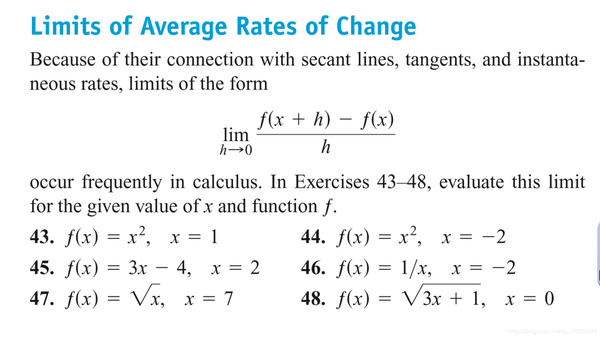
Answer:
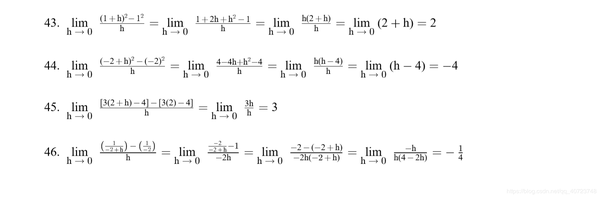
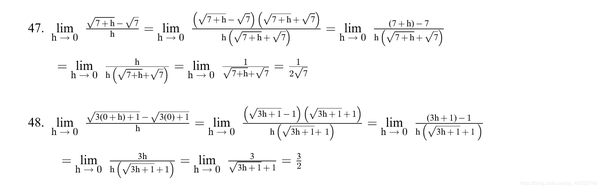
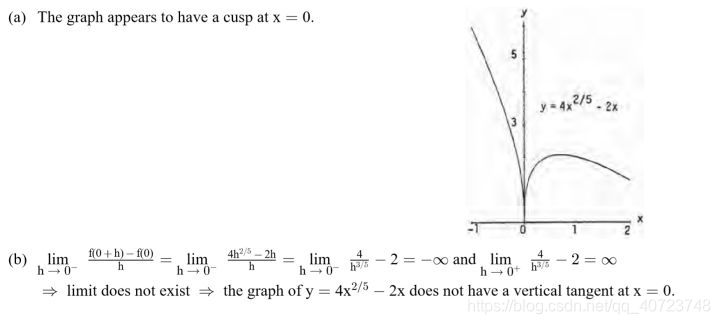
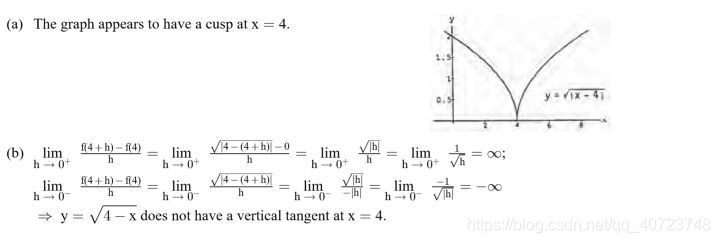
Graph the following curves, where do the graph appear to have vertical tangents? Confirm your findings with limit calculations.
![]()
![]()
![]()
![]()
![]()
Answer:

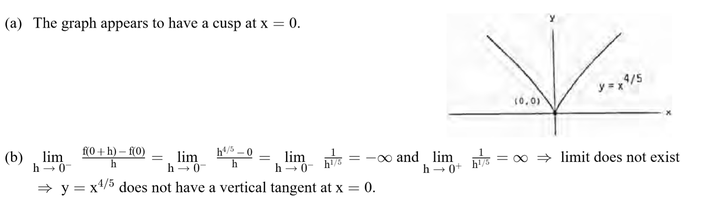
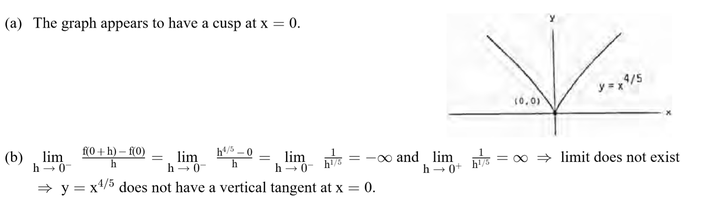
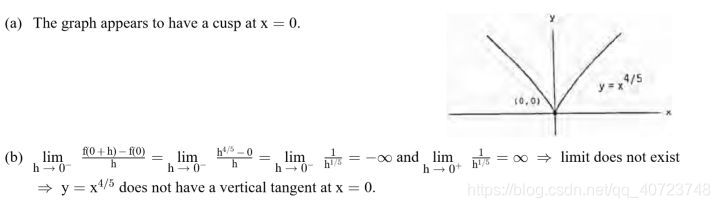

On what intervals are the following functions continuous?


Answer:
![\left[ 0,\infty \right]](https://i-blog.csdnimg.cn/blog_migrate/88e850fca61258753754388a93b856eb.png)

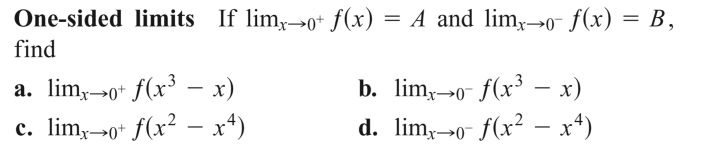
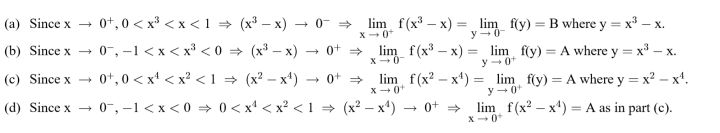







 本文探讨了数学中各种函数的连续性,包括理性函数的斜渐近线、复合函数的连续性条件、指数法则及洛伦兹收缩公式等核心概念。通过具体实例解析,帮助读者理解不同函数在特定点的连续性,并介绍了如何使用极限计算来确认曲线的垂直切线。
本文探讨了数学中各种函数的连续性,包括理性函数的斜渐近线、复合函数的连续性条件、指数法则及洛伦兹收缩公式等核心概念。通过具体实例解析,帮助读者理解不同函数在特定点的连续性,并介绍了如何使用极限计算来确认曲线的垂直切线。

















 3046
3046

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










