线段树（上）

（看了不知道有多久终于看懂的线段树，忍不住想写了）

   线段树，顾名思义，一颗存储线段的树，大致可以这么理解：

将一个1~n的区间通过二分，分成一颗二叉树的形式，对于节点的存储即为tree[i]的左孩子为tree[i*2]，右孩子为tree[i*2+1]，对于每一个节点存储的都是当前这个节点所表示的区间的一些值，且支持单点修改与区间查询，效率是O（log2（n））的。

由此可见线段树在节点上所存储的值必须符合区间加法

符合区间加法的例如：

数字之和——总数字之和=左区间的和+右区间的和

Gcd——总gcd=gcd（左区间gcd，右区间gcd）

最大值——总max=max（左区间max，右区间max）

 

不符合区间加法的例如：

众数——知道左右区间的众数没法求总的众数

最长不下降序列长度——知道左右区间的长度没法求总的长度

由于线段树维护的东西千变万化，所以线段树可以解决很多题目，重点是要会转化。

在开线段树的数组时要开到4N，因为在调用时还会往下一层（虽然是空的，但空间要开好，不然运行时错误）

    

   下面给出线段树分离区间的图（下面讲解会用到）：

 

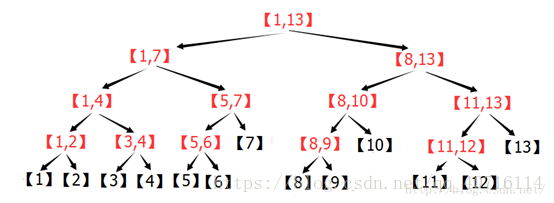
 一段建树并维护最大值的的代码：

#include<bits/stdc++.h>

usingnamespace std;

structSegmentTree{

       int l,r;

       int maxx;

}tree[100001];

int a[100001]={},n;

void build(int x,int y,int k)

{

       tree[k].l=x;tree[k].r=y;

       if (x==y)

        {

             tree[k].maxx=a[x];return ;

        }

       int mid=(x+y)/2;

       build(x,mid,2*k);

       build(mid+1,y,2*k+1);

       tree[k].maxx=max(tree[k*2].maxx,tree[k*2+1].maxx);

}

int main()

{

       scanf("%d",&n);

       for(int i=1;i<=n;i++)

        scanf("%d",&a[i]);

       build(1,n,1);

       for(int i=1;i<=2*n+1;i++)

        {

             printf("%d %d%d\n",tree[i].l,tree[i].r,tree[i].maxx);

        }

}

 

关于线段树的操作：

  单点修改：

     由上图可知，线段树的最后一层每个点都是单个点。那么在修改点时，我们只需要通过判断所需要修改的第i个点，是在当前区间的左区间中还是右区间中，再选择调用，即可找到所需要修改的那个点。再递归返回，一层层修改父亲的值（具体操作由该线段树维护的东西而定）

 Ps:单点修改是一条形似C  I K的指令，意为把a[i]修改为K

 下面给出一段维护最大值的单点修改代码：

void change(int x,int y,int k)

{

       if(x==y&&y==xx)

        {

             tree[k].maxx=yy;return;

        }

    intmid=(x+y)/2;

       if(xx<=mid) change(x,mid,2*k);

       else change (mid+1,y,2*k+1);

       tree[k].maxx=max(tree[2*k].maxx,tree[2*k+1].maxx);

}

 

printf(“%d”,&m);

for(int i=1;i<=m;i++)

{
             scanf("%d%d"&xx,&yy);

  change(1,n,1);

}

时间复杂度为O（logn）

 

   区间查询：

  区间查询是一条形似Q l r的指令，意为查询区间[l,r]中的某个值（如max，gcd，总和等）。对于要查询的区间，我们需要判断这个区间是否完全包含当前节点所代表的区间。如果包含，则以该节点上的值为候选值，并回溯。否则判断它的左右孩子是否与区间[l,r]有重叠部分，如果有，则递归访问该节点。重复上述过程。（起点为根节点）

照例给出一段区间查询最大值的代码：

int ask(int x,int y,int k)

{

       if(l<=tree[k].l&&tree[k].r<=r)

        {

             return tree[k].maxx;

        }

       int mid=(tree[k].l+tree[k].r)>>1;

       int ans=-(1<<30);

       if (l<=mid) ans=max(ans,ask(l,r,2*k));

       if (r>mid) ans=max(ans,ask(l,r,2*k+1));

       returnans;

}Scanf("%d%d",&l,&r);

ask(1,n,1);

时间复杂度为O（logn）

 

 

 

——————————————————上篇完结线—————————————————————