根据提取的相机的参数,2维坐标点转为3维坐标点,代码如下:
import argparse
from argparse import RawTextHelpFormatter
import numpy as np
import cv2
# 寻找焦点
def cam_calib_find_corners(img, rlt_dir, col, row):
# 灰度化图片,减少参数的运算
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 寻找角点
ret, corners = cv2.findChessboardCorners(gray, (col, row), None)
# 为了得到稍微精确一点的角点坐标,进一步对角点进行亚像素寻找
corners2 = cv2.cornerSubPix(
gray, corners, (7, 7), (-1, -1), (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_COUNT, 10, 0.001))
if ret == True:
# 保存角点图像
sav_path = rlt_dir + "/1_corner.jpg"
# 绘制角点
cv2.drawChessboardCorners(img, (col, row), corners2, ret)
cv2.imwrite(sav_path, img)
return (ret, corners2)
# 相机标定
def cam_calib_calibrate(img_dir, rlt_dir, col, row, img_num):
w = 0
h = 0
all_corners = []
patterns = []
x, y = np.meshgrid(range(col), range(row))
prod = row * col
pattern_points = np.hstack(
(x.reshape(prod, 1), y.reshape(prod, 1), np.zeros((prod, 1)))).astype(np.float32)
img_path = r"C:\Users\17930\Desktop\1.jpg"
img = cv2.imread(img_path)
if img is None:
print(f"Error reading image at {img_path}")
pass
else:
(h, w) = img.shape[:2]
ret, corners = cam_calib_find_corners(img, rlt_dir, col, row)
all_corners.append(corners)
patterns.append(pattern_points)
rms, cameraMatrix, distCoeffs, rvecs, tvecs = cv2.calibrateCamera(
patterns, all_corners, (w, h), None, None)
print('相机内参', cameraMatrix)
print('相机外参旋转向量', rvecs)
print('相机外参平移向量', tvecs)
return cameraMatrix, distCoeffs, rvecs, tvecs
if __name__ == "__main__":
parser = argparse.ArgumentParser(
description="读取标定的图片并保存结果", formatter_class=RawTextHelpFormatter)
parser.add_argument("--img_dir", help="标定图片路径", type=str,
metavar='', default=r'D:\螺丝数据集与相机标定代码\camera\calib_img')
parser.add_argument("--rlt_dir", help="保存路径", type=str,
metavar='', default="rlt_dir")
parser.add_argument("--crct_img_dir", help="待矫正图像路径",
type=str, metavar='', default="crct_img")
parser.add_argument("--row_num", help="每一行有多少个角点,边缘处的不算",
type=int, metavar='', default="7")
parser.add_argument("--col_num", help="每一列有多少个角点,边缘处的不算",
type=int, metavar='', default="6")
parser.add_argument("--img_num", help="多少幅图像",
type=int, metavar='', default="4")
args = parser.parse_args()
cameraMatrix, distCoeffs, rvecs, tvecs = cam_calib_calibrate(
args.img_dir, args.rlt_dir, args.row_num, args.col_num, args.img_num)
image_points = np.array([[55, 66], [77, 88]], dtype=np.float32)
world_z = 0
world_points = []
for i in range(len(rvecs)):
rotation_matrix, _ = cv2.Rodrigues(rvecs[i])
projection_matrix = np.dot(cameraMatrix, np.hstack(
(rotation_matrix, tvecs[i])))
inv_projection_matrix = np.linalg.pinv(projection_matrix)
for pt in image_points:
img_pt = np.array([pt[0], pt[1], 1])
ray_dir = np.dot(inv_projection_matrix, img_pt)
scale = (world_z - tvecs[i][2]) / ray_dir[2]
world_pt = tvecs[i].reshape(3) + scale * ray_dir[:3]
world_points.append(world_pt)
world_points = np.array(world_points)
print(world_points)
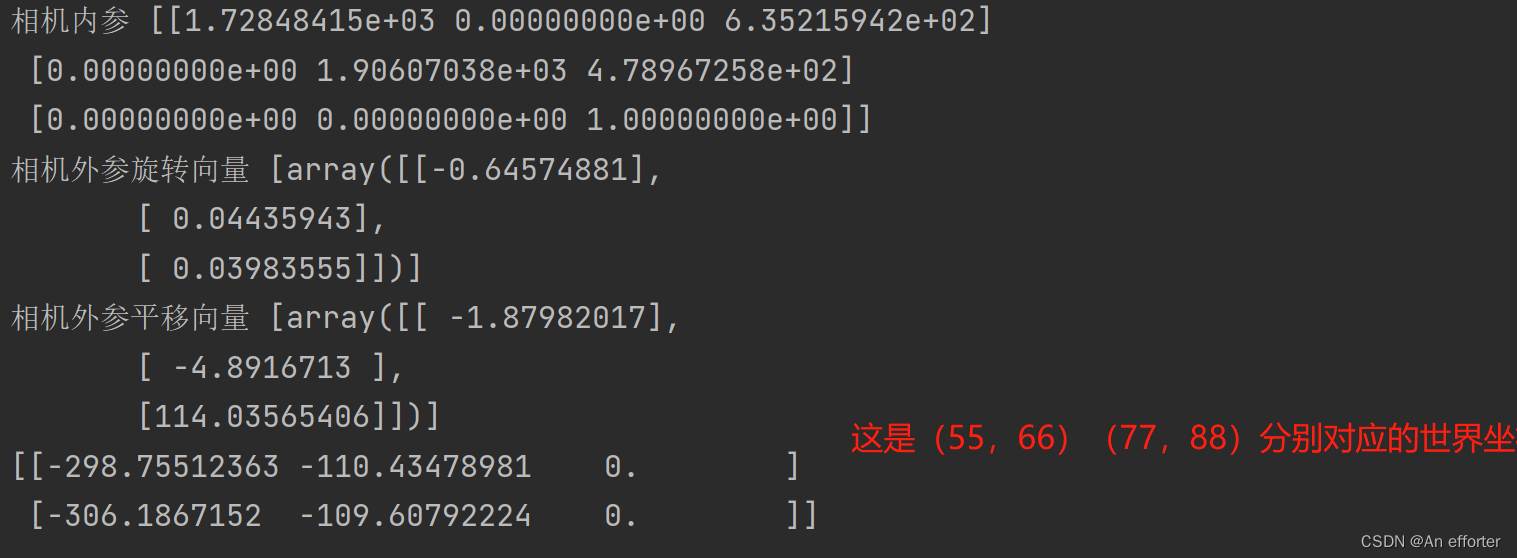







 本文介绍了使用OpenCV进行相机标定和2维坐标点转换为3维坐标的Python函数,包括角点检测、亚像素校准和3D空间重建的过程。
本文介绍了使用OpenCV进行相机标定和2维坐标点转换为3维坐标的Python函数,包括角点检测、亚像素校准和3D空间重建的过程。
















 4380
4380

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








