【课程作业】表达学习 人脸图像复原 实验记录

paper dist: https://ieeexplore.ieee.org/document/4483511
some picture of the blog is taken from teacher’s powerpoint

Prepared Algorithm

范数

OMP(正交匹配跟踪算法)

you can use these blog to learn the main content of the omp(Orthogonal Matching Pursuit) algorithm.

https://zhuanlan.zhihu.com/p/52276805
https://blog.youkuaiyun.com/theonegis/article/details/78230737

SVD(奇异值分解)

you can use these blog to learn the main content of the omp(Orthogonal Matching Pursuit) algorithm.

https://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html
https://www.cnblogs.com/endlesscoding/p/10058532.html

K-SVD

https://zhuanlan.zhihu.com/p/45964374
https://blog.youkuaiyun.com/zhangyake1989/article/details/78366040
https://blog.youkuaiyun.com/theonegis/article/details/78453909

Experiment

本实验具体步骤如下：

• 将数据集划分为训练集和测试集：
  数据集为取37张图片每张图片按8x8的小块划分，将每块reshape为64x1的向量。随机取11000块初始化为数据集（即为64x11000）；取最后一张图像为测试集，同样按8x8的小块划分并置为行数为64的矩阵。

class Divide:
    def __init__(self, b_w, b_h):
        '''
        b_w: block width
        b_h: block height
        '''
        self.block_width = b_w
        self.block_height = b_h

    def encode(self, mat):
        (W, H) = mat.shape
        # (192, 168)->(24,21)
        w_len = int(W / self.block_width)
        h_len = int(H / self.block_height)
        res = np.zeros((self.block_width * self.block_height, w_len * h_len))
        for i in range(h_len):
            for j in range(w_len):
                temp = mat[j * self.block_width:(j + 1) * self.block_width,
                           i * self.block_height:(i + 1) * self.block_height]
                temp = temp.reshape(self.block_width * self.block_height)
                res[:, i * w_len + j] = temp
        return res

    def decode(self, mat, W, H):
        '''
        mat.shape should be ( block_width*block_height, ~ = 24*21 )
        '''
        w_len = int(W / self.block_width)
        h_len = int(H / self.block_height)
        mat = mat.reshape(self.block_width * self.block_height, w_len * h_len)
        
        res = np.zeros((W, H))
        for i in range(h_len):
            for j in range(w_len):
                temp = mat[:, i * w_len + j]
                temp = temp.reshape(self.block_width, self.block_height)
                res[j * self.block_width:(j + 1) * self.block_width,
                    i * self.block_height:(i + 1) * self.block_height] = temp
        return res

• 在训练集上使用$KSVD$算法处理字典。字典大小设计为64x441。

• 对测试集中的人脸像素进行缺失处理（对于图像中每个8x8的小块取部分像素置为0）。

• 在测试集上使用omp算法得到稀疏表达（对于每一列（8x8, 1）的矩阵去除缺失处理过的像素位置，字典同样处理在用omp算法处理），然后使用字典重建图像。

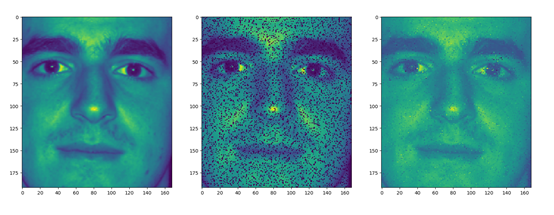
• 计算重建图像与原始图像的平均误差。

与原图像误差：[test_result]:  44.216990942568934
与缺失处理图像误差：[missed_img]:  83.18243391931878

def test_result(B, eva_B):
    '''
    误差计算: 
    error_rate = sqrt(||B - ~B||_2_F / 64)
    '''
    return (np.linalg.norm(B - eva_B))**0.5

Part of Code

读入数据

def read_img():
    '''
    人脸数据集中选取的11000个8 × 8的图像 块（各个部位）
    每一个8 × 8的图像块，是64 × 11000的矩阵𝑌中的一列
    '''
    src_img_w = 192
    src_img_h = 168

    # dataset = np.zeros((38,192,168), np.float)
    dataset = np.zeros((src_img_w * src_img_h, 38), np.float)
    cnt_num = 0
    img_list = sorted(os.listdir(img_path))
    os.chdir(img_path)
    for img in img_list:
        if img.endswith(".pgm"):
            # print(img.size)
            gray_img = cv2.imread(img, cv2.IMREAD_GRAYSCALE)
            # 分块提取 8*8 的 block 汇成矩阵
            # gray_img.reshape(src_img_w * src_img_h, 1)
            divide = Divide(b_w=8, b_h=8)
            gray_img = divide.encode(gray_img)
            # gray_img = cv2.resize(gray_img, (src_img_w, src_img_h),interpolation=cv2.INTER_AREA)
            dataset[:, cnt_num] = gray_img.reshape(src_img_w * src_img_h, )
            cnt_num += 1
    train_data = dataset.reshape(8 * 8, 24 * 21 * 38)
    idx = random.sample(list(range(24 * 21 * (38 - 1))), select_train_num)
    train_data = train_data[:, idx]
    return train_data, dataset[:, -1]

update

def _update_dict(self, y, d, x):
        """
        使用KSVD更新字典的过程
        """
        for i in range(self.n_components):
            # np.nonzero 得到矩阵非0元素位置
            index = np.nonzero(x[i, :])[0]
            if len(index) == 0:
                continue
            # 将第i列清空
            d[:, i] = 0
            # E := Y - D X = Y - Σ(l≠j) d_l X
            r = (y - np.dot(d, x))[:, index]
            # 矩阵的 奇异值 分解
            u, s, v = np.linalg.svd(r, full_matrices=False)
            d[:, i] = u[:, 0].T
            x[i, index] = s[0] * v[0, :]
        return d, x