文章为博主学习Coursera上的Machine Learning课程的笔记,来记录自己的学习过程,欢迎大家一起学习交流
个人博客连接: JMX的个人博客
02:Linear Regression
仍然以房价预测作为示例,具体示例仍需见课程内容。
符号含义:
- m 为数据集的大小
- x’s为输入数据
- y’s为对应的目标输出结果
- (x,y)为所有训练数据
- (xi, yi)为具体第i行数据,第i个训练数据
假设函数h(x),以一元线性回归为例:
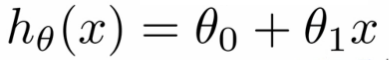
θ
0
:
截
距
θ
1
:
梯
度
\theta_0:截距 \theta_1:梯度
θ0:截距θ1:梯度
Linear regression - implementation(损失函数cost function)
计算由不同θ 取值带来的不同损失函数值,本质上是一个最小化问题:使下式取值最小
M
i
n
i
m
i
z
e
:
(
h
θ
(
x
)
−
y
)
2
Minimize :(h_\theta(x)-y)^2
Minimize:(hθ(x)−y)2
即可以看成下述式子:
J
(
θ
0
,
θ
1
)
=
1
2
m
∑
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
2
J(\theta_0,\theta_1) = \frac 1 {2m}\sum_1^m(h_\theta(x^{(i)})-y^{(i)})^2
J(θ0,θ1)=2m11∑m(hθ(x(i))−y(i))2
1
m
是
求
平
均
1
2
m
是
为
了
数
学
计
算
方
便
\frac1 m 是求平均\frac1 {2m}是为了数学计算方便
m1是求平均2m1是为了数学计算方便
这个损失函数是均方误差,适用于多类回归问题,当然也可以有其他的损失函数。
梯度下降算法(Gradient descent algorithm)
目的: 使损失函数J最小
工作方式
- 从随机初始化开始
- 对θ 随机赋值,可以为任何值
- 每次一点点改变θ,使J(θ)减小
- 每次沿着梯度下降最大的方向
- 重复上述操作直到达到局部最小值
- 从哪里开始的可能决定你到达哪个局部最优解
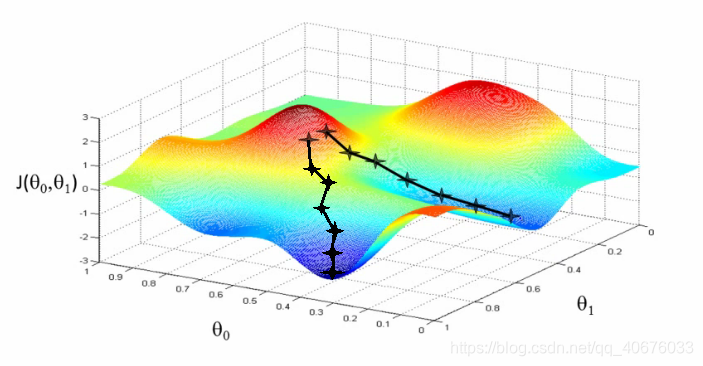
一个更正规的定义:
做下述操作直到收敛:
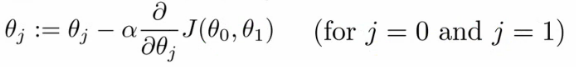
符号解释:
- :=
表示赋值
NB a = b 是一个正确的断言 - α (alpha)
学习率,控制参数更新的步长- 如果学习率过大,可能无法得到最优解,误差会增大
- 如果学习率过小,那么达到最优解需要非常多步,耗费很长时间
注: 参数的更新必须同步即需要一个中间变量保存之前的值,原因是二者的式子中包含了对方,一方的更新会导致第二方式子内值的变化。
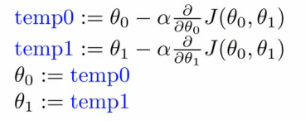
当我们达到局部最优解时:
- 后面部分的梯度为0
- 各参数值就保持不变了
使用梯度下降的线性回归算法
- 将梯度下降算法应用到最小化损失函数J(θ)上
∂
∂
θ
j
=
1
2
m
∑
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
2
=
∂
∂
θ
j
1
2
m
∑
1
m
(
θ
0
+
θ
1
x
(
i
)
−
y
(
i
)
)
2
\frac{\partial} {\partial\theta_j}=\frac 1 {2m}\sum_1^m(h_\theta(x^{(i)})-y^{(i)})^2=\frac{\partial} {\partial\theta_j}\frac 1 {2m}\sum_1^m(\theta_0+\theta_1x^{(i)}-y^{(i)})^2
∂θj∂=2m11∑m(hθ(x(i))−y(i))2=∂θj∂2m11∑m(θ0+θ1x(i)−y(i))2
按照求导公式可以推出:
j
=
0
:
∂
∂
θ
0
J
(
θ
0
,
θ
1
)
=
1
m
∑
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
j=0:\frac{\partial} {\partial\theta_0}J(\theta_0,\theta_1)=\frac1 m\sum_1^m(h_\theta(x^{(i)})-y^{(i)})
j=0:∂θ0∂J(θ0,θ1)=m11∑m(hθ(x(i))−y(i))
j
=
1
:
∂
∂
θ
1
J
(
θ
0
,
θ
1
)
=
1
m
∑
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
∗
x
(
i
)
j=1:\frac{\partial} {\partial\theta_1}J(\theta_0,\theta_1)=\frac1 m\sum_1^m(h_\theta(x^{(i)})-y^{(i)})*x^{(i)}
j=1:∂θ1∂J(θ0,θ1)=m11∑m(hθ(x(i))−y(i))∗x(i)
注:因为线性回归是一个凸函数,是一个碗形的图,所以会趋于局部最优解
- 现在的这种梯度下降算法又叫Batch Gradient Descent 原因是每一次都遍历了整个数据集,后面会提到取数据集中的部分进行的Gradient Descent
- 线性回归也有正规方程求解,但其中矩阵运算当数据集过大时不宜使用,这时就可以使用梯度下降
数值求解的正规方程法
- 直接通过数值求解来避免繁琐的迭代过程,从数学上求解出min(J(θ))
正规方程的优缺点:
优点:
1.不需要学习率这个参数
2.对某些问题可以很快的解决
缺点:
会很复杂
面对数据量很大的时候
这个时候就需要将数据向量化利用线性代数中矩阵运算来完成计算




 本文为Coursera上MachineLearning课程的学习笔记,详细解析了一元线性回归的概念,包括损失函数、梯度下降算法及正规方程法,并探讨了其在房价预测中的应用。
本文为Coursera上MachineLearning课程的学习笔记,详细解析了一元线性回归的概念,包括损失函数、梯度下降算法及正规方程法,并探讨了其在房价预测中的应用。
















 471
471

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








