【Verilog】基于cordic结构的反正切函数

已于 2025-03-04 15:11:03 修改
阅读量338 收藏 5
点赞数 1
文章标签： 算法
于 2025-02-24 14:42:15 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_40629428/article/details/145828615
版权

逐渐把网上的模板代码完善成现在的代码，期间碰到了各种问题，很多时候都是模板代码有问题，真的是很多坑。

一、需求

编写Verilog代码，替换掉工程里的cordic ip核（arctan功能），输入时钟80MHz，输入使能时钟80/6MHz,输入输出数据X、Y宽度均为16位，输出相位角宽度为16位。最终编写的模块和ip核实现的结果进行对比。

一、代码解释

代码中添加了vivado的cordic ip核进行结果的比对，其中ip核的输入输出宽度均为16位，精度为32位。代码文件包括了输入数据的象限初始化、旋转过程、输出结果。
cordic ip核的设置如下所示
在这里插入图片描述
在这里插入图片描述

Cordic_arctan 模块文件如下所示

`timescale 1ns / 1ps
//
// Company: 
// Engineer: ValentineHP
// 
// Create Date: 2025/02/10 22:14:23
// Design Name: 
// Module Name: Cordic_arctan
// Project Name: 
// Target Devices: 
// Tool Versions: 
// Description: 
// 
// Dependencies: 
// 
// Revision:
// Revision 0.01 - File Created
// Additional Comments:
// 
//


module Cordic_arctan #(
        parameter WIDTH = 16,
        parameter ITERS = 16,
        parameter PRECISION = 32
    )(

        input           clk,
        input           rst_n,
		//输入数据的请求使能信号   
        input           cordic_req,
        //输出数据的使能有效信号
        output          cordic_ack,
    
        input signed[WIDTH-1:0]  X,
        input signed[WIDTH-1:0]  Y,
    
        output[WIDTH-1:0]            amplitude,  //幅度，偏大1.64倍，这里做了近似处理
        output  signed[WIDTH-1:0]    theta, 
        //cordic ip核的输出使能和输出角度信号   
        output wire      done_ip,
        output wire signed [WIDTH-1:0] theta_ip
);
	/* 这里注释掉是因为 需要要求输出角度值是16位，
	又因为cordic ip核的输出角度是弧度表示的*/
	// 角度值放大2^16次方
	//`define rot0  32'd2949120       //45度*2^16
	//`define rot1  32'd1740992       //26.5651度*2^16
	//`define rot2  32'd919872        //14.0362度*2^16
	//`define rot3  32'd466944        //7.1250度*2^16
	//`define rot4  32'd234368        //3.5763度*2^16
	//`define rot5  32'd117312        //1.7899度*2^16
	//`define rot6  32'd58688         //0.8952度*2^16
	//`define rot7  32'd29312         //0.4476度*2^16
	//`define rot8  32'd14656         //0.2238度*2^16
	//`define rot9  32'd7360          //0.1119度*2^16
	//`define rot10 32'd3648          //0.0560度*2^16
	//`define rot11 32'd1856          //0.0280度*2^16
	//`define rot12 32'd896           //0.0140度*2^16
	//`define rot13 32'd448           //0.0070度*2^16
	//`define rot14 32'd256           //0.0035度*2^16
	//`define rot15 32'd128           //0.0018度*2^16
	/*因此查找表修改成弧度值表示，从cordic的ip核输出theta_ip数据结构fix16_13，
	最高位表示符号位，theta_ip[14:13]表示整数位，theta_ip[12:0]表示小数位
	可以看出结果是theta_ip放大2^13倍，因此如下表示*/
	//角度的弧度值放大2^13次方
    `define rot0  16'd6433       //45度*2^13
    `define rot1  16'd3798       //26.5651度*2^13
    `define rot2  16'd2006        //14.0362度*2^13
    `define rot3  16'd1018        //7.1250度*2^13
    `define rot4  16'd511        //3.5763度*2^13
    `define rot5  16'd255        //1.7899度*2^13
    `define rot6  16'd128         //0.8952度*2^13
    `define rot7  16'd64         //0.4476度*2^13
    `define rot8  16'd32         //0.2238度*2^13
    `define rot9  16'd16          //0.1119度*2^13
    `define rot10 16'd8          //0.0560度*2^13
    `define rot11 16'd4          //0.0280度*2^13
    `define rot12 16'd2           //0.0140度*2^13
    `define rot13 16'd1           //0.0070度*2^13
    `define rot14 16'd0           //0.0035度*2^13
    `define rot15 16'd0           //0.0018度*2^13
    
    //定义输入数据的寄存器Xn、Yn、Zn
    reg signed[31:0]    Xn[16:0];
    reg signed[31:0]    Yn[16:0];
    reg signed[31:0]    Zn[16:0];
    reg[15:0]           rot[15:0];
    reg                 cal_delay[16:0];
    
    
    assign cordic_ack = cal_delay[ITERS];
    assign theta      = Zn[ITERS];
    //幅度，偏大1.64倍，这里做了近似处理 ,然后缩小了2^15
    assign amplitude  = ((Xn[ITERS] >>> 1) + (Xn[ITERS]  >>> 3) +(Xn[ITERS] >>> 4)) >>> (ITERS-1); 
    
    //实例化cordic_ip
     cordic_0 cordic_atan_inst(
     .aclk(clk),
     .aresetn(rst_n),
     .s_axis_cartesian_tvalid(cordic_req),
     .s_axis_cartesian_tdata({Y,X}),
     .m_axis_dout_tvalid(done_ip),
     .m_axis_dout_tdata(theta_ip)
     );

always@(posedge clk)
begin
    rot[0] <= `rot0;
    rot[1] <= `rot1;
    rot[2] <= `rot2;
    rot[3] <= `rot3;
    rot[4] <= `rot4;
    rot[5] <= `rot5;
    rot[6] <= `rot6;
    rot[7] <= `rot7;
    rot[8] <= `rot8;
    rot[9] <= `rot9;
    rot[10] <= `rot10;
    rot[11] <= `rot11;
    rot[12] <= `rot12;
    rot[13] <= `rot13;
    rot[14] <= `rot14;
    rot[15] <= `rot15;
end

always@(posedge clk or negedge rst_n)
begin
    if( rst_n == 1'b0)
        cal_delay[0] <= 1'b0;
    else
        cal_delay[0] <= cordic_req;
end
//这里输出使能的思路是从输入请求开始因为迭代计算延迟了16个时钟周期
genvar j;
generate
    for(j = 1 ;j < ITERS + 1 ; j = j + 1)
    begin: loop
        always@(posedge clk or negedge rst_n)
        begin
            if( rst_n == 1'b0)
                cal_delay[j] <= 1'b0;
            else
                cal_delay[j] <= cal_delay[j-1];
        end
    end
endgenerate

//将坐标挪到第一和四项限中
always@(posedge clk or negedge rst_n)
begin
    if( rst_n == 1'b0)
    begin
        Xn[0] <= 'd0;
        Yn[0] <= 'd0;
        Zn[0] <= 'd0;
    end
    else if( cordic_req == 1'b1)
    begin
        if( X < $signed(0) && Y < $signed(0))
        begin
            Xn[0] <= -(X << 15);
            Yn[0] <= -(Y << 15);
            //这是-180度的弧度值表示
            Zn[0] <= -16'd25732;
        end
        else if( X < $signed(0) && Y >= $signed(0))
        /*如果输入数据X,Y很小的话，在旋转迭代更新Xn[i]、Yn[i]会有很大的误差，
        因此需要对输入数据进行放大2^15倍处理（网上很多都没有这一步），
        如果2^16倍后续计算会溢出*/
        begin
            Xn[0] <= -(X << 15);
            Yn[0] <= -(Y << 15);
            //这是180度的弧度值表示
            Zn[0] <= 16'd25732;
        end
        else
        begin
            Xn[0] <= X << 15;
            Yn[0] <= Y << 15;
            Zn[0] <= 'd0;
        end
    end
    else 
    begin
        Xn[0] <= Xn[0];
        Yn[0] <= Yn[0];
        Zn[0] <= Zn[0];
    end
end


//旋转迭代更新
genvar i;
generate
    for( i = 1 ;i < 17 ;i = i+1)
    begin: loop2
        always@(posedge clk or negedge rst_n)
        begin
            if( rst_n == 1'b0)
            begin
                Xn[i] <= 'd0;
                Yn[i] <= 'd0;
                Zn[i] <= 'd0;
            end
            else if( cal_delay[i-1] == 1'b1)
            begin
                if( Yn[i-1][31] == 1'b0)
                begin
                    Xn[i] <= Xn[i-1] + (Yn[i-1] >>> (i-1));
                    Yn[i] <= Yn[i-1] - (Xn[i-1] >>> (i-1));
                    Zn[i] <= Zn[i-1] + rot[i-1];
                end
                else
                begin
                    Xn[i] <= Xn[i-1] - (Yn[i-1] >>> (i-1));
                    Yn[i] <= Yn[i-1] + (Xn[i-1] >>> (i-1));
                    Zn[i] <= Zn[i-1] - rot[i-1];
                end
            end
            else
            begin
                Xn[i] <= Xn[i];
                Yn[i] <= Yn[i];
                Zn[i] <= Zn[i];
            end
        end
    end
endgenerate
endmodule

简单的测试文件tb_Cordic_arctan模块如下所示：

`timescale 1ns / 1ps

module tb_Cordic_arctan();

reg clk;
reg rst_n;
reg cordic_req;
wire cordic_ack;
reg signed [15:0] X;
reg signed [15:0] Y;
wire [15:0] amplitude;
wire signed [15:0] theta;
wire done_ip;
wire signed [15:0] theta_ip;

// 实例化被测模块
Cordic_arctan uut (
    .clk(clk),
    .rst_n(rst_n),
    .cordic_req(cordic_req),
    .cordic_ack(cordic_ack),
    .X(X),
    .Y(Y),
    .amplitude(amplitude),
    .theta(theta),
    .done_ip(done_ip),
    .theta_ip(theta_ip)
);

// 生成时钟信号（100MHz）
initial begin
    clk = 0;
    forever #5 clk = ~clk;
end

// 测试逻辑
initial begin
    // 初始化信号

	clk = 0;
    rst_n = 1;
    cordic_req = 0;
    
    #10 rst_n = 0;
    #10 rst_n = 1;    
        
// 测试用例1：验证象限转换 0度       
    #10 cordic_req = 1;
    X = 10;Y = 0;    
    #10 cordic_req = 0; 
// 测试用例2：验证象限转换 45度            
    #40 X = 16'd10;Y = 16'd10;
    #10 cordic_req = 1;
    #10 cordic_req = 0; 
// 测试用例3：验证象限转换 90度            
    #40 X = 16'd0;Y = 16'd10;
    #10 cordic_req = 1;
    #10 cordic_req = 0;        
// 测试用例4：验证象限转换 135度     
    #40 X = -16'd10;Y = 16'd10;
    #10 cordic_req = 1;
    #10 cordic_req = 0;    
// 测试用例5：验证象限转换 180度        
    #40 X = -16'd10;Y = 16'd0;
    #10 cordic_req = 1;
    #10 cordic_req = 0;    
// 测试用例6：验证象限转换 -135度         
    #40 X = -16'd10;Y = -135d10;
    #10 cordic_req = 1;
    #10 cordic_req = 0;
// 测试用例7：验证象限转换 -90度             
    #40 X = 16'd0;Y = -16'd10;
    #10 cordic_req = 1;
    #10 cordic_req = 0;
// 测试用例8：验证象限转换 -45度            
    #40 X = 16'd10;Y = -16'd10;
    #10 cordic_req = 1;
    #10 cordic_req = 0;
    $finish;
end

endmodule

二、运行结果

最终的结果cordic_ack和done_ip需要除以2^13次方得到角度的弧度值，对比两者，输出正确。
在这里插入图片描述

三、补充实验细节

由于简单测试文件只是取每个象限的两个值进行测试，不能有效地检测每一个角度值的正确性。因此需要补充DDS模块，生成正弦信号、余弦信号作为Cordic_arctan的输入数据Y、X，做覆盖性测试。这一步很有必要，发现了对输入数据进行放大2^16倍后续计算会溢出的问题，如图所示。
在这里插入图片描述
因此添加dds_ip模块

module dds_ip(
    input sys_clk,
    input sys_rst_n,
    output  signed[15:0]sin_data,
    output  signed[15:0]cos_data,
    output  [15:0]phase_data,
    output data_valid,
    output phase_valid
    );
    wire [31:0]data;
    assign cos_data={data[15],data[14:0]};
    assign sin_data={data[31],data[30:16]};    
    dds_compiler_0 dds_0(
        .aclk(sys_clk),                                // input wire aclk
        .aresetn(sys_rst_n), // 添加复位信号
        .m_axis_data_tvalid(data_valid),    // output wire m_axis_data_tvalid
        .m_axis_data_tdata(data),      // output wire [31 : 0] m_axis_data_tdata
        .m_axis_phase_tvalid(phase_valid),  // output wire m_axis_phase_tvalid
        .m_axis_phase_tdata(phase_data)    // output wire [15 : 0] m_axis_phase_tdata
    );
endmodule

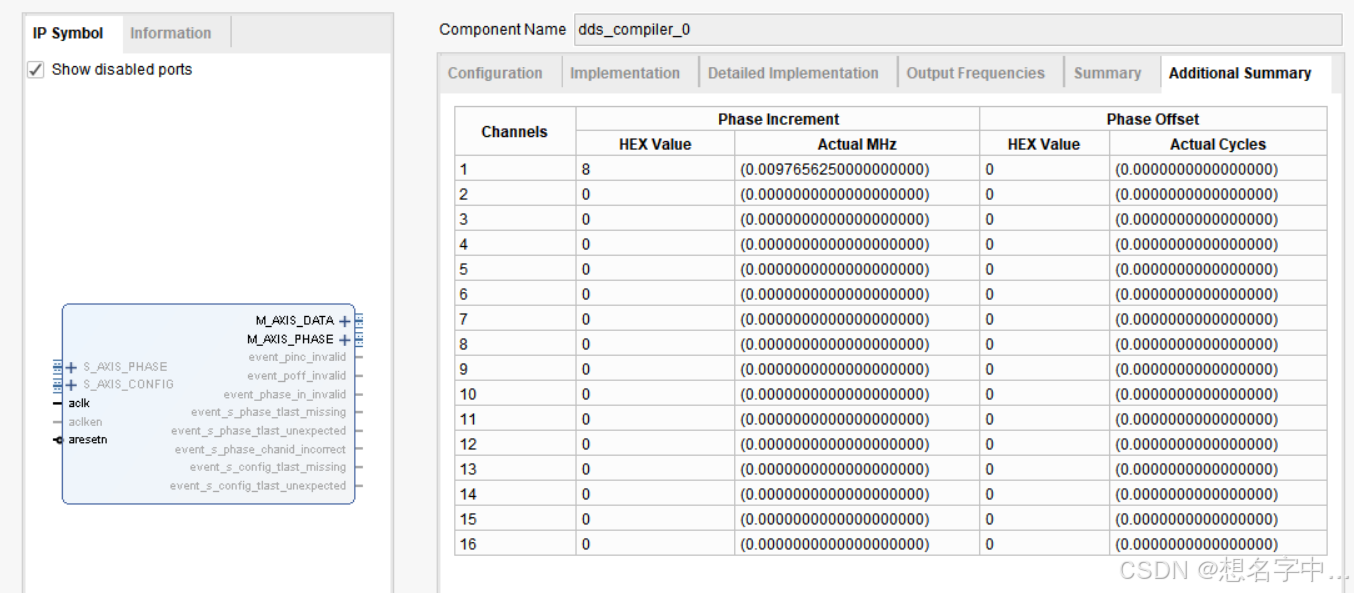
dds ip核相应的设置如下
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
重新编写顶层文件top模块

module top(
    input sys_clk,
    input sys_rst_n,
    input   inrdy,
    output  done,
    output  signed[15:0]    theta,
    output  done_ip,
    output  signed[15:0]    theta_ip,
    output  reg[15:0]          delta
    );
    wire signed[15:0] sin_data;
    wire signed[15:0] cos_data;   
	//这里添加了输出信号delta，切不可眼睛看误差，觉得差不多就行了，严谨看待、数据说话
    always @(posedge sys_clk or negedge sys_rst_n) begin
        if (~sys_rst_n) begin
            delta <= 15'b0;
        end
        else if(done_ip) begin
            delta <= theta - theta_ip;
        end
    end
    //例化dds_ip核
    dds_ip u_dds(
        .sys_clk(sys_clk) ,
        .sys_rst_n(sys_rst_n ),
        .sin_data(sin_data),
        .cos_data(cos_data),
        .data_valid(),
        .phase_valid(),  // output wire m_axis_phase_tvalid
        .phase_data()    // output wire [15 : 0] m_axis_phase_tdata
    );
    //例化cordic_ip核
	 cordic_0 cordic_atan_inst(
        .aclk(sys_clk),
        .aresetn(sys_rst_n),
        .s_axis_cartesian_tvalid(inrdy),
		/*DDS输出的sin_data和cos_data的大概范围为-32768~32768，
		因此需要这里对输入数据算术右移1位，
		是因为cordic_ip核输入数据的范围只能是-1~1；对应16位数据为（-16384~16384）*/
        .s_axis_cartesian_tdata({sin_data>>>1, cos_data>>>1}), 
        .m_axis_dout_tvalid(done_ip),
        .m_axis_dout_tdata(theta_ip)
    );  
    
    //例化反正切模块
    Cordic_arctan uut (
        .clk(sys_clk),
        .rst_n(sys_rst_n),
        .cordic_req(inrdy),
        .cordic_ack(done),
        .X(cos_data),
        .Y(sin_data),
        .amplitude(),
        .theta(theta)
    );
endmodule

重新编写测试文件tb_top如下

`timescale 1ns / 1ps
module tb_top();
    reg sys_clk;
    reg sys_rst_n;
    reg inrdy;
    
    initial begin
        sys_clk<=1'b0;
        sys_rst_n<=1'b0;
        inrdy=0;
        #20
        sys_rst_n<=1'b1;
        
    end
    always begin
        #62.5 inrdy = ~inrdy; // 第一次翻转（间隔62.5）
        #12.5 inrdy = ~inrdy; // 第二次翻转（间隔12.5）
    end
    always #6.25 sys_clk=~sys_clk;
//    always #18.75 inrdy=~inrdy;

    wire done;
    wire [15:0]theta;
    wire done_ip;
    wire [15:0]theta_ip;
   
    top u_top(
        .sys_clk(sys_clk) ,
        .sys_rst_n(sys_rst_n),
        .inrdy(inrdy),
        .done(done),  // output wire m_axis_phase_tvalid
        .theta(theta),    // output wire [15 : 0] m_axis_phase_tdata
        .done_ip(done_ip),
        .theta_ip(theta_ip)
    );
endmodule

最终得到的实验结果，误差信号delta在-6~6，结果正确
在这里插入图片描述

四、遇到的问题

1、精度不够，误差太大
在测试用例(X,Y)=（1，1）、（10、10）时，发现误差太大，由于X、Y的值太小，在旋转过程中，不断的变小或者增大操作使得误差不断累积。联想到X、Y同比例放大不影响最终反正切函数的值，因此可以在初始赋值处，对输入数据X、Y进行左移放大2^15次方。
其次，角度值放大倍数容易造成更大的误差，角度值放大倍数不如弧度值放大倍数，因此查找表改成角度的弧度值放大2^13次方倍。
2、done信号输出错误
解决方法：从输入请求使能计算16个时钟周期后得到输出使能。
3、cordic_ip输出错误，查找发现ip核的输入需要在-1~1之间，通过sin_data>>>1, cos_data>>>1解决问题

FPGA Verilog Cordic算法实现三角函数计算，可计算sin cos arctan，精度达到，10e-5，有完整资料说明
YQQyLQakGe的博客
11-02 3437
该工程包含了Cordic算法模块的Verilog代码和测试文件，同时也提供了详细的资料说明，包括算法原理、模块设计和使用方法等。在未来的工程设计和科研应用中，Cordic算法在FPGA上的实现将具有广泛的应用前景。FPGA在近年来得到越来越广泛的应用，针对三角函数计算的需求，本文提出了一种基于Cordic算法的实现方式。同时，Verilog语言作为FPGA的硬件描述语言，也为Cordic算法在FPGA上的实现提供了很好的支持。Cordic算法是一种迭代算法，主要用于计算三角函数的值。
基于FPGA的CORDIC算法实现——Verilog版
热门推荐
善良の一休君的博客
08-21 6万+
目前，学习与开发FPGA的程序员们大多使用的是Verilog HDL语言（以下简称为Verilog），关于Verilog的诸多优点一休哥就不多介绍了，在此，我们将重点放在Verilog的运算操作上。 我们都知道，在Verilog中，运算一般分为逻辑运算（与或非等）与算术运算（加减乘除等）。而在一开始学习Verilog时，老司机一定会提醒我们，“切记，千万别用‘/’除、‘%’取模（有的也叫取余）和‘
基于Cordic算法求反正切的Verilog及Matlab实现.zip
05-23
本文是根据Cordic算法原理，利用二分法思想，完成对任意输入值求反正切的Verilog编写及Matlab程序仿真，并且自创扩展到四象限，可以求（-180~180）全相位的反正切值，是求反正切非常实用的手段。
FPGA实现CORDIC算法
qq_40052606的博客
07-25 1904
FPGA实现CORDIC算法 CORDIC（Coordinate Rotation Digital Computer）是坐标旋转数字计算机算法的简称，这是一种数学计算的逼近方法，可以通过一系列的加减和移位操作来实现，非常适合计算机硬件实现。在实际运用中常用来求解反正切等三角运算，也就是用在三角函数的运算问题。 CORDIC原理的推导可以在圆周系统下利用旋转模式来实现。 由上图可知向量OP和向量OQ可分别用式1和2表示 利用和差化积公式可得到 把式1带入式3中可知 从式4中可以得到Q点的位置坐标。接下来
Verilog代码之求勾股定理和arctan
qq_16069457的博客
06-30 1147
一段Verilog求反正切模块代码，可以直接仿真再使用。
【【Verilog典型电路设计之CORDIC算法的Verilog HDL 实现】】
weixin_50965981的博客
08-25 1937
Verilog典型电路设计之CORDIC算法的Verilog HDL 实现
基于Verilog的cordic反正切FPGA例程
08-24
总的来说，基于Verilog的CORDIC反正切FPGA例程是一个很好的学习实例，它展示了如何在硬件中实现高效的数学函数计算，这对于理解和设计数字信号处理系统至关重要。通过深入研究和理解这个例程，你可以进一步提升在...
Verilog实现基于Cordic算法的双曲函数计算
06-28
本项目关注的是利用Verilog实现基于Cordic算法的双曲函数计算，特别是双曲正切函数（tanh）。Cordic算法，也称为Volder算法或坐标旋转数字计算机，是一种高效的算法，主要用于实现在有限精度算术下进行复数乘法、除...
cordic算法反正切c语言,Cordic 算法之 反正切
weixin_42504327的博客
05-23 3062
在通信的算法中，常采用Cordic算法之一，知道角度产生正交的的正弦余弦，或者知道正弦和余弦求角度，求反正切。1. 求正弦和余弦值。方法：旋转角度，得到正弦余弦值； 再旋转角度，到达下一个正弦余弦值；直到旋转的角度趋近于 0 ，不能再进行旋转。把每次旋转的坐标的x,Y轴的值各自相加，即得到为该角度的正弦和余弦值。2 .求反正切:Angle = artan(y/x)。方法： 及给定x,y 的坐标...
FPGA Verilog中基于Cordic算法的高精度三角函数计算与串口通信实现
最新发布
05-08
内容概要：本文介绍了利用FPGA和Verilog语言实现Cordic算法进行高精度三角函数(sin、cos、arctan)计算的方法，精度可达10e-5。文中不仅提供了详细的算法解释，还展示了如何将计算结果通过串口发送到PC端查看。整个...
FPGA cordic
08-17
FPGA的cordic算法逻辑，verilog写的。可以用来计算arctan.已在实际接收机项目中使用通过
CORDIC算法Verilog实现，带testbench
07-21
用Verilog实现CORDIC，功能比Xilinx提供的更完善。全并行结构，可计算sin和cos函数
发一个用cordic算法实现取模运算的verilog代码
08-24
发一个用cordic算法实现取模运算的verilog代码 发一个用cordic算法实现取模运算的verilog代码
cordic的verilog实现包含testbench
01-19
用veriolg实现16级流水线结构的cordic加速器，该加速器可求出正弦，余弦值。文件中采用了两种测试机制。一种是从外部读取测试向量；另一种是用循环扫描的方式测试。测试结果都已文件的形式输出，并且在控制台上打印。
Verilog实现CORDIC算法反正切功能及测试代码
在本例中，`cordic_atan.zip`压缩包包含了使用Verilog语言实现的CORDIC算法代码，专注于反正切（arctan）的计算。Verilog是一种硬件描述语言（HDL），广泛用于描述电子系统的硬件结构和行为。 - **源代码**：包含...
Vivado cordic IP核rotate和translate使用详解(附有代码)
m0_66360845的博客
01-10 7135
利用givens旋转可以把一个矩阵分解为一个正交矩阵和一个三角矩阵，在FPGA中要想实现矩阵的上述分解操作，需要用到的就是cordic IP核当中的rotate和translate模式。本文将结合官方的cordic数据手册和自身使用经历详细介绍cordic IP核当中的rotate和translate模式的使用方法。
利用Verilog计算IQ信号相位的一种方法
weixin_46151667的博客
09-27 2219
计算IQ信号相位的一种方式
CORDIC算法在Verilog中的实现
weixin_42430341的博客
05-02 920
CORDIC（Coordinate Rotation Digital Computer）算法，是一种在硬件上实现各种三角函数、双曲函数和幂运算的迭代算法。它由Jack Volder于1959年首次提出，最初用于解决飞行器导航中的坐标旋转问题。该算法的一个显著特点是仅使用加法、减法和位移操作，完全避免了乘法和除法的运算，这使得其特别适合在资源有限的硬件上实现。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值