链表和顺序表的面试题

★★从尾到头打印链表

例如：一个链表是1–>2–>3–>4–>NULL，那么我们打印出来一定是4–>3–>--2>–1>–NULL这样的形式。

方法一：

利用last记录最后一个元素的位置

我们要从尾到头打印，首先我们需要找到链表的尾，也就是最后一个结点，而要找到最后一个结点就是让cur->next==NULL,这样我们就找到了最后一个结点，并且把最后一个数打印出来，那么问题来了，找到了最后一个结点，如何找倒数第二个倒数第三个呢？这就需要我们每次用last记录每次打印的那个元素，这样只要我们用cur->next==last，就可以找到每次要打印的元素了。

代码：

void TailPrint(Node *first)
{//从尾到头打印链表
	Node *last = NULL;//记录最后一个元素的位置
	Node *cur = first;
	while (last!=first)
	{ 
		cur = first;//这里特别注意，每次都要更新cur
		while (cur->next != last)
		{
			cur = cur->next;
		}
			printf("%d-->", cur->data);
			last = cur;
	}
	printf("NULL");
	printf("\n");
}

方法二：

递归

例如：还是一个链表1–>2–>3–>4–>NULL,我们可以先把2,3,4打印出来再打印1，那么2,3,4如何打印呢，我们可以先打印3,4再打印2，要打印3,4先把4打印出来再打印3。很明显，这是一个递归的问题。

代码：

void TailPrint(Node *first)
{
	Node *cur = first;
	if (cur->next != NULL)
	{
		TailPrint(cur->next);
		printf("%d-->", cur->data);
	}
	else
	{
		printf("%d-->", cur->data);
	}
}

★★删除一个无头单链表的非尾结点（不能遍历）

这道题看似无从下手，但却是很简单的，由于是无头链表，我们无法遍历，但是要删除的结点确是知道的，注意，在这里删除的是结点中的数据，因此我们可以通过要删除的结点找到它的下一个结点，将下一个结点的值赋给要删除的这个结点，然后将下一个结点释放。例如：我们要删除1–>2–>3–>4–>5–>NULL中的3，我们首先可以4的值拷贝到3这个位置上即：1–>2–>4–>4–>5–>NULL,然后释放掉后面的4就会变成：1–>2–>4–>5–>NULL。这样就达到了我们想要的效果。代码如下：

void NoHeadNotTail(Node *node)
{//删除一个无头单链表的非尾结点
	Node *next = node->next;//要删除的下一个结点
	node->data = next->data;//复制下一个结点
	node->next = next->next;//删除下一个结点
	free(next);//释放下一个结点
}

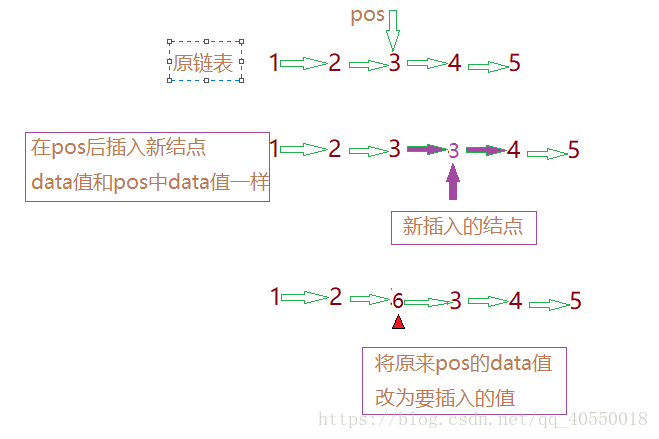
★★在无头单链表的一个结点前插入一个结点（不能遍历）

首先我们可以在pos的后面插入一个结点，并给结点的data值尾pos的data值，再将pos的data值改为要插入的data值，图解如下：

★★单链表实现约瑟夫环（JosephCircle）

约瑟夫环（约瑟夫问题）是一个数学的应用问题：已知n个人（以编号1，2，3…n分别表示）围坐在一张圆桌周围。从编号为k的人开始报数，数到m的那个人出列；他的下一个人又从1开始报数，数到m的那个人又出列；依此规律重复下去，直到圆桌周围的人全部出列。

约瑟夫环运作如下：

约瑟夫环运作如下：
1、一群人围在一起坐成 [2] 环状（如：N）

2、从某个编号开始报数（如：K）

3、数到某个数（如：M）的时候，此人出列，下一个人重新报数

4、一直循环，直到所有人出列 [3] ，约瑟夫环结束

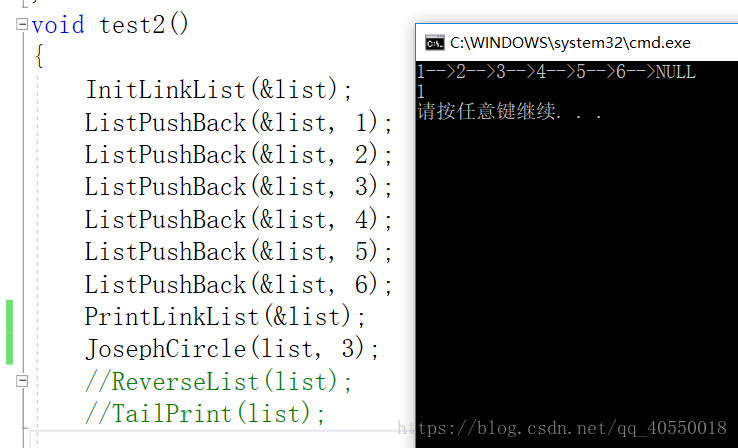
代码如下：

void JosephCircle(Node *first,int k)//报数为k则删除
{
	//构成环
	Node *cur = first;
	while (cur->next != NULL)
	{
		cur = cur->next;
	}
	cur->next = first;
	//删除结点
	cur = first;
	while (cur->next != cur)
	{
		Node *prev = NULL;
		for (int i = 0; i < k - 1; i++)
		{
			prev = cur;
			cur = cur->next;
		}
		prev->next = cur->next;
		free(cur);
		cur = prev->next;
	}
	printf("%d\n", cur->data);
}

★★★★★ 逆置/反转单链表

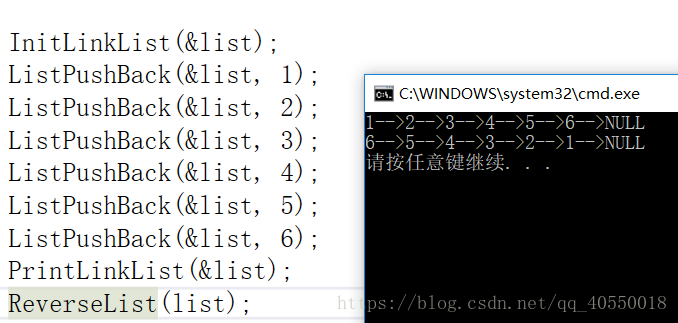
方法一：

我们可以创建一个新的结点，将原来链表中头删一个元素之后然后将这个元素头插到新的结点中，
依次进行头删和头插，例如：原来的链表为：1–>2–>3–>4–>NULL，头删1，再头插到新的结点
中，新的结点就变成1–NULL,而原来的结点就会变成2–>3–>4–>NULL,再将2头删头插…

代码：

void ReverseList(Node *first)
{//逆置/反转单链表
	Node *new = NULL;
	Node *cur = first;//一直指向原链表的第一个结点
	Node *node;
	while (cur != NULL)
	{
		//从原链表头删
		node = cur;
		cur = cur->next;
		//头插到新结点
		node->next = new;
		new = node;
	}
	first = new;//将头插完后的结点放回链表中
	PrintLinkList(&first);//逆置完成后打印

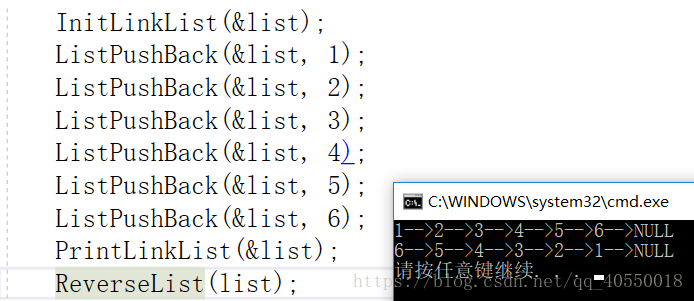
方法二：

原链表是1–>2–>3–>4–>NULL,那么我们逆置之后也可以是NULL<–1<–2<–3<–4

代码：

void ReverseList(Node *first)
{//逆置/反转单链表
	if (first == NULL && first->next == NULL)
	{
		return;
	}
	Node *p1 = NULL;
	Node *p2 = first;
	Node *p3 = first->next;
	while (p2!=NULL)
	{
		p2->next = p1;
		p1 = p2;
		p2 = p3;
		if (p3 != NULL)
		{
			p3 = p3->next;
		}
	}
	PrintLinkList(&p1);//逆置完成后打印
}

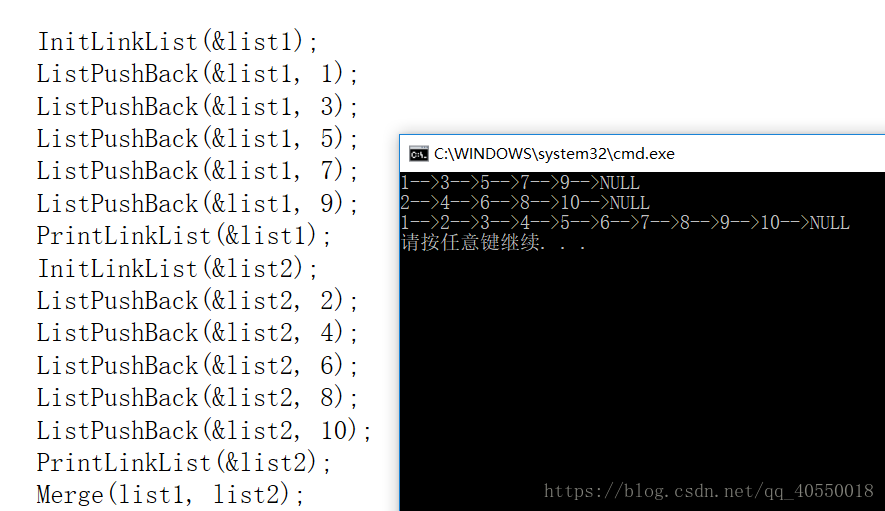
★★★★★合并两个有序链表，合并后依然有序

这里我们需要新建一个result结果链表存放合并后的有序链表，然后分别比较这两个链表的元素，二者当中较小的对它进行头删，并尾插到结果链表中。
代码如下，详情看注释：

void Merge(Node *list1, Node *list2)
{
	Node *cur1 = list1;
	Node *cur2 = list2;
	Node *node;//记录两个链表元素较小的元素
	Node *tail = NULL;//result链表的最后一个结点
	Node *result = NULL;//合并后的链表
	while (cur1 != NULL && cur2 != NULL)
	{
		if (cur1->data <= cur2->data)
		{//比较cur1和cur2，将较小的尾插到result中
			node = cur1;
			cur1 = cur1->next;
            //将node尾插在result中
			if (tail == NULL)
			{
				result = node;
			}
			else
			{
				tail->next = node;
			}
			node->next = NULL;
			tail = node;//更新tail，使得tail始终是result的最后一个结点
		}
		else
		{//比较cur1和cur2，将较小的尾插到result中
			node = cur2;
			cur2 = cur2->next;
			//将node尾插在result中
			if (result == NULL)
			{
				tail = node;
			}
			else
			{
				tail->next = node;
			}
			//更新tail，使得tail始终是result的最后一个结点
			node->next = NULL;
			tail = node;
		}
	}
	//最后必然有一个链表为空了，将不为空的其余元素链到tail后
	if(cur1!=NULL)
	{
		tail->next = cur1;
	}
	if (cur2 != NULL)
	{
		tail->next = cur2;
	}
	PrintLinkList(&result);//最后打印合并后的链表
}

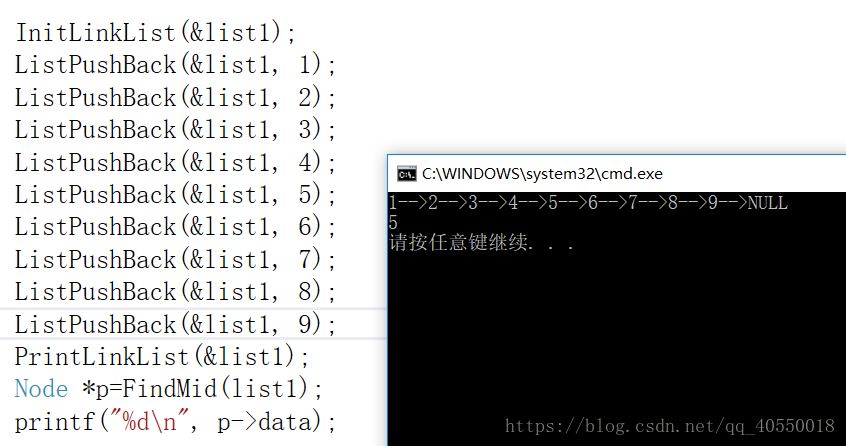
★★查找单链表的中间结点，要求只能遍历一次链表

快慢指针，快的一次走两步，慢的一次走一步，快的走完后慢的刚好指向中间元素

Node *FindMid(Node *list)
{
	Node *fast = list;//快指针
	Node *slow = list;//慢指针
	while (fast)
	{
		if (fast->next != NULL)
		{
			fast = fast->next->next;//快的一次走两步
		}
		else
		{
			break;
		}
		slow = slow->next;//慢的一次走一步
	}
	return slow;
}

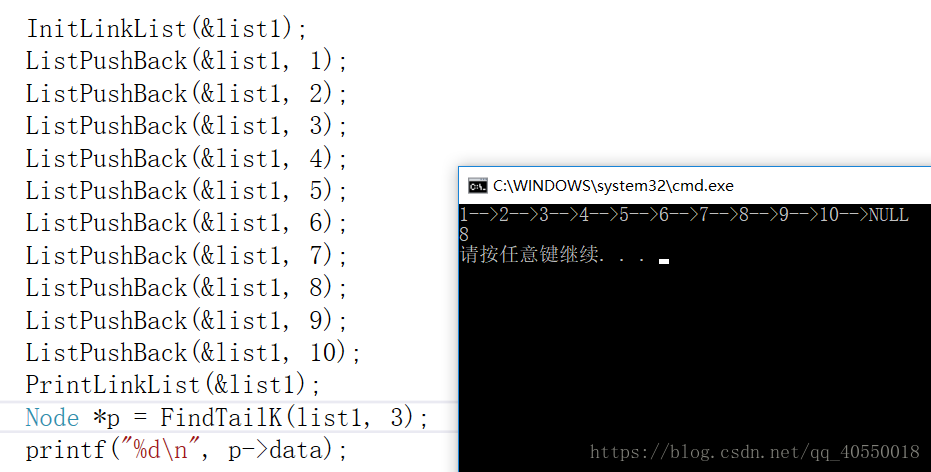
★★查找单链表的倒数第k个结点，要求只能遍历一次链表

定义两个指针，一个先走k步，然后两个同时走，一个走到尾，另一个刚好走到倒数第k个元素

Node *FindTailK(Node *list, int k)
{
	Node *forward = list;
	Node *backward = list;
	while (--k)
	{
		forward = forward->next;//forward先走k步
	}
	while (forward->next)
	{
		forward = forward->next;
		backward = backward->next;
	}
	return backward;
}

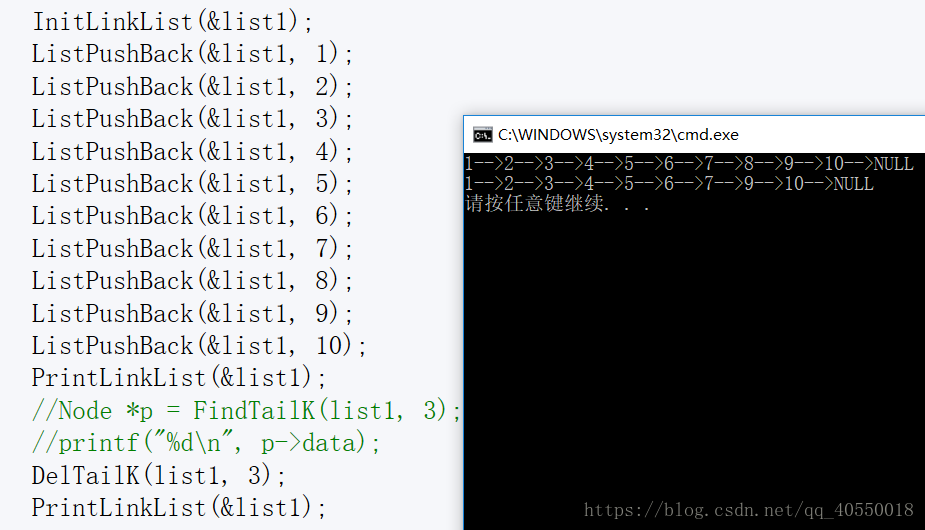
★★删除链表的倒数第k个结点

先找到要删除结点的前一个结点，再删除要删除的结点。

代码：

void DelTailK(Node *list, int k)
{
	Node *node = FindTailK(list, k+1);//找到要删除结点的前一个结点
	if (node == NULL)
	{
		ListPopFront(&list);//如果要删除的结点的前一个结点为空则头删
	}
	else//正常删除
	{
		Node *del = node->next;
		node->next = del->next;
		free(del);
	}
}

★★判断两个链表是否相交，若相交，求交点。（假设链表不带环）

首先我们必须清楚两条链表怎么样才算是相交?是类似于两条线的相交吗？当不然不是，两条链表相交是如下图这样的方式：

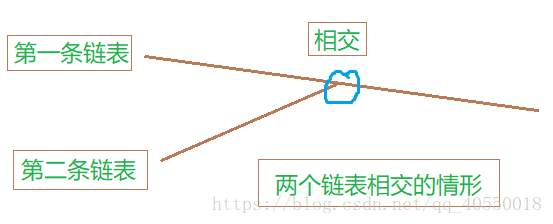
首先我们可以提前算出两个链表的长度，让长的链表先走，走到和短的链表一样长时，再让两个链表同时走，然后分别比较两个链表的每个结点，如果有相等的，则说明有交点，如果走完了也没有相等，则说明无交点

1.先算长度

int GetLength(Node *node)
{//算出链表的长度
	int count = 0;
	while (node != NULL)
	{
		count++;
		node = node->next;
	}
	return count;
}

2.求交点

Node *Crossing(Node *list1, Node *list2)
{//求交点
	int length1 = GetLength(list1);
	int length2 = GetLength(list2);
	Node *longlist = list1;
	Node *shortlist = list2;
	int diff = length1 - length2;//两条链表的长度差
	if(length1<length2)
	{
		longlist = list2;
		shortlist = list1;
		diff = length2 - length1;
	}
	//让长链表先走，走到和短链表一样长
	while (diff--)
	{
		longlist = longlist->next;
	}
	//此时两条链表一样长，再让两条链表同时走
	//如果两条链表的结点相等则有交点
	//如果走完还无交点则无交点
	while (1)
	{
		if (longlist == shortlist)
		{
			return longlist;
		}
		longlist = longlist->next;
		shortlist = shortlist->next;
	}
}