本文详细介绍了贝塞尔曲线的概念、应用以及在Android中实现鼠标拖尾特效的过程。通过创建自定义View，利用贝塞尔曲线算法记录并绘制鼠标轨迹，实现了动态变化的彩色拖尾效果。关键步骤包括计算贝塞尔曲线点、设置计时器更新轨迹、在画布上绘制轨迹线。
特效预览图
什么是贝塞尔曲线？
百度百科：
贝塞尔曲线(Bézier curve)，又称贝兹曲线或贝济埃曲线，是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线，贝兹曲线由线段与节点组成，节点是可拖动的支点，线段像可伸缩的皮筋，我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。
贝塞尔曲线于1962，由法国工程师皮埃尔·贝塞尔（Pierre Bézier）所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau演算法开发，以稳定数值的方法求出贝兹曲线。
贝塞尔曲线是计算机图形图像造型的基本工具，是图形造型运用得最多的基本线条之一。它通过控制曲线上的四个点（起始点、终止点以及两个相互分离的中间点）来创造、编辑图形。其中起重要作用的是位于曲线中央的控制线。这条线是虚拟的，中间与贝塞尔曲线交叉，两端是控制端点。移动两端的端点时贝塞尔曲线改变曲线的曲率（弯曲的程度）；移动中间点（也就是移动虚拟的控制线）时，贝塞尔曲线在起始点和终止点锁定的情况下做均匀移动。注意，贝塞尔曲线上的所有控制点、节点均可编辑。这种“智能化”的矢量线条为艺术家提供了一种理想的图形编辑与创造的工具。本文即用贝塞尔曲线实现鼠标拖尾特效。
理解贝塞尔曲线
贝塞尔曲线数学理解、推导方法：怎么理解贝塞尔曲线？ - 知乎
本文bezier求点公式参考论文：Finding a Point on a Bézier Curve: De Casteljau's Algorithm
引用 贝塞尔曲线简单介绍_xiaozhangcsdn的博客-优快云博客_bezier曲线 对贝塞尔曲线理解关键点进行简要介绍：
对于贝塞尔曲线，最重要的点是数据点和控制点。
数据点： 指一条路径的起始点和终止点。
控制点：控制点决定了一条路径的弯曲轨迹
根据控制点的个数，贝塞尔曲线被分为一阶贝塞尔曲线（0个控制点）、二阶贝塞尔曲线（1个控制点）、三阶贝塞尔曲线（2个控制点）等等。
特点一：曲线通过始点和终点，并与特征多边形首末两边相切于始点和终点，中间点将曲线拉向自己。
特点二：平面离散点控制曲线的形状，改变一个离散点的坐标，曲线的形状将随之改变（点对曲线具有整体控制性）。
特点三：曲线落在特征多边形的凸包之内，它比特征多边形更趋于光滑。
贝塞尔曲线图示
引用自 贝塞尔曲线的数学原理_程序人生-优快云博客_贝塞尔曲线原理
一阶贝塞尔曲线(线段)：
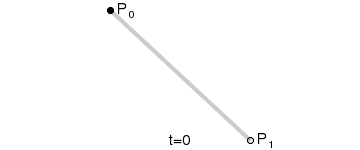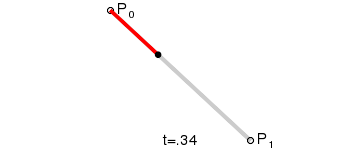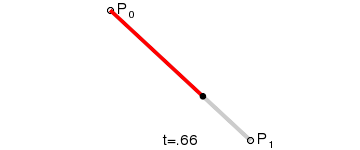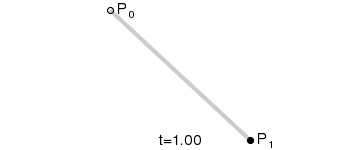
意义：由 P0 至 P1 的连续点， 描述的一条线段
二阶贝塞尔曲线(抛物线)：
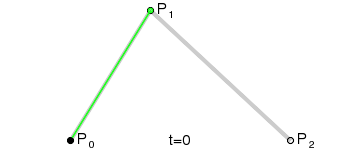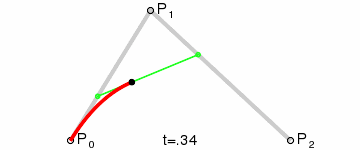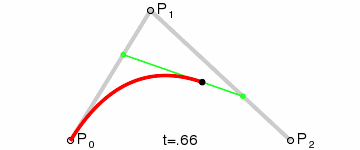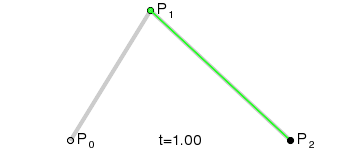
原理：由 P0 至 P1 的连续点 Q0，描述一条线段。
由 P1 至 P2 的连续点 Q1，描述一条线段。
由 Q0 至 Q1 的连续点 B(t)，描述一条二次贝塞尔曲线。
经验：P1-P0为曲线在P0处的切线。
三阶贝塞尔曲线：
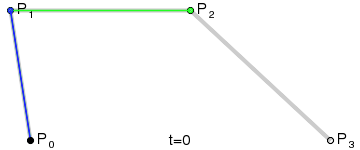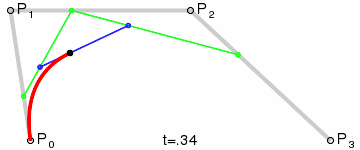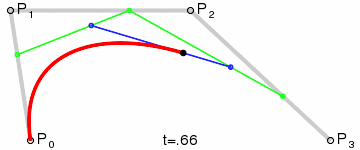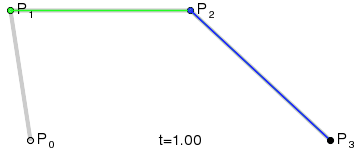
通用公式：
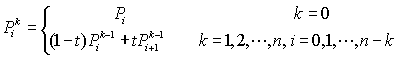
高阶贝塞尔曲线：
4阶曲线：
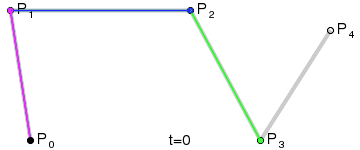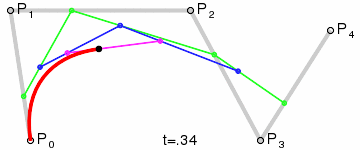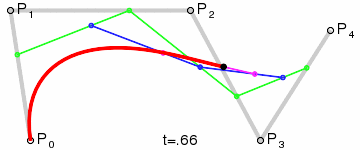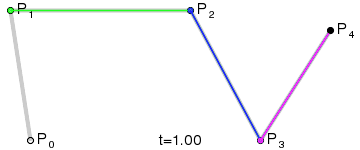
5阶曲线：
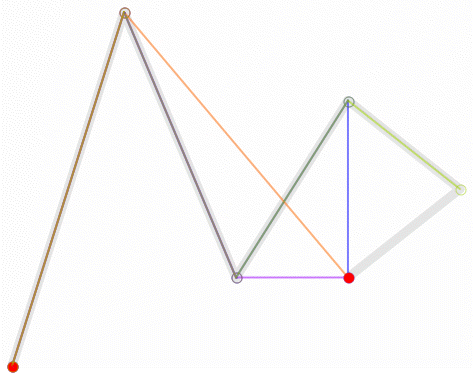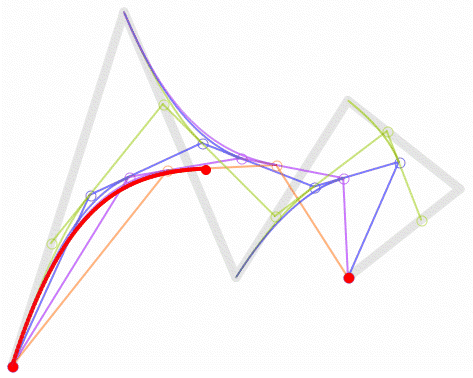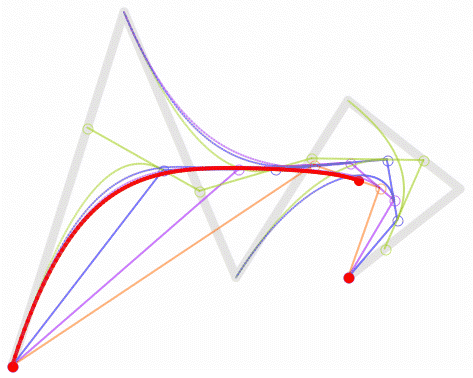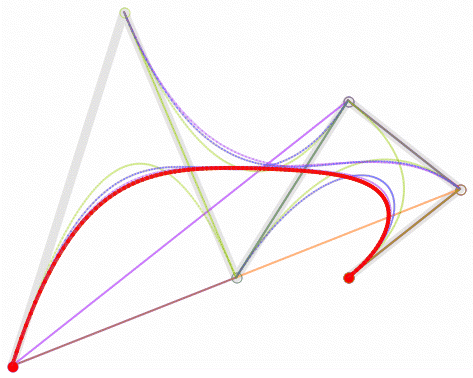
好了，了解完以上贝塞尔曲线的知识，我们该如何用贝塞尔曲线在Android Studio上做特效呢？以本文所提鼠标拖尾特效为例：
第一步
创建新工程
直接创建空白 activity 即可
package com.example.drawimagery;
import androidx.appcompat.app.AppCompatActivity;
import android.os.Bundle;
public class MainActivity extends AppCompatActivity {
@Override
protected void onCreate(Bundle savedInstanceState) {
super.onCreate(savedInstanceState);
setContentView(R.layout.activity_main);
}
}第二步
因为 java 好像并未提供n阶贝塞尔函数的 api，所以我们就自己写一个
创建 Bezier 文件
Bezier 文件作为主函数体文件，保存了 beizer（计算n阶贝塞尔曲线上点的位置）、factorial（阶乘）、rainBow（彩虹色）三个函数。其中贝塞尔曲线公式是运用下图公式计算得出
公式引用自 贝塞尔曲线 WPF MVVM N阶实现 公式详解+源代码下载 - ARM830 - 博客园
- n=有效坐标点数量
- i=坐标点的下标
- P=坐标
- t=时间百分比，在0~1之间，覆盖了整条曲线
因为
可得
硬转换成 java 后其代码如下：
（因为本文项目使用 Queue 进行数据存储所以使用 LinkedList 结构）
package com.example.drawimagery;
import java.util.LinkedList;
public class Bezier {
public static float[] bezier(LinkedList<Float> theArrayX, LinkedList<Float> theArrayY, float t){ //贝塞尔公式调用
float x = 0;
float y = 0;
//控制点数组
int n = theArrayX.size() - 1;
int size = theArrayX.size();
for (int index = 0; index < size; index ++) {
float itemX = theArrayX.get(index);
float itemY = theArrayY.get(index);
if(index == 0){
x += itemX * Math.pow(( 1 - t ), n - index) * Math.pow(t, index);
y += itemY * Math.pow(( 1 - t ), n - index) * Math.pow(t, index);
}else{
//factorial为阶乘函数
x += factorial(n) / factorial(index) / factorial(n - index) * itemX * Math.pow((1 - t), n - index) * Math.pow(t, index);
y += factorial(n) / factorial(index) / factorial(n - index) * itemY * Math.pow((1 - t), n - index) * Math.pow(t, index);
}
}
return new float[] {x, y};
}
public static long factorial(int num) {
if (num < 0) {
return -1;
} else if (num == 0 || num == 1) {
return 1;
} else {
return (num * factorial(num - 1));
}
}
public static int[] rainBow(float t) {
int red, green, blue;
if (t < 0.334) {
red = (int)(255 - t * 3 * 255);
green = (int)(t * 3 * 255);
blue = 0;
} else if (t < 0.667) {
red = 0;
green = (int)(255 - (t - 0.334) * 3 * 255);
blue = (int)((t - 0.334) * 3 * 255);
} else {
red = (int)((t - 0.667) * 3 * 255);
green = 0;
blue = (int)(255 - (t - 0.667) * 3 * 255);
}
return new int[] {red, green, blue};
}
}
Bezier 代码解析
-
public static float[] bezier(LinkedList<Float> theArrayX, LinkedList<Float> theArrayY, float t)：输入鼠标X轨迹、鼠标Y轨迹、所求点在曲线上的位置（百分比表示），返回所求点x，y坐标
-
public static long factorial(int num)：求num的阶乘
-
public static int[] rainBow(float t)：输入彩虹色谱百分比（0~1），返回彩虹色rgb（数组表示）
第三步
创建 MainCanvas 文件
Main Canvas 文件继承自 View ,作为本项目的主画布 view
其代码如下：
package com.example.drawimagery;
import android.content.Context;
import android.graphics.Canvas;
import android.graphics.Color;
import android.graphics.Paint;
import android.os.Handler;
import android.util.AttributeSet;
import android.view.MotionEvent;
import android.view.View;
import java.util.Calendar;
import java.util.LinkedList;
import java.util.Queue;
public class MainCanvas extends View {
private Paint mPaintMouse;//鼠标拖尾画笔
private boolean mouse_begin = false;//鼠标是否按下
private float mouseCurrentX = 0;//当前鼠标位置X
private float mouseCurrentY = 0;//当前鼠标位置Y
Queue<Float> mouseX = new LinkedList<Float>();//保存鼠标轨迹X
Queue<Float> mouseY = new LinkedList<Float>();//保存鼠标轨迹Y
private int time = 0;//累加时间
Handler handler = new Handler();
Runnable runnable = new Runnable() {
@Override
public void run() {
time++;
invalidate();//告诉主线程重新绘制
if (mouseX.peek() != null) {
boolean is_add_mouse = Math.abs(mouseX.peek() - mouseCurrentX) < 0.01;//鼠标不动时不记录坐标
if (!is_add_mouse) {
mouseX.offer(mouseCurrentX);
mouseY.offer(mouseCurrentY);
}
if (mouseX.size() > 20 || is_add_mouse) {
mouseX.poll();
mouseY.poll();
}
} else if (mouse_begin) {
mouseX.offer(mouseCurrentX);
mouseY.offer(mouseCurrentY);
}
handler.postDelayed(this, 20);//每20ms循环一次，50fps
}
};
public MainCanvas(Context context) {
super(context);
}
public MainCanvas(Context context, AttributeSet attrs) {
super(context, attrs);
handler.postDelayed(runnable, 20);
mPaintMouse = new Paint();//对画笔初始化
mPaintMouse.setColor(Color.RED);//设置画笔颜色
mPaintMouse.setStrokeWidth(10);//设置画笔宽度
mPaintMouse.setAntiAlias(true);//设置抗锯齿
}
@Override
public boolean onTouchEvent(MotionEvent event) {//设置触摸事件，手指按下进行记录，手指抬起停止记录
mouseCurrentX = event.getX();
mouseCurrentY = event.getY();
switch (event.getAction()) {
case MotionEvent.ACTION_DOWN:
mouse_begin = true;
break;
case MotionEvent.ACTION_UP:
mouse_begin = false;
break;
}
return true;
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
// int[] color = Bezier.rainBow((float)time % 300 / 300); //画笔同一颜色随时间渐变
int size = mouseX.size();
float x1 = 0,x2 = 0,y1 = 0,y2 = 0;
for (int i = 0; i < size; i++) {
float percent = (float)i / size;
float res[] = Bezier.bezier((LinkedList)mouseX, (LinkedList)mouseY, percent);
x1 = res[0];
y1 = res[1];
if(i == 0){
x2 = x1;
y2 = y1;
continue;
}
int[] color = Bezier.rainBow((time + percent * 300) % 300 / 300); //画笔不同颜色随时间渐变
mPaintMouse.setColor(Color.argb(255, color[0], color[1], color[2]));
mPaintMouse.setStrokeWidth((int)(percent * 20));
canvas.drawLine(x1, y1, x2, y2, mPaintMouse);
x2 = x1;
y2 = y1;
if (i == size - 1) canvas.drawLine(x1, y1, mouseCurrentX, mouseCurrentY, mPaintMouse);//连接最后一段与鼠标
}
canvas.drawCircle(mouseCurrentX, mouseCurrentY, 10, mPaintMouse);//绘制鼠标中心
}
}
Main Canvas 代码解析&思路分析
首先创建所需变量（可将x，y转成一个对象方便操作，这里分开表述比较清晰）
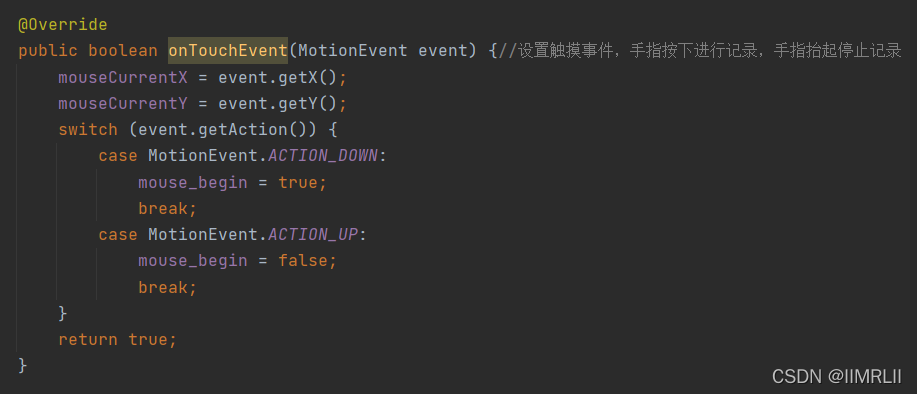然后设置画布触摸事件，每次按下屏幕、滑动屏幕时记录当前鼠标位置，并且设置鼠标按下与抬起事件的标记，方便记录鼠标轨迹。
接着通过 Handler 与 Runnable 的组合实现简单计时器，设定其每20ms循环一次，等同于每秒50帧（这种计时存在较大误差，在这里只是简单实现计时功能，若想精确计时请参考handler实现精确计时的两种方式_王温暖的博客-优快云博客_android handler计时）
然后设置每帧在鼠标移动时对鼠标当前位置进行记录，用鼠标的延迟位置制作鼠标拖尾。数据用 Queue 进行保存，其先进先出的特性十分契合本项目需求。
设置当鼠标拖尾长度 mouseX.size() 大于20后每帧将队列尾部抛出，只保留最多20帧的鼠标拖尾。同时如果鼠标在原地不动时也将队列尾部抛出，这样下次触屏将生成新的贝塞尔曲线。
！！！注意在java中，mouseX.size() 的值不能设置太大。这与我们使用的贝塞尔算法和java的计算机制相关。因为我们是使用阶乘来进行坐标计算，在java中，虽然该阶乘结果数据是作为计算中间值参与运算，但当阶乘的参数n（也就是size）太大时数据仍会溢出（n！>long的范围），造成毁灭性的后果。作者在Lua、JS中的相同算法均未遇到此溢出，猜想是与java的计算方式有关。
然后在画布构建时启动计时器，并且对画笔进行初始化
设置 onDraw 事件进行绘制。简单说就是将之前记录的每帧鼠标轨迹用不同色彩、不同粗细的线段进行连接。这里对几个要点进行说明。
贝塞尔曲线函数接收的参数为鼠标X轨迹、鼠标Y轨迹和所求点在整段曲线的位置（用百分比表示），并以数组形式返回所求点x，y坐标
这段不写鼠标中心与轨迹之间会存在一段空隙
此代码样式演示
此代码样式演示
第四步
修改 activity_main.xml 文件
将我们上文所构建的 View 置入
<?xml version="1.0" encoding="utf-8"?>
<androidx.constraintlayout.widget.ConstraintLayout xmlns:android="http://schemas.android.com/apk/res/android"
xmlns:app="http://schemas.android.com/apk/res-auto"
xmlns:tools="http://schemas.android.com/tools"
android:layout_width="match_parent"
android:layout_height="match_parent"
tools:context=".MainActivity">
<com.example.drawimagery.MainCanvas
android:layout_width="match_parent"
android:layout_height="match_parent">
</com.example.drawimagery.MainCanvas>
</androidx.constraintlayout.widget.ConstraintLayout>OK，运行模拟器，按下鼠标，美丽的贝塞尔曲线-鼠标轨迹就生成啦:)
作者：刘睿
原文链接：https://blog.youkuaiyun.com/qq_40517035/article/details/121882567
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
