动态规划解析

目录

前言

概念——动态规划三要素

最优子结构

无后效性

子问题重叠

解题

题型分类

解题步骤

例题

爬楼梯（70. 爬楼梯 - 力扣（LeetCode） (leetcode-cn.com)）

分析

代码

优化

---

前言

本文是一篇关于动态规划的文章， 也是结合我自己“多次”学习动态规划的血泪史， 写下的一些心路历程和解题思路， 希望对大家有帮助。 当然， 这篇文章是奔着和大家一起探讨的态度写下的， 如果有错误还请直接指出， 一起进步

动态规划学起来比较困难， 与网上很多教程不同的是， 我觉得分析状态转移方程倒是其次的（在难易程度上）， 最重要的是如何分析出这道题是否应该用动态规划，以及动态规划数组下标含义的定义，所以我将尽可能的从这几个方面出发解释一道道例题

---

概念——动态规划三要素

动态规划是否适用于一道题， 有最关键的三个要素， 我们也尽可能分析每一道题是否满足这三要素， 因此这里先对其进行解释

最优子结构

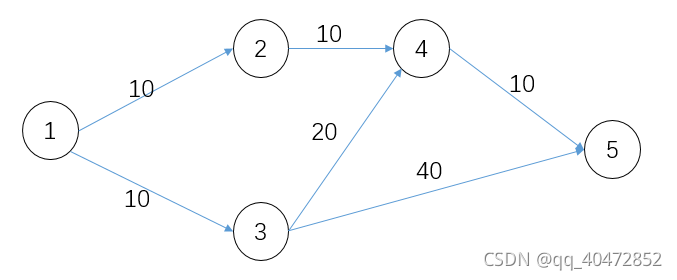
问题最优解所包含的子问题也是最优解。 以最短路径为例来解释， 如下图所示， 从1号节点到5号节点的最短路径是（1 -> 2 -> 4 ->5）。 从最优子结构的定义出发考虑： 4号节点是最优解路径上的节点（也即是子问题）， 那么该最优解中到4号节点也是最优解（从1号节点到4号节点路径最短）

证明（反证法）： 假设最优解路径（1 -> 2 -> 4 ->5）中到4号节点不是最短路径， 那么必有一条路径（1 -> X -> 4） 的距离短于（1 -> 2 -> 4 ）， 则可有（1 -> X -> 4 ->5）的距离短于（1 -> 2 -> 4 ->5）， 则（1 -> 2 -> 4 ->5）不是最短路径， 与题设相矛盾， 故假设不成立

 

无后效性

• 动态规划中子问题的值一旦确定下来， 则此后每一个包含该子问题的大问题的解都只是与该值有关， 而与求出、得到这个子问题的值的方法无关；  
• 动态规划中子问题的值一旦确定下来， 就不受后面更大的问题的影响（即一个问题的计算只与前面更小的问题有关）

我们以爬楼梯（70. 爬楼梯 - 力扣（LeetCode） (leetcode-cn.com)）这道题为例解释无后效性。简单分析一下： 爬楼梯一次只能爬一阶或者两阶， 所以能够到第 i (i > 2)阶楼梯的只能是第 i -