对于网上给出的动态规划找子矩阵最大和的方法的理解

之前在网上看到一个用动态规划找子矩阵最大和的方法(下面有代码链接)

代码链接: https://blog.youkuaiyun.com/wy250229163/article/details/52819403
 

下面是我对这个代码的理解:

1.      首先定义了一个全局变量二维数组num,至于为什么要多出来一行和一列,为什么行和列不是100和100,这个问题在后面解释

 

2.      然后n是测试样例的个数,有几组数据,while循环就几次,这个没什么说的
 

3.      然后他通过memset函数将数组中元素全都初始化为0
 

4.      然后就是我觉得这代码写得很机智的地方了,num数组并不是单纯地用来存储这个二维矩阵的数据的,只能说是暂时存储了二维矩阵中的数据,暂时存进去之后,又立刻对于每一行的每个元素num[i][j],求他在这一列上的前i项和(就相当于以列为单位求前i项和).

也就是说现在的二维矩阵中存储的数据如下所示:(这里以一个5*4的矩阵为例)

(注意代码中i和j都是从1开始遍历的,所以左上角的边缘都是0)

0	0	0	0	0
0	第一列第一个元素	第二列第一个元素	……….	……….
0	第一列前两个元素和	第二列前二个元素和	……….	……….
0	第一列前三个元素和	第二列前三个元素和	……….	……….
0	第一列前四个元素和	第二列前四个元素和	……….	……….
0	第一列前五个元素和	……….	……….	……….

 

         之所以最外面要有半圈的0,是因为在代码中计算每列上的前i项和时是用的累加num[i][j]+=num[i-1][j]的方法,那对于第一行的元素,如果没有最外圈的0,i-1就会使数组下标越界,就要分情况讨论,分为第一行和非第一行进行累加,那就有点麻烦,所以加了半圈0,保证无论哪一行都用相同的方式计算前n项和,这也就是为什么会有步骤1中的101以及步骤3中全部初始化为0的操作
 

5.      接下来就是找最大子矩阵了

遍历子矩阵的思路大致如下:(我们以遍历3*3的矩阵的子矩阵为例)
       

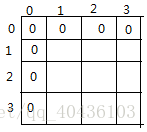
下面我会画出在遍历的过程中都遍历了哪些子矩阵,并在把下标标在旁边

当i=1,j=1时:

           k=1                                                k=2                                                       k=3

                                                                                            

        

                                                                                              

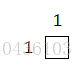
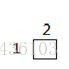
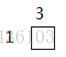
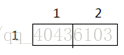
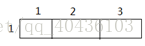
当i=1,j=2时:

             k=1                                    k=2                                                          k=3

                                                                                 

 

                                                              

 

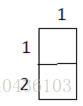
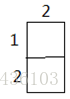
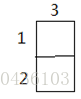
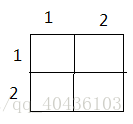
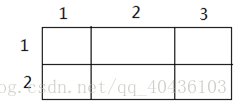
当i=1,j=3时…..(再画一个当i=2,j=2时的,后面就不画了,你们自己画吧)

…………

当i=2,j=2时:

     k=1                                   k=2                                                           k=3

 

                                                                                   

                                                                   

 

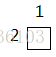
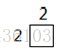
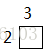
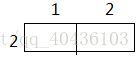
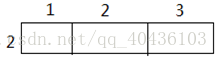
当i=2,j=3时,…….(省略)

 

说明:

         对于temp=num[j][k]-num[i-1][k]和tempmax=(tempmax>=0?tempmax:0)+temp,如果不仔细看的话,好像是按照上述去遍历的,temp求出的就是每种情况第一行的子矩阵的和,tempmax就是每种情况第二行的子矩阵的和(也就是在当前temp的基础上累加上上一次遍历出的结果)

         但是事情并没有这么简单,这不是简单的累加,他加了一个(tempmax>=0?tempmax:0)

(1).这里先解释一下为什么要和0比较(即为什么是个正数才加),试想一下,如果tempmax是一个负数,那tempmax,tempmax+temp和temp中,最大的肯定是temp,因为我们要的是最大的子矩阵和,如果再加负数只会更小,不会更大,再加也不是我们要的最大值,所以当tempmax为负数时,就直接让tempmax=temp,以当前这次遍历的temp为基础进行累加.

(2).其实一开始看这段代码的时候没有仔细考虑,总感觉如果最大子矩阵在中间的话或右下角的话,有的情况可能会遍历不到.

现在,我们再来仔细考虑一下这种情况,如果最大子矩阵在右下角或中间的话,也就是说他左边的几列中的元素是不可能作为最大子矩阵中的元素的,也就是在累加的过程中,原本算在tempmax中的,左边的列的元素”被抛弃掉了”,其实刚好就是(1)中说的情况.即当k遍历到中间的某一列时,发现上一次的tempmax没有这次遍历的temp大,使得tempmax=temp,接下来就以中间的某一次temp为基础遍历累加,就可能会遍历到在中间或右下角的子矩阵了.

 

最后的max=tempmax>max?tempmax:max,这个没什么说的了吧,常规操作,拿上一次遍历中得到的max和这次遍历中找到的最大子矩阵比较.