吴恩达机器学习总结二：单变量线性回归

第二章 单变量线性回归
3、代价函数：（是参数的方程，最常用平方误差代价函数）

定义：也叫损失函数，用来进行参数估计。当用一个确定的方程来拟合一些数据集时，为了保证方程最为合适拟合程度最好，即每一个点的预测值和真实值的差距都要小，故可用求方差的方法，将每一个点的预测值与真实值的差求平方和后再除以数据样本的个数。值越小说明方程越能反映真实情况，把这个方程中的参数看做未知数，则变成了参数的方程，求方程最小值参数即可确定。
4、梯度下降（求让给定多项式取得最小值的参变量的局部最优解）

①比如是二项式有两个变量θ0和θ1，就好像下山一样，先选定一个起点如（θ0=0，θ1=0），此时所在山的高度是f(0,0)，不停寻找下一步斜率最小也即下降最快的方向，最终会来到一个局部最低点，即极值点不一定是最值点，获得一个局部最优解，这个局部最优解跟选择的起点位置相关。
②a:=b表示赋值 a=b表示判定a是否等于b，返回布尔值
③阿尔法叫做学习率，决定了θ值变化的速度。如果θ值过小，梯度下降法迭代的次数会越多；如果过大，可能会一步跨过局部最优值点；其实在趋近最优解的过程中，参数θ的变化是会自动越来越慢的，因为偏导数（偏斜率越来越小），（加上或）减去的那个数不断变小，也就是说变化的越来越少
5、batch线性回归算法：
结合代价函数 和 梯度下降：
①首先确定要用线性方程来拟合：

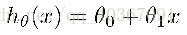
②要求出让这个拟合最准确的参数值，只需让平方误差代价函数的取值最小：

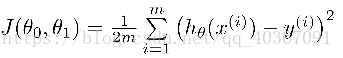
③用梯度下降法找到让代价函数最小的参数θ值

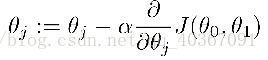
④求解步骤：
将h(x)展开成θ的式子，求偏导


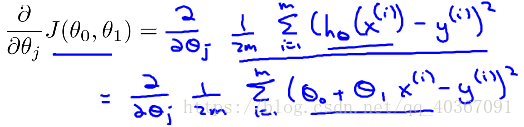
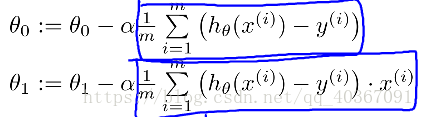
对θ0求导为1，对θ1求导为x(i)
⑤选定一个起点，如θ0=0，θ1=0，带入上式迭代即可