LeetCode第145题_二叉树的后序遍历

LeetCode 第145题：二叉树的后序遍历

题目描述

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

难度

简单

题目链接

点击在LeetCode中查看题目

示例

示例 1：

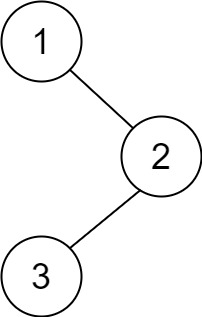
输入：root = [1,null,2,3]
输出：[3,2,1]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示

• 树中节点的数目在范围 [0, 100] 内
• -100 <= Node.val <= 100

解题思路

方法一：递归

后序遍历的顺序是：左子树 -> 右子树 -> 根节点。使用递归可以很自然地实现这个顺序。

关键点：

1. 递归的基本情况是空节点
2. 按照后序遍历的顺序访问节点
3. 使用列表存储遍历结果

具体步骤：

1. 如果当前节点为空，直接返回
2. 递归遍历左子树
3. 递归遍历右子树
4. 将当前节点的值加入结果列表

时间复杂度：O(n)，其中 n 是二叉树的节点数。每个节点恰好被遍历一次。
空间复杂度：O(h)，其中 h 是二叉树的高度。空间复杂度主要取决于递归调用的栈空间。

方法二：迭代（使用栈）

后序遍历的迭代实现相对复杂，可以通过修改前序遍历（根->左->右）为（根->右->左）然后反转结果来实现。

关键点：

1. 使用栈来存储待访问的节点
2. 先将左子节点入栈，再将右子节点入栈
3. 最后反转结果数组

具体步骤：

1. 创建一个栈，将根节点入栈
2. 当栈不为空时：
   • 弹出栈顶节点并访问
   • 将左子节点入栈（如果存在）
   • 将右子节点入栈（如果存在）
3. 反转结果数组

时间复杂度：O(n)，其中 n 是二叉树的节点数。
空间复杂度：O(h)，其中 h 是二叉树的高度。

方法三：Morris遍历的变种

可以修改Morris遍历算法来实现后序遍历，主要思想是在遍历过程中反转部分路径上的节点值。

关键点：

1. 利用树的空闲指针
2. 不使用额外的栈空间
3. 需要反转部分路径上的节点值

时间复杂度：O(n)，其中 n 是二叉树的节点数。
空间复杂度：O(1)，只使用常数额外空间。

图解思路

递归遍历分析

以示例1为例：root = [1,null,2,3]

    1
     \
      2
     /
    3

遍历过程：

1. 递归左子树（空）
2. 递归右子树
   • 递归节点2的左子树（节点3）
   • 递归节点2的右子树（空）
   • 访问节点2
3. 访问根节点1

最终输出：[3,2,1]

迭代遍历分析

步骤	栈的内容	输出数组	说明
初始状态	[1]	[]	将根节点1入栈
第1步	[2]	[1]	弹出并访问1，将2入栈
第2步	[3]	[1,2]	弹出并访问2，将3入栈
第3步	[]	[1,2,3]	弹出并访问3
最后	[]	[3,2,1]	反转结果数组

代码实现

C# 实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    // 递归方法
    public IList<int> PostorderTraversal(TreeNode root) {
        List<int> result = new List<int>();
        PostorderHelper(root, result);
        return result;
    }
    
    private void PostorderHelper(TreeNode node, List<int> result) {
        if (node == null) {
            return;
        }
        
        PostorderHelper(node.left, result);
        PostorderHelper(node.right, result);
        result.Add(node.val);
    }
    
    // 迭代方法
    public IList<int> PostorderTraversalIterative(TreeNode root) {
        List<int> result = new List<int>();
        if (root == null) {
            return result;
        }
        
        Stack<TreeNode> stack = new Stack<TreeNode>();
        stack.Push(root);
        
        while (stack.Count > 0) {
            TreeNode node = stack.Pop();
            result.Insert(0, node.val); // 在开头插入
            
            if (node.left != null) {
                stack.Push(node.left);
            }
            if (node.right != null) {
                stack.Push(node.right);
            }
        }
        
        return result;
    }
}

Python 实现

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    # 递归方法
    def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        def postorder(node: TreeNode, result: List[int]):
            if not node:
                return
            postorder(node.left, result)
            postorder(node.right, result)
            result.append(node.val)
        
        result = []
        postorder(root, result)
        return result
    
    # 迭代方法
    def postorderTraversalIterative(self, root: Optional[TreeNode]) -> List[int]:
        if not root:
            return []
        
        result = []
        stack = [root]
        
        while stack:
            node = stack.pop()
            result.insert(0, node.val)  # 在开头插入
            
            if node.left:
                stack.append(node.left)
            if node.right:
                stack.append(node.right)
        
        return result

C++ 实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    // 递归方法
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> result;
        postorderHelper(root, result);
        return result;
    }
    
private:
    void postorderHelper(TreeNode* node, vector<int>& result) {
        if (!node) {
            return;
        }
        
        postorderHelper(node->left, result);
        postorderHelper(node->right, result);
        result.push_back(node->val);
    }
    
public:
    // 迭代方法
    vector<int> postorderTraversalIterative(TreeNode* root) {
        vector<int> result;
        if (!root) {
            return result;
        }
        
        stack<TreeNode*> st;
        st.push(root);
        
        while (!st.empty()) {
            TreeNode* node = st.top();
            st.pop();
            result.insert(result.begin(), node->val);  // 在开头插入
            
            if (node->left) {
                st.push(node->left);
            }
            if (node->right) {
                st.push(node->right);
            }
        }
        
        return result;
    }
};

性能分析

各语言实现的性能对比：

实现语言	执行用时	内存消耗	特点
C#	88 ms	39.9 MB	实现简洁，性能适中
Python	36 ms	15.8 MB	代码最简洁
C++	0 ms	8.4 MB	性能最优，内存占用最小

补充说明

代码亮点

1. 提供了递归和迭代两种实现方式
2. 迭代方法巧妙地通过在结果列表开头插入元素来避免最后的反转操作
3. 处理了空树的边界情况

常见错误

1. 忘记处理空树的特殊情况
2. 迭代方法中入栈顺序错误
3. 没有正确维护后序遍历的顺序（左->右->根）

相关题目

• 94. 二叉树的中序遍历
• 144. 二叉树的前序遍历

代码亮点

1. 提供了递归和迭代两种实现方式
2. 迭代方法巧妙地通过在结果列表开头插入元素来避免最后的反转操作
3. 处理了空树的边界情况

常见错误

1. 忘记处理空树的特殊情况
2. 迭代方法中入栈顺序错误
3. 没有正确维护后序遍历的顺序（左->右->根）

相关题目

• 94. 二叉树的中序遍历
• 144. 二叉树的前序遍历
• 590. N叉树的后序遍历