优化算法optimization：AdaGrad

最新推荐文章于 2025-06-06 14:49:40 发布

原创最新推荐文章于 2025-06-06 14:49:40 发布 · 521 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#优化算法 #神经网络 #adagrad

Neural Network 专栏收录该内容

22 篇文章

订阅专栏

本文深入解读了AdaGrad算法，介绍了其提出背景，针对梯度不均匀性的解决方案，以及如何通过动态调整学习率来适应不同维度。通过代码示例展示了算法的工作原理，并比较了不同学习率的效果。重点在于理解算法如何在实际问题中提升收敛效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

AdaGrad算法

提出动机

在SGD的每次迭代中，目标函数自变量的每一个元素在相同时间步都使用同一个学习率来进行迭代。我们考虑一个二维输入向量 $x = [x_1,x_2]^T$ 和目标函数$f(x) $。
$x_1 = x_{1} - \eta \frac {\partial f} {\partial x_1} \\\\ x_2 = x_{2} - \eta \frac {\partial f} {\partial x_2}$
由于自变量在不同维度上的梯度不同，我们可以据此调整各个维度上的学习率，从而避免统一的学习率难以适应所有维度的问题。

算法

在时间步 $t$ 使用小批量随机梯度为 $g_t$ 按元素平方的累加变量 $s_t$ ，在时间步0可以初始化 $s_0$ 为0。为了维持数值稳定，我们引入一个常数 $\epsilon$ 。圆圈代表按元素相乘(element-wise multiplication)。对每次迭代做如下改动
$s_t = s_{t-1} + g_t \circ g_t\\\\ x_t = x_{t-1} - \frac{\eta}{\sqrt{s_t+\epsilon}} \circ g_t$
我们仍然用动量法中用来举例的目标函数观察迭代轨迹。

def adagrad_2d(x1, x2, s1, s2, eta=0.4):
    g1, g2 = 0.2 * x1, 4 * x2  ## 自变量梯度
    eps = 1e-6  
    s1 += g1 ** 2
    s2 += g2 ** 2
    x1 -= eta / math.sqrt(s1 + eps) * g1
    x2 -= eta / math.sqrt(s2 + eps) * g2
    return x1, x2, s1, s2

我们将学习率分布为0.4和2的情况进行比较。

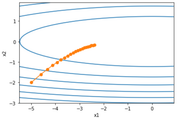
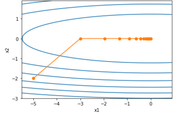
我们发现，学习速率为2的时候快速收敛，并没有发散。

AdaGrad算法在迭代过程中不断调整学习率，并让目标函数自变量中每个元素都分别拥有自己的学习率。使用AdaGrad算法时，自变量中每个元素的学习率在迭代过程中一直在降低（或不变）。

代码实现

def init_adagrad_states(dim=2):
    s_w = np.zeros((dim, 1))
    s_b = np.zeros(1)
    return (s_w, s_b)

def adagrad(params, states, hyperparams):
    eps = 1e-6
    for p, s in zip(params, states):
        s[:] += p.grad * p.grad
        p[:] -= hyperparams['lr'] * p.grad / np.sqrt(s + eps)

Reference

Dive Into Deep Learning，第7章