浅谈机器学习之——支持向量机
最近正准备进行计算机视觉方向的学习,但不知从何入手,决定从机器学习的相关基础知识出发,伴随着相关demo样例的学习。如果有哪位博友大佬恰巧看到这篇博文,还望指点一二(无论是文章内容亦或是计算机视觉相关的学习指导皆可),盼各位大佬不吝赐教。
(注:本文大部分内容来自周志华老师的西瓜书)
如何解决二分类问题?
首先我们来引入一个问题(看图):

问题描述:假定红方块和绿球是两类待分的类别,你能不能用数学的方法将其完全的分开?
1、理想情况:样本完全线性可分
OK,相信看了这个问题的朋友心中都有了自己的答案,这还不简单,画一条直线不就行了吗。Bingo!扩展到三维平面呢?如何将他们分开?想象一下,这个时候我们是不是就要用一个平面才能将其分开。那扩展到多维空间呢,这是我们给它起了一个super响亮的名字——划分超平面。
说到这里,我们来就要引入今天的主角了——支持向量。
在这之前我们还要思考一个问题——既然可以划分出无数多条直线将这两个类别分开那么哪条才是最好的呢?

三秒钟思考一下。。。
ok,俗话说的好,实践是检验真理的唯一标准。你以为我要实验了吗?并没有,我要说的是标准,评价真理需要标准,评价一个事物是好是坏需要标准,回答我们这个问题亦需要标准。那么标准是什么?是不是想到了——距离。
没错,距离,但还不是完全准确。
首先,我们把空间中的划分超平面用数学的方式表现出来:

那么空间中的点到直线的距离就为:

接下来,我们令下式成立:

那么,使上式等号恰好成立的点就是两个类别中各自与超平面距离最近的点。

这个距离之和我们称之为间隔。恰巧使上式等号成立的点我们称之为——支持向量(主角闪亮登场);
间隔即两个异类支持向量到划分超平面的距离之和。

此时我们解决问题的关键就变成找出符合条件的w,也就是6.4的最大值
倒数不好求,这时我们求他的平方的最小值
即:

为了方便求解,我们引入该问题的对偶问题(拉格朗日乘子):

对w和b求偏导:

讲6.9 和 6.10 回带即可得到:


进一步——


此时问题的关键就变成了 求解 α关于接下来具体的求解方法我将在下一篇博文中介绍。(此篇为浅谈,即原理思想性介绍)。
2、较差情况:样本部分线性不可分

如果样本的特征分布情况是这种情况应该怎么办呢?难道我们的支持向量机就不能工作了吗?
其实谈到这里就有两中解决问题的思路:
1、仍然使我们的上式成立,也就是必须找到一个,那么此时我们训练出的分类器就会面临我们最大的敌人——过拟合。
2、允许部分样本不满足式:

在这里,我们引入松弛变量的概念——上式6.3就变成:
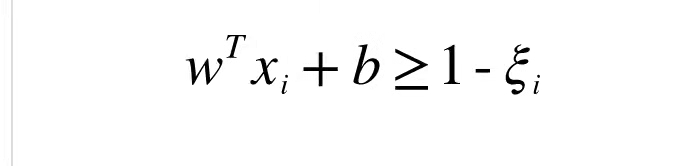
这里我们再引入两个概念——
硬间隔——即第一节所讲 式必须被满足
软间隔——允许部分样本点不满足所给式。即用松弛变量来控制偏离的大小。
3、极差情况:样本完全线性不可分

遇到这种在二维空间并不线性可分的情况该怎么办?
思考三秒钟。。。
是不是可以将其发散一下,有些局部的问题放眼到全局会不会就有一种 拨开乌云见月明的感觉——
说到这里,没错,我们可以将其映射到更高维的空间之后,我们就能够找到一个划分超平面使得其变成线性可分了。就像这样——》

我们将这个映射函数带入到我们的式子中,这时,我们的超平面方程就变成这样:

同样的引入拉格朗日乘子,解得的方程就变为:

但由于我们样本特征向量的维数可能由多维组成,求解多维向量的内积是复杂的。这时,我们想到可不可以找到一个函数,这个函数计算之后的结果恰好就和内积的结果相等呢?我们就把这个函数成为核函数。引入核函数之后的式子变成了这样。

ok,上述内容就是浅谈支持向量机的全部内容了。关于具体的算法以及细节相关的知识,我将在后续的博文中为大家一一介绍。如本文的叙述顺序和内容有何纰漏还望各位博友不吝赐教。鄙人在此谢过了。








 本文介绍了支持向量机(SVM)的基础知识,包括如何解决二分类问题,尤其是处理线性可分和不可分样本的情况。在理想情况下,通过寻找最大间隔的超平面来划分样本;当样本线性不可分时,引入了松弛变量和软间隔概念。此外,针对非线性问题,SVM通过映射到高维空间并利用核函数实现线性可分。本文是SVM的初步探讨,后续会深入讨论算法细节和具体实现。
本文介绍了支持向量机(SVM)的基础知识,包括如何解决二分类问题,尤其是处理线性可分和不可分样本的情况。在理想情况下,通过寻找最大间隔的超平面来划分样本;当样本线性不可分时,引入了松弛变量和软间隔概念。此外,针对非线性问题,SVM通过映射到高维空间并利用核函数实现线性可分。本文是SVM的初步探讨,后续会深入讨论算法细节和具体实现。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








