机器学习-001-SVM线性可分-2020-4-28_使用svm分类方法对线性可分数据集进行分类训练线性可分数据集的svm模型,然后用训-优快云博客

SVM(support vector machine)支持向量机

二分类模型：

特征空间上的间隔最大线性分类器，这点跟感知机不同。
通过核技巧，变成非线性分类器
求解算法，凸二次规划的最优算法( 运筹学 )

模型简单到复杂：

线性可分支持向量机 Linear support vector machine in linearly separable case 又称硬间隔支持向量机（训练数据集线性可分,通过硬间隔最大化 hard margin maximization）
线性支持向量机 Linear support vector machine （训练数据集近似可分时，通过软间隔最大化 soft margin maximization）
非线性支持向量机 Non-linear support vector machine （训练数据集线性不可分，通过核技巧，kernel trick ，及软间隔最大化）

数据集：

数据集是线性可分的

其中，，，为第个特征向量，标签，当它等于+1时为正例；为-1时为负例

支持向量：离超平面最近的点为支持向量，（如下图，在虚线上的点就是支持向量）

支持向量(带圆圈的点)，离超平面尽可能远，就能保证所有的正反例离这个超平面尽可能的远。

原始问题1：

（s.t subject to 限制条件）

原始问题来由？

一个线性可分的数据集: ∀i ∈(1,n),ョ(w,b)有

简写：yi(wTxi + b) > 0 (合并上面两个等式)

点到平面的距离：任意一点到超平面为wTx+b=0 直线距离 d

函数间隔（functional margin）一个样本x，|wTx+b|表示点x到超平面的距离，通过观察wTx+b和y是否同号，我们判断分类是否正确所以定义函数间隔：

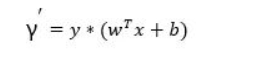
相当于|wTx+b|

几何间隔（geometrical margin）就是在函数间隔的基础下，在分母上对w加上约束，就是点到直线的距离

我们知道当同时扩大w和b，分子分母都会同样扩大，对目标函数不影响，所以在这里我们将分子(支持向量到超平面的函数间隔)扩大或压缩等于1即是

|wTx+b| =1

目标函数进一步化简：

所以得到原问题。

我们只关心支持向量上的点。随后我们求解d的最大化问题变成了||w||的最小化问题。进而||w||的最小化问题等价于

于是就得到下面的线性可分支持向量机学习的最优化问题

原始问题2：

现在的目标函数是二次的，约束条件是线性的，是一个凸二次规划（convex quadratic programming）

能不能将目标函数和约束条件联列成一个式子（拉格朗日乘子法）

从而将有约束优化问题转换为无约束优化问题。

在拉格朗日优化的问题上，需要进行下面二个步骤：

将有约束的原始目标函数转换为无约束的新构造的拉格朗日目标函数
使用拉格朗日对偶性，将不易求解的优化问题转化为易求解的优化

给每一个约束条件加上一个拉格朗日乘子（Lagrange multiplier）

=(1,2,..n)T 为拉格朗日乘子向量

现在我们令

当样本点不满足约束条件时，即在可行解区域外：

此时，将设置为无穷大，则也为无穷大。

当满本点满足约束条件时，即在可行解区域内：

此时，为原函数本身。于是，将两种情况合并起来就可以得到我们新的目标函数

建立了一个在可行解区域内与原目标函数相同，在可行解区域外函数值趋近于无穷大的新函数。

于是原约束问题就等价于 (先极大化L(w,b,) , 在极小化)

p*表示这个问题的最优值

新目标函数，先求最大值，再求最小值。首先求解的是参数和的方程，而又是不等式约束，这个求解过程不好做。所以，我们需要使用拉格朗日函数对偶性，将最小和最大的位置交换一下，这样就变成了：

最优值用d*来表示

对偶问题是极大极小问题，就是先极小化L(w,b,) 对w,b，再在极大化对

定理：，d*<=p*（这是一条定理）

原问题的解带入目标函数值 p* 大于等于对偶问题的解带入对偶问题的值 d*(定理使用即可，不要问为什么? ) 证明在svm_非线性可分笔记中

间距（Dualty Gap)

G = p* -d*

G叫做原问题与对偶问题的间距，对于特定的优化问题，可以证明G = 0 ，

G = 0 ，要有，需要满足两个条件：

优化问题是凸优化问题（显然满足）
满足KKT条件

KKT条件的全称是Karush-Kuhn-Tucker条件，KKT条件是说最优值条件必须满足以下条件：

条件一：经过拉格朗日函数处理之后的新目标函数L(w,b,α)对α求导为零：
条件二：h(x) = 0；
条件三：α*g(x) = 0；

假设我们的优化问题满足KKT条件，优化问题中没有h(x) = 0等式条件 ,只有下面这几个

求对偶问题的极小化

首先固定α，让关于w和b最小化, 分别求和的偏导数，令其等于0，可得

将上述结果带回L(w,b,α)得到：消去和，

即求得 w,b 最小化：

此时的L(w,b,α)函数只含有一个变量，即αi

再求对的极大值，即是对偶问题

把目标式子加一个负号，将求解极大转换为求解极小

转化问题3：

现在的优化问题变成了如上的形式。

对于这个问题，有更高效的优化算法，即序列最小优化（SMO）算法。通过SMO优化算法能得到，再根据，我们就可以求解出和，进而求得我们最初的目的：找到超平面，即”决策平面”。

总结:

上面推导就是将最初的原始问题，转换到可以使用SMO算法求解。

前面的推导都是假设满足KKT条件下成立的，KKT条件如下

另外，根据前面的推导，还有下面两个式子成立

由此可知在中，至少存在一个（反证法可以证明，若全为0，则，矛盾），对此有

因此可以得到

对于任意训练样本，要么或者

当，则该样本不会在最后求解模型参数的式子中出现。

若，则必有，所对应的样本点位于最大间隔边界上，是一个支持向量。

训练完成后，大部分的训练样本都不需要保留，最终模型仅与支持向量有关。

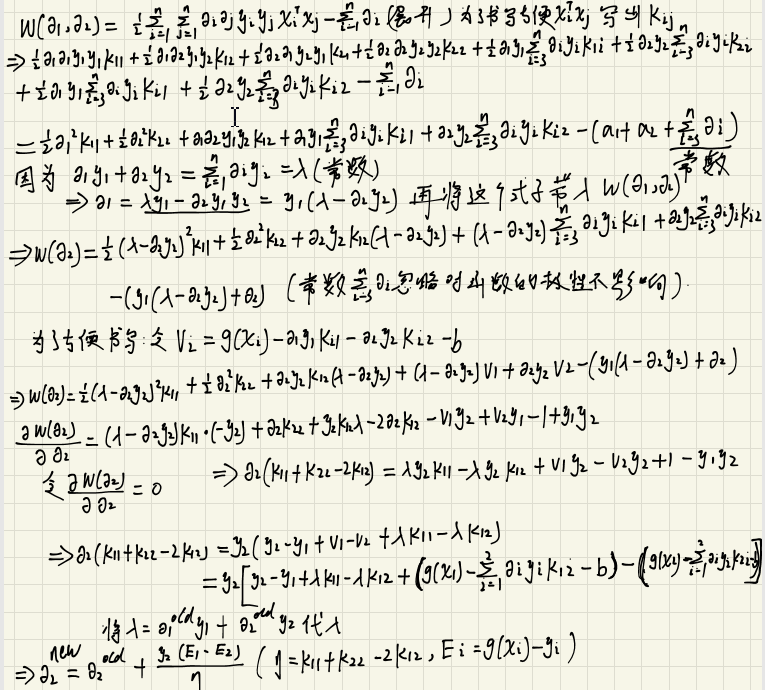
代码实现：(人工制造一个线性可分的数据集，利用smo算法求出决策面)

1 ：smo 每次迭代随机选择一个参数aphaJ

2: smo 选择max abs(Ei - Ej ) 最大，可以加快计算速度

参数要适当调整，程序还有问题。有时候感觉分的不好！C=0.6效果感觉还不错，C越小，越难看！！！toler大小范围对结果影响有点不明显。

3: sklearn 实现svm,

import numpy as np import matplotlib.pyplot as plt# 产生一个线性可分的数据集def makeLinearSeparableDateSet(NormalVector,numpoints=100):    """    NormalVector : 是一个列表，存储的是产生随机数据那条的直线的法向量    numpoints : 模拟数据集中的数据点个数     Randomly generate numlines points on both sides of the    hyperplane :  NormalVector * x  =0    notice: NormalVector and x are vectors    return  a linear Separable data set .    """    w = np.array(NormalVector)      # w ：vector 法向量的垂线    numFeatures = len(NormalVector) #  产生每条数据 特征的数量，几个特征    dataSet = np.zeros((numpoints,numFeatures+1)) #产生一个全0 矩阵 ,numFeatures  +1是标签    for i in range(numpoints):        x = np.random.rand(1,numFeatures) # 产生 1*numFeatures 符合N(0,1)        x = x*20-10        innerProduct = np.sum(w*x)     # 注意w*x是叉乘，不是矩阵乘法         if innerProduct <=0 :          # w*x <0 ，负分类点            dataSet[i] = np.append(x,-1)        else :            dataSet[i] = np.append(x,1)    return dataSetdef selectRand_j(i, m):    """     随机选择一个j ,与i 不同     i ：alpha[i]     m :  训练数据的个数      """    j = i                   #选择一个不等于 i的 j    while (j == i):        j = int(np.random.uniform(0, m))    return jdef clipAlpha(aj,H,L):    """    修剪alpha        aj - alpha[j]的值        H：alpha[j]上限        L：alpha[j]下限    Returns:        aj - alpah[j]修剪值    """    if aj > H:        aj = H    if L > aj:        aj = L    return aj"""smo简单算法实现， 随机选择alpha[i] ,alpha[j],固定其他alpha[],在kkt条件下更新alpha[j] ,在更新alpha[i]，直到所有alpha第满足限制条件"""def smoRand(x, y, C, toler, epochs):    """    函数说明:简化版SMO算法    x : 数据矩阵    y : 数据标签    C : 松弛变量    toler : 容错率    epochs : 最大迭代次数        """     #转换为numpy的矩阵存储    x = np.mat(x)     y = np.mat(y).transpose() # 标签变成 [m,1] 矩阵      m,n = np.shape(x)    #初始化b参数    b = 0    #初始化alpha参数，设为0    alphas = np.mat(np.zeros((m,1)))    #初始化迭代次数    epoch_num = 0    #最多迭代epochs次    while (epoch_num < epochs): #迭代epochs轮，alpha没有改变，就结束循环        alphaChanged = 0  # 记录alpha是否改变        for i in range(m):       # 选择第一个变量alpha[i] 为外循环变量            #计算误差Ei            Ei = float(np.multiply(alphas,y).T*(x*x[i,:].T)) + b -y[i]            # 检测i这个样本点如果为支持向量，是否满足kkt条件，不满足，优化alpha            if ((y[i]*Ei < -toler) and (alphas[i] < C)) or ((y[i]*Ei > toler) and (alphas[i] > 0)):                #i不满足kkt,条件随机选择另一个与alpha[i]成对优化的alpha[j]                j = selectRand_j(i,m)                #计算误差Ej                Ej = float(np.multiply(alphas,y).T*(x*x[j,:].T)) + b -y[j]                #保存更新前的aplpha值，使用深拷贝                alphaIold = alphas[i].copy()                alphaJold = alphas[j].copy()                #计算上下界L和H                if (y[i] != y[j]):                    L = max(0, alphaJold - alphaIold)                    H = min(C, C + alphaJold - alphaIold)                else:                    L = max(0, alphaJold +alphaIold - C)                    H = min(C,  alphaJold +alphaIold)                #计算eta k11 + k22 -2k12                eta =  x[i,:]*x[i,:].T + 1.0*x[j,:]*x[j,:].T-2.0 * x[i,:]*x[j,:].T                if eta == 0:                   # 除数不能为0                    continue                #更新alpha[j]                alphas[j] = alphaJold+y[j]*(Ei - Ej)/eta                #修剪alpha[j]                alphas[j] = clipAlpha(alphas[j],H,L)                if (abs(alphas[j] - alphaJold) < 0.00001):                    #alpha_j变化太小,跳出这次循环                    continue                #更新alpha[i]                #公式  alphaIold =C*yi -alphaJold*yiyj    alpha[i]_new = c*yi -alpha[j]_new*yiy2j 两个式子相减                alphas[i] += y[j]*y[i]*(alphaJold - alphas[j])                #更新b1和b2                b1 = b - Ei- y[i]*(alphas[i]-alphaIold)*x[i,:]*x[i,:].T - y[j]*(alphas[j]-alphaJold)*x[i,:]*x[j,:].T                b2 = b - Ej- y[i]*(alphas[i]-alphaIold)*x[i,:]*x[j,:].T - y[j]*(alphas[j]-alphaJold)*x[j,:]*x[j,:].T                #根据b1和b2更新 b                if (0 < alphas[i]) and (C > alphas[i]):                     b = b1                elif (0 < alphas[j]) and (C > alphas[j]):                     b = b2                else:                    b = (b1 + b2)/2.0                #统计优化次数                alphaChanged += 1                #打印统计信息                #print("本次迭代样本点:%d, alpha优化次数:%d" % (i,alphaChanged))        #更新迭代次数        if (alphaChanged == 0):  #alpha没有改变，轮数+1，否则重新迭代            epoch_num += 1        else:             epoch_num = 0    return b,alphasdef get_w(x, y, alphas):    alphas= np.array(alphas)    x = np.array(x)    y = np.array(y).reshape(1, -1).T # 将y 变成 m*1 [y]    res =np.tile(y,(1, 2)) * x #np.title,将y 扩展成 m*2 [y,y]    w = np.dot(res.T, alphas)    return w.tolist()""" 图像可视化"""def showDataSet(dataSet,w,b,alphas):    ax = plt.subplot(1,1,1,facecolor='white')    ax.set_title("SVM")    plt.xlabel('X')    plt.ylabel('Y')    labels = dataSet[:,2]         # 获得 数据集的标签    idx_1 = np.where(dataSet[:,2] == 1 )  # 找出数据集中标签为 1 的下标    p1 = ax.scatter(dataSet[idx_1,0],dataSet[idx_1,1],marker='o',color='g',label=1,s=20)    idx_2 = np.where(dataSet[:,2] == -1)    p2 = ax.scatter(dataSet[idx_2,0],dataSet[idx_2,1],marker='x',color='r',label=-1,s=20)    #绘制决策面直线    data=dataSet[:,0:2]    x1 = max(data[:,0])    x2 = min(data[:,0])    a1, a2 = w    b = float(b)    a1 = float(a1[0])    a2 = float(a2[0])    y1, y2 = (-b- a1*x1)/a2, (-b - a1*x2)/a2    plt.plot([x1, x2], [y1, y2])    #找出支持向量点 alpha != 0     for i, alpha in enumerate(alphas):        if abs(alpha) > 0:            x, y = data[i]            plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')    plt.legend(loc = 'upper right')    plt.show()#获得一个数据集dataSet = makeLinearSeparableDateSet([3,4],15)x = dataSet[: ,0:2]  # 训练数据y = dataSet[: ,-1]   # 训练标签b,alphas = smoRand(x, y, 0.6, 0.001, 40)w = get_w(x, y, alphas)print('w : ',w)print('b : ',b)showDataSet(dataSet,w,b,alphas)

2：smo 优化版本

外层循环遍历训练数据集检验它们是否满足kkt条件，不满足则更新，

在遍历所有满足 0<aplas<C的样本点，(支持向量) 是否满足kkt条件，不满足则更新

import numpy as npimport matplotlib.pyplot as plt# 产生一个线性可分的数据集def makeLinearSeparableDateSet(NormalVector,numpoints=100):    """    NormalVector : 是一个列表，存储的是产生随机数据那条的直线的法向量    numpoints : 模拟数据集中的数据点个数    Randomly generate numlines points on both sides of the    hyperplane :  NormalVector * x  =0    notice: NormalVector and x are vectors    return  a linear Separable data set .    """    w = np.array(NormalVector)      # w ：vector 法向量的垂线    numFeatures = len(NormalVector) #  产生每条数据 特征的数量，几个特征    dataSet = np.zeros((numpoints,numFeatures+1)) #产生一个全0 矩阵 ,numFeatures  +1是标签    for i in range(numpoints):        x = np.random.rand(1,numFeatures) # 产生 1*numFeatures 符合N(0,1)        x = x*20-10        innerProduct = np.sum(w*x)     # 注意w*x是叉乘，不是矩阵乘法        if innerProduct <=0 :          # w*x <0 ，负分类点            dataSet[i] = np.append(x,-1)        else :            dataSet[i] = np.append(x,1)    return dataSet# 训练的所有参数，封装到一个paramaters_All 类中，方便各个函数操作class parameters_All:    def __init__(self,x,y,C,toler):         self.x = x  # 训练数据        self.y = y  # 标签        self.C = C  #  松弛变量        self.toler = toler  #容错率         self.m  = np.shape(x)[0]  # 训练数据个数        self.alphas = np.mat(np.zeros((self.m,1))) #初始化参数alphas 为0        self. b = 0  # 初始化参数 b 为  0        self.ecache = np.mat(np.zeros((self.m,2))) # 误差缓存，初始化为0 第一列为标准位，1代表实际误差# 随机选择一个样本点 j  def selectJ_rand(i,m):    """     i: 样本点 i 索引 下标     m:  样本总数     return : 在 m 范围内返回一个与 i 不同的索引下标    """    j = i    while j==i:        j = int(np.random.uniform(0,m))    return j#计算 样本点误差def get_E(parameters_All,i):    """    parameters_all: 所有的参数    i : 样本点 i 的索引下标    return : E 误差，预测值与实际值差  公式：Ei= w*x +b -yi= ( alphas*y*x*x[i,:]+b-yi)    """    x = parameters_All.x    y = parameters_All.y    b = parameters_All.b    alphas = parameters_All.alphas    E = float(np.multiply(alphas,y).T*(x*x[i,:].T)) + b -y[i]    return E# 启发式选择Ej,使得abs(Ei - Ej) 最大 ，否则就随机返回一个Ejdef selectJ_Inspire(parameters_All,i,Ei):    """    parametrs_All : 所有参数    i : 样本点i索引下标    Ei: 样本点i 的误差     return : j ,Ej  此时的abs(Ej - Ei) 最大    """       m = parameters_All.m       maxE = 0     # 记录误差最大值    max_index = -1  #记录与 abs(Ei -Ej)误差最大的这个样本的下标    Ej = 0   #与Ei 相对应的Ej    parameters_All.ecache[i] = [1,Ei]  # 将i这个样本点写入误差缓存记录表    validEchaeIndex = np.nonzero(parameters_All.ecache[:,0].A)[0] #将误差缓存表中的有实际记录的误差的下标提取出来     if len(validEchaeIndex) > 1: #缓存表中有记录        for k in validEchaeIndex:            if k == i:                continue            Ek =get_E(parameters_All,k)            if abs(Ei -Ek) > maxE:                maxE = abs(Ei-Ej)                max_index = k                Ej = Ek        return max_index ,Ej    else: #误差缓存记录表中没有记录，就随机在总样本中选择一个样本点        j = selectJ_rand(i,m)        Ej = get_E(parameters_All,j) #求得这个样本点的误差    return j,Ej#更新误差缓存表def updateEk(parameters_All,k):    """    parameters_ALL : 所有参数    k:  下标索引    """    Ek = get_E(parameters_All,k)    parameters_All.ecache[k] = [1,Ek]    # alpha 的修剪函数def clipAlpha(alapha_new, H ,L ):    """    alpha_new : 更新的aplha    H：alpha 的上界    L：alpha 的下界    Return : 修剪后的alpha    """    if alapha_new > H :        alapha_new = H    if L >alapha_new:        alapha_new  = L    return alapha_new# smo 参数 i 更新函数def smoOptimizer(parameters_All,i):    """    parameters_All : 所有参数    i ：样本点 i 的下标    return：alpha[i]是否更新 ，if 更新 return 1 ，else : return 0    """    x = parameters_All.x  # 训练数据     y = parameters_All.y  # 训练数据的标签    toler =parameters_All.toler  #容错率    alphas = parameters_All.alphas      C = parameters_All.C  #松弛变量    Ei = get_E(parameters_All,i) # 样本点i 的误差    # 不满足kkt条件    if ((y[i]*Ei < -toler) and (alphas[i] < C)) or ((y[i]*Ei > toler) and (alphas[i] > 0)):        j ,Ej =selectJ_Inspire(parameters_All,i,Ei) #找出 abs(Ej -Ei) 的样本点        #保存更新前的aplpha值，使用深拷贝        alphaIold = alphas[i].copy()        alphaJold = alphas[j].copy()        #计算上下界L和H        if (y[i] != y[j]): # yi == yj             L = max(0, alphaJold - alphaIold)            H = min(C, C + alphaJold - alphaIold)        else:        #yi!=yj            L = max(0, alphaJold +alphaIold - C)            H = min(C,  alphaJold +alphaIold)        if L== H :# 当上下界相同时，不满足条件            return 0         #计算eta k11 + k22 -2k12        eta =  x[i,:]*x[i,:].T + 1.0*x[j,:]*x[j,:].T-2.0 * x[i,:]*x[j,:].T        if eta <= 0:            return 0   # 除数不能为0          #更新alpha[j]        alphas[j] = alphaJold+y[j]*(Ei - Ej)/eta        #修剪alphas[j]        parameters_All.alphas[j] =clipAlpha(alphas[j],H,L)        #更新Ej至误差缓存        updateEk(parameters_All,j)        if (abs(parameters_All.alphas[j] - alphaJold) < 0.00001):  #alpha_j变化太小,跳出这次循环            return 0           #更新alpha[i]        #公式  alphaIold =C*yi -alphaJold*yiyj    alpha[i]_new = c*yi -alpha[j]_new*yiy2j 两个式子相减        parameters_All.alphas[i] += y[j]*y[i]*(alphaJold - parameters_All.alphas[j])        #更新Ei至误差缓存        updateEk(parameters_All,i)        #更新b1和b2        b1 = parameters_All.b - Ei- y[i]*(parameters_All.alphas[i]-alphaIold)*x[i,:]*x[i,:].T - y[j]*(parameters_All.alphas[j]-alphaJold)*x[i,:]*x[j,:].T        b2 = parameters_All.b - Ej- y[i]*(parameters_All.alphas[i]-alphaIold)*x[i,:]*x[j,:].T - y[j]*(parameters_All.alphas[j]-alphaJold)*x[j,:]*x[j,:].T        #根据b1和b2更新 b        if (0 < alphas[i]) and (C > alphas[i]):            parameters_All.b = b1        elif (0 < alphas[j]) and (C > alphas[j]):            parameters_All.b = b2        else:            parameters_All.b = (b1 + b2)/2.0        return 1    else :  # 样本点 i 满足kkt条件        return 0#smo 训练函数def smo_F(x,y,C,toler,epochs):    """    x: 训练数据    y: 训练数据标签    C：松弛变量     toler: 容错率      epochs: 训练批数    return :最优化W*, b*,alphas*     """    x = np.mat(x)    y = np.mat(y).transpose()    para_All = parameters_All(x,y,C,toler) # 将所有数据封装到一个类中，方便各个函数调用    epoch = 0    entireSet = True #是否    alphaChanged = 0 # alphas 中的改变次数    while (epoch <epochs and alphaChanged >0) or entireSet:        alphaChanged = 0        if entireSet:# 遍历整个训练数据集            for i in range(para_All.m):                alphaChanged+= smoOptimizer(para_All,i)# 样本点i是否满足kkt条件，不满足更新，t=1,满足t=0            epoch+=1 #训练轮数加 1        else :            #在误差范围内检查支持向量是否满足kkt条件  0<alphas<C 这个点就是支持向量             supportVecIndex =  np.nonzero((para_All.alphas.A > 0) * (para_All.alphas.A < C))[0] #找出支持向量的下标            for  i in supportVecIndex:                alphaChanged += smoOptimizer(para_All,i)# 当支持向量不满足kkt条件+1，否则+0            epoch +=1 #训练次数+1        if (alphaChanged == 0): #当alphas还在改变，未找到决策面，继续训练            entireSet = False        else:            entireSet = True    #计算 W*             alphas= np.array(para_All.alphas)    x = np.array(x)    y = np.array(y).reshape(1, -1).T # 将y 变成 m*1 [y]    res =np.tile(y,(1, 2)) * x #np.title,将y 扩展成 m*2 [y,y]    w = np.dot(res.T, alphas)    return w.tolist(),para_All.b ,para_All.alphas#训练结束后图像可视化def showDataSet(dataSet,w,b,alphas):    ax = plt.subplot(1,1,1,facecolor='white')    ax.set_title("SVM")    plt.xlabel('X')    plt.ylabel('Y')    labels = dataSet[:,2]         # 获得 数据集的标签    idx_1 = np.where(dataSet[:,2] == 1 )  # 找出数据集中标签为 1 的下标    p1 = ax.scatter(dataSet[idx_1,0],dataSet[idx_1,1],marker='o',color='g',label=1,s=20)    idx_2 = np.where(dataSet[:,2] == -1)    p2 = ax.scatter(dataSet[idx_2,0],dataSet[idx_2,1],marker='x',color='r',label=-1,s=20)    #绘制决策面直线    data=dataSet[:,0:2]    x1 = max(data[:,0])    x2 = min(data[:,0])    a1, a2 = w    b = float(b)    a1 = float(a1[0])    a2 = float(a2[0])    y1, y2 = (-b- a1*x1)/a2, (-b - a1*x2)/a2    plt.plot([x1, x2], [y1, y2])    #找出支持向量点    for i, alpha in enumerate(alphas):        if abs(alpha) > 0:            x, y = data[i]            plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')    plt.legend(loc = 'upper right')    plt.show()# 测试代码 dataSet = makeLinearSeparableDateSet([3,4],15)x = dataSet[: ,0:2]  # 训练数据y = dataSet[: ,-1]   # 训练标签w,b,alphas = smo_F(x,y,0.6,0.0001,50)showDataSet(dataSet,w,b,alphas)

import numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom matplotlib import stylefrom sklearn.svm import SVC# 产生一个线性可分的数据集def makeLinearSeparableDateSet(NormalVector,numpoints=100):    """    NormalVector : 是一个列表，存储的是产生随机数据那条的直线的法向量    numpoints : 模拟数据集中的数据点个数     Randomly generate numlines points on both sides of the    hyperplane :  NormalVector * x  =0    notice: NormalVector and x are vectors    return  a linear Separable data set .    """    w = np.array(NormalVector)      # w ： vector 法向量的垂线    numFeatures = len(NormalVector) #  产生每条数据 特征的数量，几个特征    dataSet = np.zeros((numpoints,numFeatures+1)) #产生一个全0 矩阵 ,numFeatures  +1是标签    for i in range(numpoints):        x = np.random.rand(1,numFeatures) # 产生 1*numFeatures 符合N(0,1)        x = x*20-10        innerProduct = np.sum(w*x)     # 注意w*x是叉乘，不是矩阵乘法         if innerProduct <=0 :          # w*x <0 ，负分类点            dataSet[i] = np.append(x,-1)        else :            dataSet[i] = np.append(x,1)    return dataSetdata=makeLinearSeparableDateSet((3,4),50)x = data[:,0:2]y = data[:,2]plt.rcParams['figure.figsize'] =(12,6)#print(plt.style.available)# 获取所有的自带样式#style.use('fivethirtyeight') # 使用自带的样式进行美化def draw_svm(x,y,C=1.0):    #plotting the points    plt.scatter(x[:,0],x[:,1],c=y)    # the svm model with given C parameter   # clf = SVC(kernel='linear',C=C)    clf = SVC(kernel='poly',C=C)    clf_fit = clf.fit(x,y)    #Limit of the axes    ax = plt.gca()    xlim = ax.get_xlim()    ylim = ax.get_ylim()    #Creating the meshgrid    xx = np.linspace(xlim[0],xlim[1],200)    yy = np.linspace(ylim[0],ylim[1],200)    YY ,XX =np.meshgrid(yy,xx)    xy = np.vstack([XX.ravel(),YY.ravel()]).T    Z = clf.decision_function(xy).reshape(XX.shape)     #plotting the boundary    ax.contour(XX,YY,Z,colors='k',levels=[-1,0,1],alpha=0.5,linestyles=['--','-','--'])#等高线    ax.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],s=100,linewidth=1,facecolors='red')    plt.show()draw_svm(x,y,1)