力扣第20题记录

一、题目：20. 有效的括号

二、题目解析：

题目解析：该题需要用到数据结构当中的stack栈 （特点：后进先出）
解题步骤：

1. 创建一个HashMap,把括号配对放进去，维护匹配关系,{“(”:“)”}
2. 创建一个stack,for循环遍历字符串，对于每一个字符，如果map里有这个key,那说明它是一个左括号,从map里取得相对应的右括号
   （为什么？）因为计算机不知道这些括号配对关系，需要我们自己处理,把它push进stack里。
   否则的话，它就是右括号，需要pop出stack里的第一个字符，然后看它是否等于当前的字符。如果不相符，则返回false
3. 循环结束后，如果stack不为空，说明还剩一些左括号没有被闭合，返回false。否则返回true。

图示帮助理解：

三、代码如下：

public boolean isValid(String s){
        Map<Character,Character> map = new HashMap<Character, Character>(16);
        map.put('(',')');
        map.put('[',']');
        map.put('{','}');
        Stack<Character> stack = new Stack<Character>();
        for (int i = 0; i < s.length(); i++) {
            char c = s.charAt(i);
            if(map.containsKey(c)){
                stack.push(map.get(c));
            }else{
                if(stack.size() == 0 || stack.pop() != c){
                    return false;
                }
            }
        }
        // 遍历完栈里面还有元素，说明还有没匹配的元素，则返回false
        if(stack.size() != 0){
            return false;
        }
        return true;
    }

四、测试

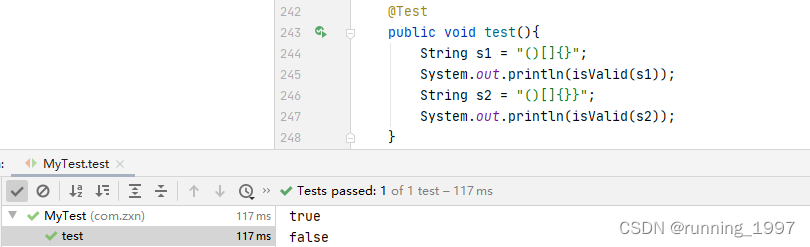
五、结束