算法笔记-递归

最新推荐文章于 2021-07-19 12:57:14 发布

原创最新推荐文章于 2021-07-19 12:57:14 发布 · 289 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#递归 #回溯

JAVA数据结构专栏收录该内容

12 篇文章

订阅专栏

本文详细探讨了递归的概念，解释了递归与栈的关系，强调了递归的重要规则，并展示了递归在解决数学问题和算法中的应用。递归可用于8皇后问题、汉诺塔等，但在实现时需要注意避免堆栈溢出和重复计算。通过数据结构优化，可以有效避免重复计算，提高效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一.什么是递归(recursive) 回溯

1.简单的说: 递归就是方法自己调用自己,每次调用时传入不同的变量.递归有助于编程者解决复杂的问题,同时可以让代码变得简洁。

去的过程叫递,回来的过程叫归.

递归本身就是借助栈来实现的

2.图解方式说明了递归的调用机制:

3.递归需要遵守的重要规则(这个很重要这个搞不清楚递归调用几次就蒙了)

1) 执行一个方法时，就创建一个新的受保护的独立空间(栈空间)

2) 方法的局部变量是独立的，不会相互影响, 比如 n 变量

3) 如果方法中使用的是引用类型变量(比如数组)，就会共享该引用类型的数据.

4) 递归必须向退出递归的条件逼近，否则就是无限递归,出现 StackOverflowError，死龟了:)

5) 当一个方法执行完毕，或者遇到 return，就会返回，遵守谁调用，就将结果返回给谁，同时当方法执行完毕或

者返回时，该方法也就执行完毕

public static void test(int n) {

//打印
if (n > 2) {

test(n - 1); } //else {
System.out.println("n=" + n);

// }

}

//阶乘问题

public static int factorial(int n) {

if (n == 1) {

return 1;

} else {

return factorial(n - 1) * n; // 1 * 2 * 3

}

}
 

 
}

二：递归与栈的关系

常常听到 “递归的过程就是出入栈的过程”，这句话怎么理解？我们以上述代码为例，取 n=3，则过程如下：

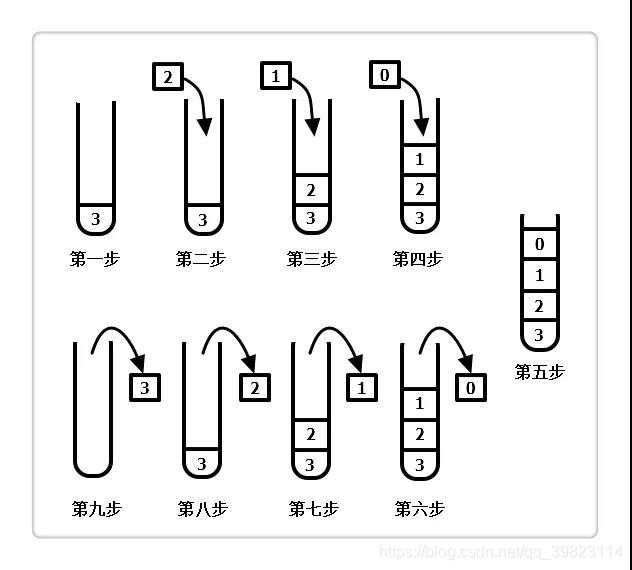
第 1~4 步，都是入栈过程，Factorial(3)调用了Factorial(2)，Factorial(2)又接着调用Factorial(1)，直到Factorial(0)；

第 5 步，因 0 是递归结束条件，故不再入栈，此时栈高度为 4，即为我们平时所说的递归深度；

第 6~9 步，Factorial(0)做完，出栈，而Factorial(0)做完意味着Factorial(1)也做完，同样进行出栈，重复下去，直到所有的都出栈完毕，递归结束。

每一个递归程序都可以把它改写为非递归版本。我们只需利用栈，通过入栈和出栈两个操作就可以模拟递归的过程，二叉树的遍历无疑是这方面的代表。

但是并不是每个递归程序都是那么容易被改写为非递归的。某些递归程序比较复杂，其入栈和出栈非常繁琐，给编码带来了很大难度，而且易读性极差，所以条件允许的情况下，推荐使用递归。

三递归能做什么

1) 各种数学问题如: 8 皇后问题 , 汉诺塔, 阶乘问题, 迷宫问题, 球和篮子的问题(google 编程大赛)

2) 各种算法中也会使用到递归，比如快排，归并排序，二分查找，分治算法等.

3) 将用栈解决的问题-->第归代码比较简洁

四.实现Demo

八皇后问题:

package com.nmys.story.Recursive;

/**
 * @Auther: Jia
 * @Date: 2019/8/18 20:12
 * @Description:
 */
public class Queue8 {

    //定义一个max表示共有多少个皇后
    int max = 8;
    int[] array = new int[max];
    static int count = 0;
    static int judgeCount = 0;
    public static void main(String[] args) {

         Queue8 queue8 = new Queue8();
         queue8.check(0);
         System.out.printf("一共有%d解法", count);
        System.out.println();
        System.out.printf("一共判断冲突的次数%d次", judgeCount); // 1.5w



    }


    //编写一个方法，放置第n个皇后
    //特别注意： check 是 每一次递归时，进入到check中都有
    // for(int i = 0; i < max; i++)，因此会有回溯
    private  void check(int n){
        //n = 8 , 其实8个皇后就既然放好
         if(n == max){
             print();
             return;
         }
         //依次放入皇后, 并判断是否冲突
        for (int i = 0; i <max ; i++) {
            //n代表第几个皇后 i代表放入的位置,即改行的第i列
            array[n] = i;
            // 不冲突进入judge()方法
            if(judge(n)){
                //接着放n+1个皇后,开始递归
                check(n+1);
            }
            //如果冲突，就继续执行 array[n] = i;

        }
    }



    //检测当前摆放的皇后的位置是否与前面已经摆放的皇后的位置有冲突
    private  boolean judge(int n){
        judgeCount++;
        for (int i = 0; i <n ; i++) {
            //1. array[i] == array[n]  表示判断 第n个皇后是否和前面的n-1个皇后在同一列
            //2. Math.abs(n-i) == Math.abs(array[n] - array[i]) 表示判断第n个皇后是否和第i皇后是否在同一斜线
            // n = 1  放置第 2列 1 n = 1 array[1] = 1
            // Math.abs(1-0) == 1  Math.abs(array[n] - array[i]) = Math.abs(1-0) = 1
            //3. 判断是否在同一行, 没有必要，n 每次都在递增
            if(array[i] == array[n]||Math.abs(n-i) == Math.abs(array[n] - array[i]))
                    return false;
        }
        return true;
    }



    //写一个方法,可以将皇后摆放的位置输出
    private void print(){
        count++;
        for (int i = 0; i <array.length ; i++) {
             System.out.printf(array[i]+" ");
        }
        System.out.println();
    }

}

迷宫问题:

package com.nmys.story.Recursive;

/**
 * @Auther: Jia
 * @Date: 2019/8/18 07:52
 * @Description:
 */
public class RecursiveDemo {

    public static void main(String[] args) {
        test(4);
        //先创建一个二维数组,模拟迷宫
        int[][] map = new int[8][7];
        //使用1表示墙
        //上下全部置为1
        for (int i = 0; i <7 ; i++) {
            map[0][i] = 1;
            map[7][i] = 1;
        }
        // 左右全部置为1
        for (int i = 0; i <8 ; i++) {
            map[i][0] = 1;
            map[i][6] = 1;
        }
        //设置挡板, 1 表示
        map[3][1] = 1;
        map[3][2] = 1;
        map[1][2] = 1;
		map[2][2] = 1;
        //输出地图
        System.out.println("地图的情况");
        for (int i = 0; i <8 ; i++) {
            for (int j = 0; j <7 ; j++) {
                 System.out.print(map[i][j] + " ");

            }
                 System.out.println();
        }
        //使用递归回溯找出路
        findWay(map,1,1);
        //输出新的地图, 小球走过，并标识过的递归
        System.out.println("小球走过，并标识过的 地图的情况");
        for (int i = 0; i <8 ; i++) {
            for (int j = 0; j <7 ; j++) {
                System.out.print(map[i][j] + " ");

            }
            System.out.println();
        }
    }

    //打印问题
    public static void test(int n){
        if(n>2){
            test(n-1);
        }else{
            System.out.println("n="+n);

        }
    }

    //使用递归回溯来给小球找路
    //说明
    //1. map 表示地图
    //2. i,j 表示从地图的哪个位置开始出发 (1,1)
    //3. 如果小球能到 map[6][5] 位置，则说明通路找到.
    //4. 约定： 当map[i][j] 为 0 表示该点没有走过 当为 1 表示墙  ； 2 表示通路可以走 ； 3 表示该点已经走过，但是走不通
    //5. 在走迷宫时，需要确定一个策略(方法) 下->右->上->左 , 如果该点走不通，再回溯
    /**
     *
     * @param map 表示地图
     * @param i 从哪个位置开始找
     * @param j
     * @return 如果找到通路，就返回true, 否则返回false
     */
    public static boolean findWay(int[][] map ,int i, int j){
        if(map[6][5]== 2){
            return true;
        }else{
            if(map[i][j] == 0){
                map[i][j] = 2; // 假定该点是可以走通.
                if(findWay(map,i+1,j)){ //向下走
                    return true;
                }else if(findWay(map,i,j+1)){ //向右走
                    return  true;
                }else if(findWay(map,i-1,j)){ //向上
                    return  false;
                }else if(findWay(map,i,j-1)){ // 向左走
                    return true;
                }else{
                    //说明该点是走不通，是死路
                    map[i][j] = 3;
                   return false;
                }


            }else{
                return false;
            }
        }
    }



}

五.注意问题

1.递归代码要警惕堆栈溢出

2..递归代码要警惕重复计算

整个递归过程分解一下的话，那就是这样的：

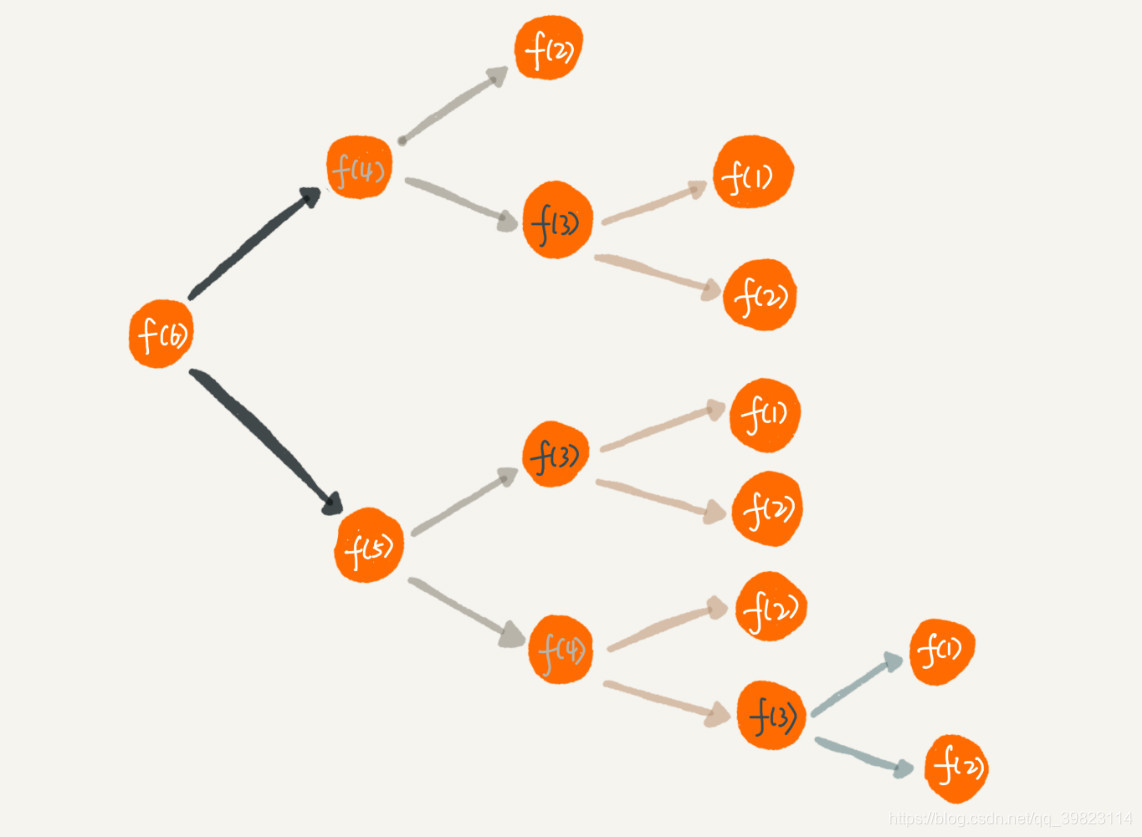
可以优化下:

可以通过一个数据结构（比如散列表）来保存已经求解过的 f(k)。当递归调用到 f(k) 时先看下是否已经求解过了

public int f(int n) {
  if (n == 1) return 1;
  if (n == 2) return 2;
  
  // hasSolvedList 可以理解成一个 Map，key 是 n，value 是 f(n)
  if (hasSolvedList.containsKey(n)) {
    return hasSovledList.get(n);
  }
  
  int ret = f(n-1) + f(n-2);
  hasSovledList.put(n, ret);
  return ret;
}